Навигация
1. ХАОС
Их либе жизнь и обожаю хаос...
И.Бродский, "Два часа в резервуаре"
1.1 Классический динамический хаос: неустойчивость по начальным условиям
Хаотическое поведение может возникать даже в очень простых системах, например, из физических моделей – в колебаниях сферического маятника с двумя степенями свободы. Мы для начала рассмотрим даже ещё более простые математические модели с дискретным временем – сдвиг Бернулли и преобразование пекаря.
Сдвиг Бернулли представляет собой отображение в одномерном пространстве на интервале (0,1) по закону
xn+1=2xn(mod1).
Это уравнение движения детерминистично: по заданному xn однозначно вычисляется xn+1. При этом, однако, сдвиг Бернулли не является обратимым отображением. Симметрия во времени нарушена ещё на уровне уравнения движения. Этим сдвиг Бернулли отличается от динамических систем с обратимыми уравнениями движения.
Сдвиг Бернулли представляет собой пример детерминистического хаоса. Можно представить примеры последовательностей, начинающихся с какого-нибудь произвольного числа, например:
{0.13; 0.26; 0.52; 0.04; 0.08; 0.16; 0.32; 0.64; 0.28... }
и
{0.14; 0.28; 0.56; 0.12; 0.24; 0.48; 0.96; 0.92; 0.84... } –
как видим, незначительное отличие в начальных условиях уже на 4-м шаге порождает существенное различие траекторий, а в дальнейшем их поведение совершенно различно.
Легко показать, что со временем разойдутся траектории любых двух сколь угодно близких точек. Запишем число x в виде двоичной дроби:
x=0.u–1u–2u–3...u–k...=u–1/2 + u–2/22 + u–3/23 + ... + u–k/2k + ...
Описанное выше отображение соответствует сдвигу u–k'=u–(k+1) , откуда становится понятным название "сдвиг Бернулли". Видно, что нулевой разряд числа при этом теряется, что соответствует не-взаимооднозначности отображения.
Описание эволюции динамической системы типа сдвига Бернулли в терминах траектории неадекватно, так как для адекватности траектория должна оставаться "почти одной и той же" при незначительном изменении начальных условий.
В данном же случае имеет смысл обратиться к статистическому описанию, введя плотность вероятности r(x) пребывания системы в каждой точке x интервала (0,1). Отображение представляет собой оператор U, действующий на эту функцию:
rn+1=Urn(x)= ( rn(x/2)+rn((x+1)/2) ) / 2.
Оказывается, что при многократном применении оператора отображения к произвольному распределению плотности вероятности оно стремится к константе:
rn=Unr0(x)®rµ(x)=const.
В дальнейшем мы ещё вернемся к отображению Бернулли и свойствам его оператора, а пока рассмотрим другую простую динамическую систему, теперь уже двумерную, называемую преобразованием пекаря:
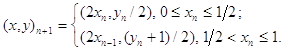
Правило, определяющее преобразование пекаря, очень просто. Сначала квадрат со стороной, равной 1, сплющивается в прямоугольник длиной 2 и высотой 1/2, затем правая половина полученного прямоугольника накладывается на левую, образуя новый квадрат. Процесс в чём-то аналогичен размешиванию теста, отсюда и название.
В отличие от сдвига Бернулли преобразование пекаря обратимо во времени. Однако оно точно так же порождает хаотическое движение, связанное с неустойчивостью по начальным условиям.
Преобразование пекаря сводится к сдвигу в двусторонней двоичной последовательности:
x0y = ....u–k...u–3u-2u–1u0u1u2...uk....,
uk' = u–(k+1).
Видно, что при этом никакие двоичные разряды не теряются, что и соответствует обратимости преобразования пекаря во времени.
Аналогично сдвигу Бернулли, преобразование пекаря порождает динамический хаос, и описание движения точки в терминах траекторий также неадекватно.
В случае преобразования пекаря описание эволюции системы в статистических терминах даже более "физически осмысленно", чем для сдвига Бернулли. Дело в том, что теперь, в двумерном случае, можно рассматривать координатную плоскость как фазовое пространство некоторой динамической системы с одной степенью свободы: ось x соответствует координате, а ось y – импульсу. Аналогия с "физическими" динамическими системами усиливается ещё и тем, что выполняется теорема Лиувилля: сохраняется объём в фазовом пространстве. Другими словами, взяв ансамбль точек внутри некоторой области и проделав произвольное количество преобразований пекаря, мы обнаружим тоже самое количество точек внутри некоторой другой области (форма её при этом очень сильно изменится и станет крайне замысловатой). Объём этой области (в нашем двумерном случае ему соответствует площадь) останется неизменным.
Несмотря на обратимость преобразования пекаря во времени, эволюция при t ® +µ и при t ® –µ оказывается различной [1,c.114].
Кроме описанных выше, существует ещё много сравнительно простых моделей динамического хаоса. Однако мы воздержимся от их подробного рассмотрения, и перейдём теперь к причинам, лежащим в основе непредсказуемого поведения физических систем.
Похожие работы
... рассеянным в пространстве вследствие спонтанного рассеяния атомов по объему сосуда. Каждый атом обладает кинетической энергией, и потому распространение атомов по сосуду приводит и к распространению энергии. 1.3 Хаос и порядок В химии, как и в физике, все естественные изменения вызваны бесцельной “деятельностью” хаоса. Мы познакомились с двумя важнейшими достижениями Больцмана: он установил, ...
... более ясно осознать свое место в общенаучных коллизиях нашего времени. В частности, это касается проблемы взаимодействия "классического" и "неклассического" научного разума, определяющую всю макродинамику современной науки . Необходимо осознать, что внутренние теоретические коллизии музыкознания имеют прямое отношение к глобальной эволюции методов познания, используемых человеком. В частности, ...
... ограниченного числа явлений: механика Ньютона, или далеко не оптимальным или совершенным творением техники: лайнер "Титаник", самолеты Ту-144, "Конкорд", Чернобыльская АЭС, космические корабли серии " Шаттл" и многое-многое другое. 3. Развитие системного подхода в науке 3.1 Ранние попытки систематизации физических знаний Первой действительно успешной попыткой систематизации знаний о ...
... , энтропия — не просто безостановочное соскальзывание системы к состоянию, лишенному какой бы то ни было организации. При определенных условиях энтропия становится прародительницей порядка. ПОРЯДОК И ХАОС От порядка к хаосу В физической картине мира до 70-х годов XX века царствовали два закона классической термодинамики. Первый закон термодинамики (закон сохранения и превращения энергии) ...

0 комментариев