Навигация
Статистическое описание. Диссипативный хаос
1.3 Статистическое описание. Диссипативный хаос
Можно описывать мир в терминах траекторий (в классической физике) или волновых функций (в квантовой механике). Почти сто лет назад Гиббс и Эйнштейн ввели ещё один тип описания – статистическое описание в терминах ансамблей. Описание отдельной динамической системы заменяется описанием ансамбля систем, которые все соответствуют одному и тому же гамильтониану и различаются только начальными условиями эволюции. Для введения ансамблевой точки зрения были две основные причины. Во-первых, описание в терминах ансамбля позволило удобно вычислять средние значения. Во-вторых, понятие ансамбля стало необходимым для описания системы, достигшей термодинамического равновесия. Оказалось, что термодинамические свойства можно понять только в терминах ансамблей, но отнюдь не в терминах отдельных траекторий или волновых функций. Ансамблевый подход применим ко всем динамическим системам, интегрируемым и неинтегрируемым, устойчивым и неустойчивым.
Основной величиной в ансамблевом подходе становится распределение вероятностей. Однако ничто не мешает вернуться как к предельному случаю. Подход Гиббса–Эйнштейна – альтернативный, но эквивалентный способ представления законов физики, он является сводимым статистическим описанием.
Концепцию несводимых статистических описаний, развиваемую школой И.Пригожина, мы подробнее рассмотрим в третьем разделе. Пока что вкратце обратимся к классическому диссипативному хаосу, для которого статистическое описание является единственно возможным подходом. Введём также некоторые понятия, необходимые для дальнейших рассуждений о статистическом описании. (Подробнее – см. [4]).
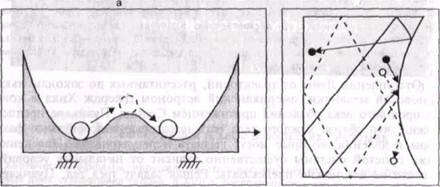
Как и прежде, каждому состоянию системы соответствует точка в фазовом пространстве. Но в теории ансамблей Гиббса система как целое представима лишь "облаком" точек в фазовом пространстве. Это "облако" описывается непрерывным распределением плотности вероятности r(q1,...,qs,p1,...,ps) в фазовом пространстве. Каждая точка фазового пространства движется во времени по своей динамической траектории, которые никогда не пересекаются. Две первоначально различные точки навсегда остаются различными. Это фундаментальное свойство приводит к теореме Лиувилля, которая уже упоминалась при описании преобразования пекаря. Эта теорема утверждает, что плотность r ведёт себя как несжимаемая жидкость: для любой динамической системы объём области, занятой представляющими точками в фазовом пространстве, сохраняется в ходе эволюции. Однако теорема Лиувилля отнюдь не исключает изменения формы области, занятой представляющими точками.
Вернёмся к хаосу. Примеры хаотически ведущих себя динамических систем, описанные выше, относительно новы и, как уже упоминалось, не всегда "физичны". Термодинамика же и статистическая физика примерно на сто лет раньше столкнулись с проблемой хаотического поведения систем.
За примерами далеко ходить не следует – окружающая нас атмосфера ведёт себя вполне хаотически, предсказание прогноза погоды на сколько-нибудь большой срок – задача огромной сложности (хотя в принципе и небезнадёжная).
Однако даже в атмосфере встречаются относительно устойчивые образования и на некотором уровне описания поведение атмосферы не совсем хаотично. Другим примером того, что (термодинамический) хаос и беспорядок – в физике не синонимы, являются широко известные ячейки Бенара (настолько известные, что автор почему-то совершенно не желает в очередной раз давать описание этого явления – см., например, [1, с.68]). И ячейки Бенара, и атмосферные вихри, и многие другие подобные явления относятся к так называемым диссипативным структурам – структурам, существование которых напрямую обусловлено наличием в системе процессов диссипации энергии и производства энтропии.
Таким образом, простое и сложное, детерминированное и хаотическое поведение сосуществуют в современной физике рядом. Закончим этот очень краткий обзор словами И.Пригожина [1, с.59]: "...хотелось бы подчеркнуть замечательный дуализм, который мы обнаруживаем в природе, – сосуществование равновесных ситуаций типа излучения абсолютно чёрного тела и высокоорганизованных объектов, одним из наиболее замечательных среди которых, по-видимому, является человеческий мозг с его 1011 связанных между собой нейронами. Порядок и беспорядок не могут быть поняты в терминах Больцмана: порядок как менее вероятное состояние, беспорядок как более вероятное состояние. И порядок, и беспорядок являются неотъемлемыми составными частями и продуктами коррелированных эволюционных процессов".
2. НЕОБРАТИМОСТЬ ВРЕМЕНИ
Меж тем вот палец твой, он на пульсе. А вот часы,
Они идут, и довольно быстро – я проверял...
М.Щербаков, "Фармацевт"
2.1 Обратимость времени в классической и квантовой механике
Центральная тема размышлений И.Пригожина и направление размышлений "брюссельской школы" состоит в решении дилеммы: отрицание – неотрицание стрелы времени. Выражение "стрела времени" было введено в 1928 г. Эддингтоном в его книге "Природа физического мира". В этой книге Эддингтон предсказывал конец господства в физике "первичных" (детерминистических) законов и наступление эры "вторичных" (статистических) законов, описывающих необратимые процессы.
В том виде, в каком время входит в фундаментальные законы физики от классической динамики до теории относительности и квантовой физики, время не содержит в себе различия между прошлым и будущим. Для многих физиков это уже почти вопрос веры: до тех пор и поскольку речь идёт о фундаментальном уровне описания, "стрелы времени" не существует.
Но на макроуровне, в мире объектов, с которыми мы имеем дело ежедневно, на уровне живых организмов необратимость времени сомнений ни у кого не вызывает. Процессы старения, распада, рассеяния энергии неизбежны. Как сказано в пародии на известную песню, "фарш невозможно провернуть назад". Стрела времени на самом деле присутствует и во всех физических теориях, описывающих реальный мир. Но присутствует она там не в виде членов в уравнениях, а в виде примечаний и комментариев к этим уравнениям, представляя собой высказывания типа: "...Из этих двух решений мы должны выбрать первое, поскольку оно соответствует прямому направлению хода времени" или "...В формуле (...) первый член отвечает за прямое, а второй – за обратное рассеяние, в реальности не наблюдающееся, поэтому мы будем рассматривать только решения вида (...)".
В более явном виде стрела времени появляется в термодинамике, в различных формулировках её второго начала и в H-теореме Больцмана. Удивительным оказывается то, что при попытке анализировать такие процессы, как диффузия или вязкость – вполне макроскопически необратимые – физика успешно их описывает с помощью обратимых во времени микропроцессов.
В основе классической механики (исторически, даже если и не логически) лежит закон Ньютона. Он обратим во времени и детерминистичен. Закон Ньютона можно рассматривать как прототип некоего Универсального Закона Природы.
Понятие закона природы заслуживает некоторого отступления. Мы настолько привыкли к нему, что оно воспринимается как нечто само собой разумеющееся. Однако в других взглядах на мир (не всегда вполне научных – с нынешней точки зрения) такая концепция "закона природы" отсутствует. По Аристотелю, живые существа не подчиняются никаким законам, их деятельность обусловлена их собственными внутренними причинами. Каждое существо стремится к достижению своей собственной истины. В Китае господствовали взгляды о спонтанной гармонии космоса, своего рода статистическом равновесии, связывающем воедино природу, общество и небеса. Примеры можно множить и множить...
Идея о том, что в мире могут действовать законы, вызрела в недрах западной мысли. Отчасти она восходит к стоикам, несмотря на ту роль, которую они отводили року. Немаловажную роль, вероятно, сыграли и иудеохристианские представления о Боге как абсолютном Вседержителе, устанавливающем законы для всего сущего. Так или иначе, открытие неизменяющихся детерминистических законов как бы сближало человеческое знание с божественной, вневременной точкой зрения.
Намеченная программа оказалась необычайно успешной. Однако на протяжении всей истории западной мысли неоднократно возникал один и тот же вопрос: как следует понимать новое, играющее центральную роль, в мире, управляемом детерминистическими законами?
Впервые этот вопрос возник задолго до рождения современной науки. Ещё Платон связывал разум и истину с доступом к "бытию", неизменной реальностью, стоящей за "становлением". Становление, поток воспринимаемых нами явлений, относится к сфере "чистого мнения". Однако Платон сознавал парадоксальность такой позиции, поскольку она принижала жизнь и мысль, которые представали как неотделимые от процесса становления. В "Софисте" Платон приходит к заключению, что нам необходимы и бытие, и становление.
С той же трудностью столкнулись и атомисты. Чтобы допустить возникновение нового, Лукрецию пришлось ввести "клинамен", возмущающий детерминистическое падение атомов в пустоте. Обращение к клинамену часто подвергалось критике как введение чужеродного элемента в схему атомистического описания. Но и через два тысячелетия мы встречаем аналогичное утверждение в работе Эйнштейна, посвящённой самопроизвольному испусканию света возбуждённым атомом, где говорится, что "время и направление элементарных процессов определены случайным образом" [6, с.386]
И клинамен, и спонтанное испускание света относятся к событиям, соответствующим вероятностному описанию. События и вероятности требуются и для эволюционного описания, будь то дарвиновская теория эволюции или история человечества. Встаёт вопрос: можно ли пойти дальше, чем Лукреций и Эйнштейн, "добавившие" события к детерминистическим законам? Можно ли видоизменить само понятие физических законов так, чтобы включить в фундаментальное описание природы необратимость, события и стрелу времени?
Для ответа на этот вопрос обратимся сначала к той области физики, которая имеет дело с "наиболее необратимыми" из встречающихся в повседневной жизни системами – а именно, к термодинамике и статистической физике.
Похожие работы
... рассеянным в пространстве вследствие спонтанного рассеяния атомов по объему сосуда. Каждый атом обладает кинетической энергией, и потому распространение атомов по сосуду приводит и к распространению энергии. 1.3 Хаос и порядок В химии, как и в физике, все естественные изменения вызваны бесцельной “деятельностью” хаоса. Мы познакомились с двумя важнейшими достижениями Больцмана: он установил, ...
... более ясно осознать свое место в общенаучных коллизиях нашего времени. В частности, это касается проблемы взаимодействия "классического" и "неклассического" научного разума, определяющую всю макродинамику современной науки . Необходимо осознать, что внутренние теоретические коллизии музыкознания имеют прямое отношение к глобальной эволюции методов познания, используемых человеком. В частности, ...
... ограниченного числа явлений: механика Ньютона, или далеко не оптимальным или совершенным творением техники: лайнер "Титаник", самолеты Ту-144, "Конкорд", Чернобыльская АЭС, космические корабли серии " Шаттл" и многое-многое другое. 3. Развитие системного подхода в науке 3.1 Ранние попытки систематизации физических знаний Первой действительно успешной попыткой систематизации знаний о ...
... , энтропия — не просто безостановочное соскальзывание системы к состоянию, лишенному какой бы то ни было организации. При определенных условиях энтропия становится прародительницей порядка. ПОРЯДОК И ХАОС От порядка к хаосу В физической картине мира до 70-х годов XX века царствовали два закона классической термодинамики. Первый закон термодинамики (закон сохранения и превращения энергии) ...

0 комментариев