Навигация
Анализ функции фильтрационного сопротивления для неустановившегося притока жидкости (газа) к несовершенной скважине
 Министерство общего и профессионального образования РФ
Министерство общего и профессионального образования РФ
Тюменский Государственный Нефтегазовый Университет
Кафедра РЭНиГМ
Реферат«Анализ функции фильтрационного сопротивления для неустановившегося притока жидкости (газа) к несовершенной скважине»
Выполнил студентГруппы НГР-96-1
Принял профессор
Телков А. П.
Тюмень 1999 г.
Рассмотрим функция (F) которая есть функция пяти параметров F=F (f0, rc, h, x, t*), каждый из которых — безразмерная величина, соответственно равная
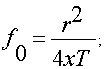

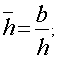

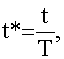 (1)
(1)
где r — радиус наблюдения;
x — коэффициент пьезопроводности;
Т — полное время наблюдения;
h — мощность пласта;
b — мощность вскрытого пласта;
z — координата;
t — текущее время.
Названная функция может быть использована для определения понижения (повышения) давления на забое скважины после ее пуска (остановки), а также для анализа распределения потенциала (давления) в пласте во время работы скважины.
Уравнение, описывающее изменение давления на забое, т. е. при x=h; r=rc или r=rc, имеет вид
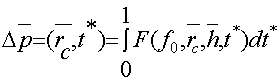 (2)
(2)
где безразмерное значение депрессии связано с размерным следующим соотношением
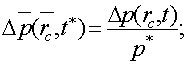 где
где (3)
(3)
здесь Q — дебит;
m — коэффициент вязкости;
k — коэффициент проницаемости.
Аналитическое выражение F для определения изменения давления на забое скважины запишем в виде
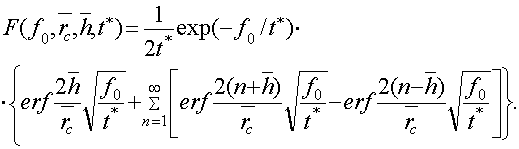 (4)
(4)
Уравнение (2) в приведенном виде не может использоваться для решения инженерных задач по следующим причинам: во-первых, функция (4) сложна и требует табулирования; во-вторых, вид функции исключает возможность выделить время в качестве слагаемого и свести решение уравнения (2) к уравнению прямой для интерпретации кривых восстановления (понижения) давления в скважинах традиционными методами. Чтобы избежать этого, можно поступить следующим образом.
В нефтепромысловом деле при гидродинамических исследованиях скважин широко используется интегрально-показательная функция. Несовершенство по степени вскрытия пласта в этом случае учитывается введением дополнительных фильтрационных сопротивлений (C1), взятых из решения задач для установившегося притока. В соответствии с этим уравнение притока записывается в виде
![]() (5)
(5)
Как видно, дополнительные фильтрационные сопротивления являются функцией геометрии пласта. Насколько верно допущение о возможности использования значений C1(rс, h), пока еще ни теоретически, ни экспериментально не доказано.
Для неустановившегося притока уравнение (2) запишем аналогично в виде двух слагаемых, где в отличие от выражения (5) значения фильтрационных сопротивлений являются функцией трех параметров (rс, h, f0)
![]() (6)
(6)
Как _ видим, дополнительное слагаемое R(rc , h, f0) в уравнении (6) зависит не только от геометрии пласта, но и от параметра Фурье (f0). В дальнейшем будем называть это слагаемое функцией фильтрационного сопротивления. Заметим, что при h=l (скважина совершенная по степени вскрытия) уравнение (2) представляет собой интегрально-показательную функцию
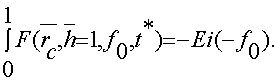 (7)
(7)
С учетом равенства (7) решение (6) запишем в виде
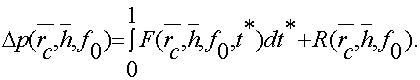 (8)
(8)
Разрешая уравнение (8) относительно функции сопротивления и учитывая уравнение (2), находим
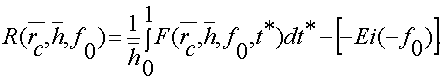 (9)
(9)
и на основании равенства (7) приведем выражение (9) к виду
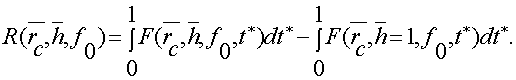 (10)
(10)
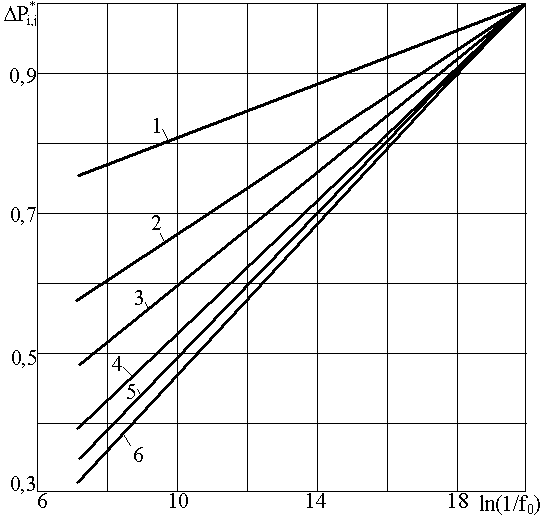
Численное значение R(rс,h,fo) рассчитано по уравнению (10) на ЭВМ в широком диапазоне изменения параметров rc, h, f0. Интеграл (2) вычислялся методом Гаусса, оценка его сходимости выполнена согласно работе [3]. С учетом равенства (7) вычисления дополнительно проконтролированы по значениям интегрально-показательной функции.
С целью выяснения поведения депрессии и функции сопротивления проанализируем их зависимость от значений безразмерных параметров.
Похожие работы
... . Насколько верно допущение о возможности использования значений C1(rс, h), пока еще ни теоретически, ни экспериментально не доказано. Для неустановившегося притока уравнение (2) запишем аналогично в виде двух слагаемых, где в отличие от выражения (5) значения фильтрационных сопротивлений являются функцией трех параметров (rс, h, f0) (6) Как _ видим, дополнительное слагаемое R(rc , h, ...
... , и ее численное значение при любом вскрытии пласта всегда меньше численного значения С1(rc, h) при установившемся притоке. 3. Полученное аналитическое решение для неустановившегося притока сжимаемой жидкости (газа) к несовершенной скважине в бесконечном по протяженности пласте преобразовано в прямолинейную анаморфозу, которая позволяет эффективно интерпретировать кривые восстановления забойного ...
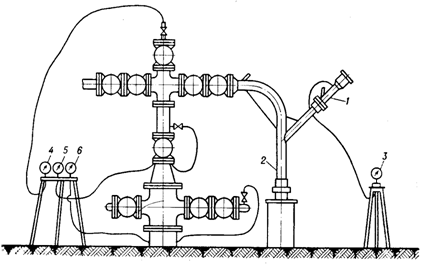
... , интересных с точки зрения нефтенасыщенности, в разрезе скважины нет. В связи с тем, что расстояние до нефтесборной сети более 5км., скважина подлежит консервации. Пример проведения гидродинамических исследований Скважина № 1478 Приразломного месторождение Интервал испытания: 2716-2753,6 м Дата испытания: 17 ноября 1995 г Пласт БС16-18 Условия испытания: Испытание проведено в обсаженном ...
... в 22 скважинах, нижняя – в 44 скважинах. Остальные эксплуатируют верхнюю и нижнюю части одновременно. В настоящее время на Ямсовейском газоконденсатном месторождении находятся в эксплуатации четыре газоконденсатных скважины, пробуренные на ачимовские отложения. Были проведены исследования физико-химических свойств газового конденсата и дана его оценка как углеводородного сырья для производства ...

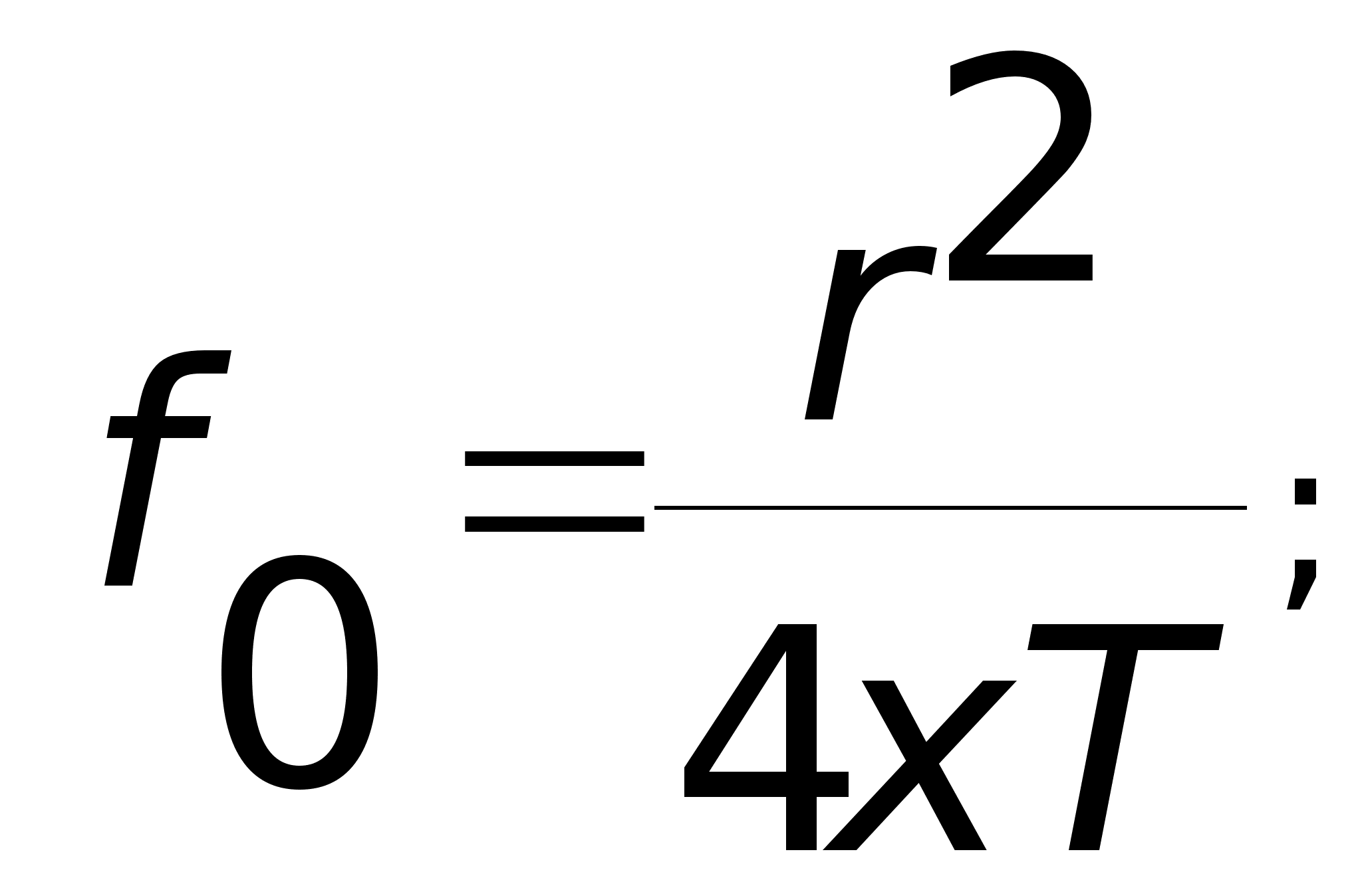
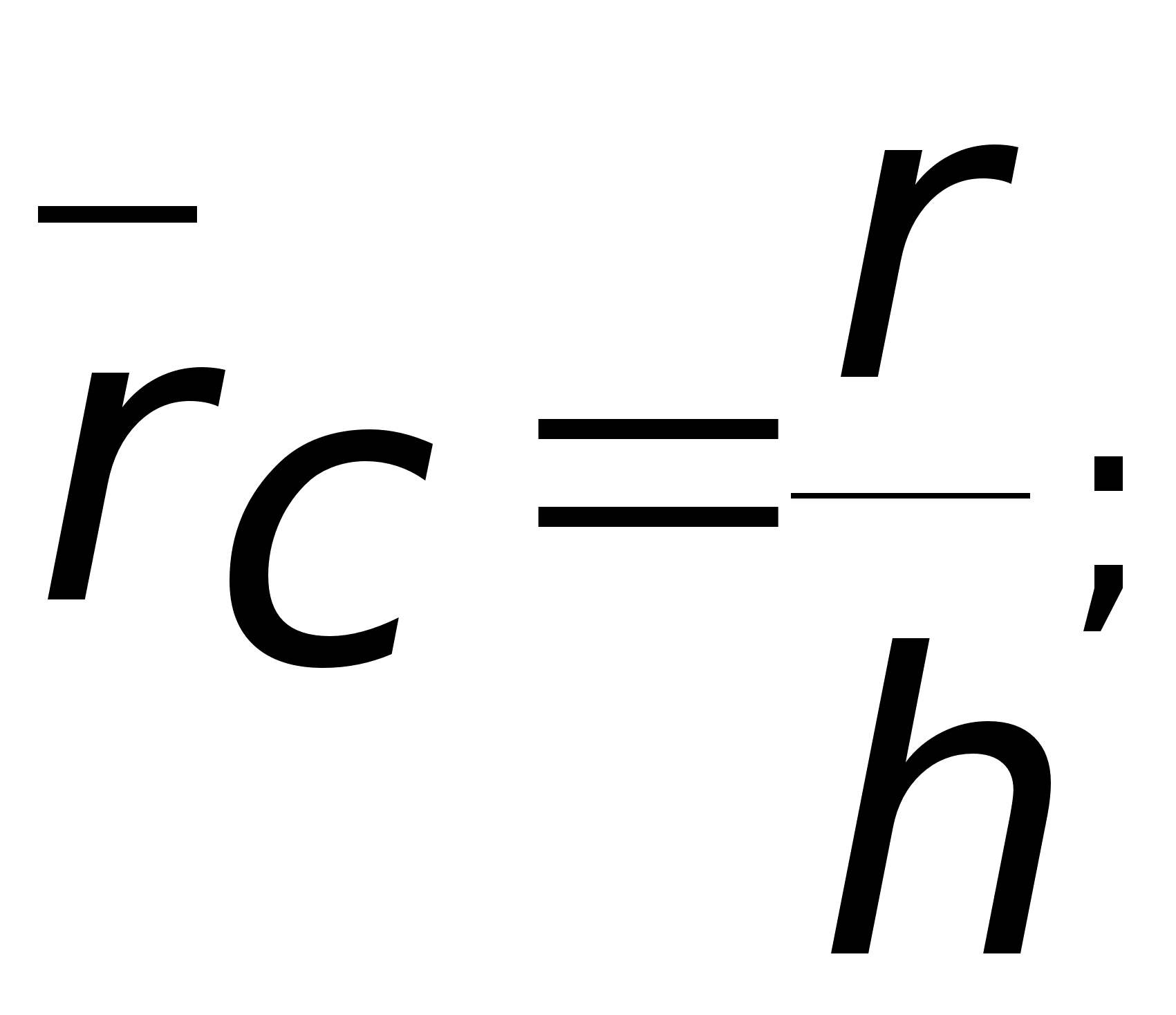
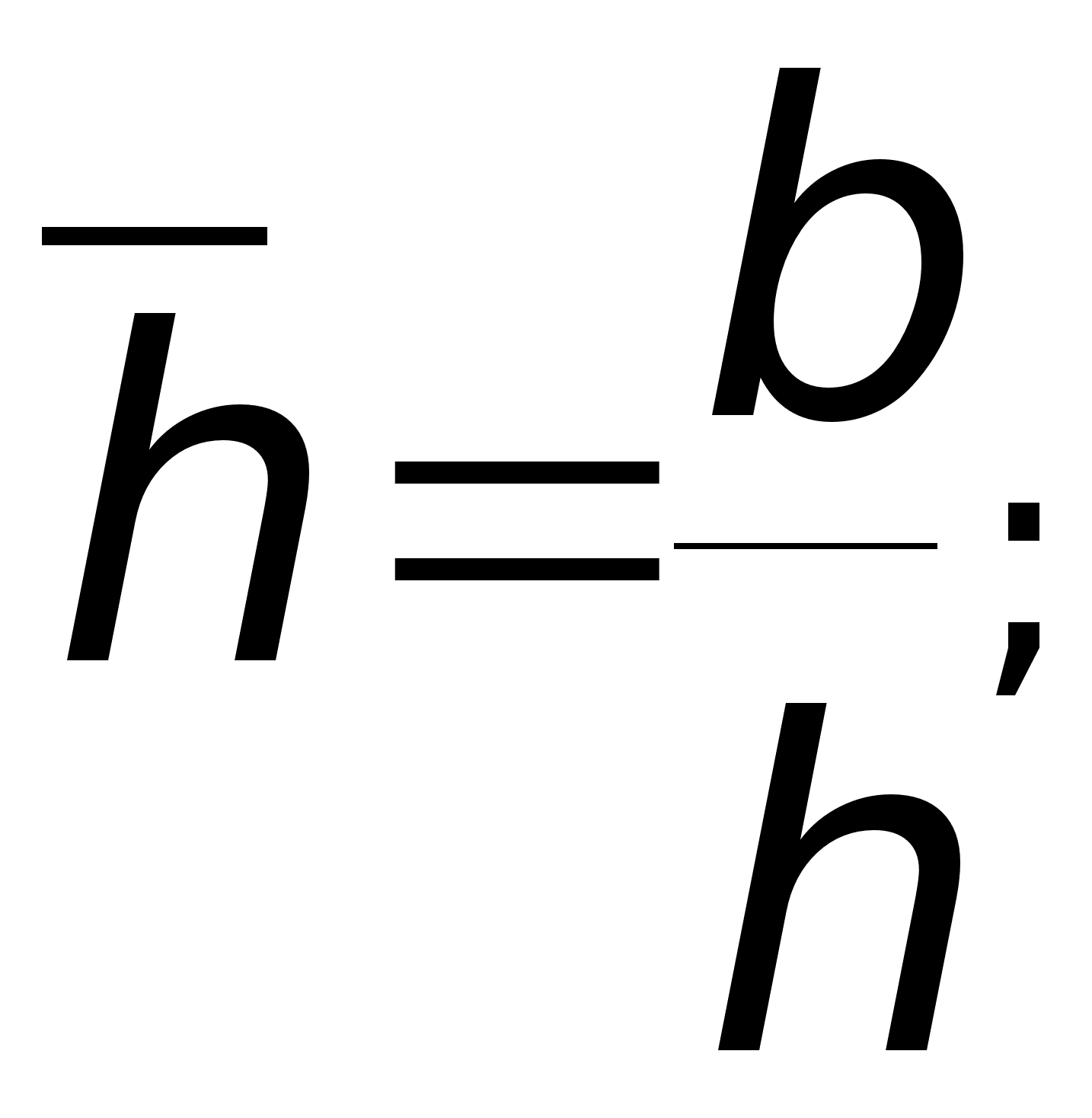
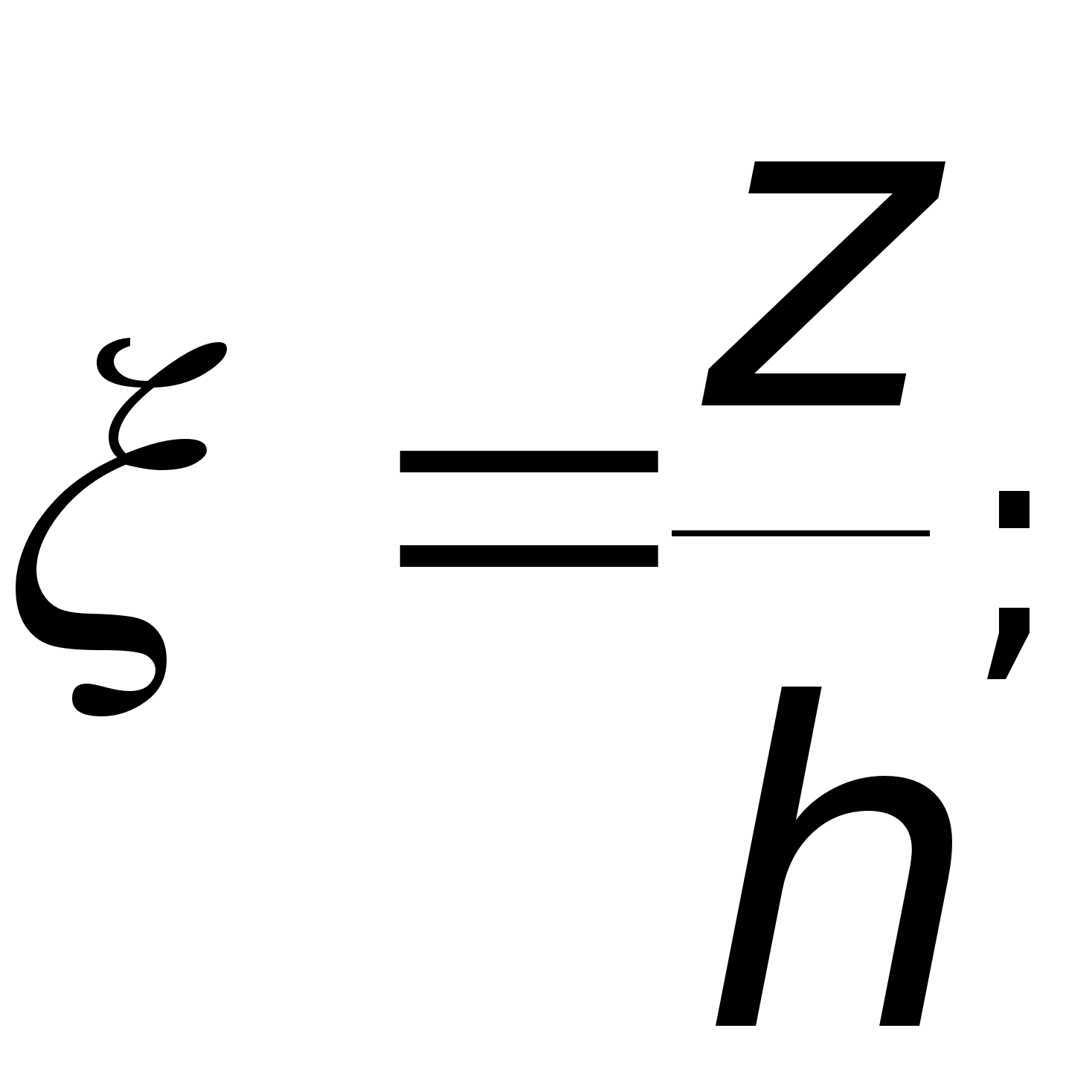
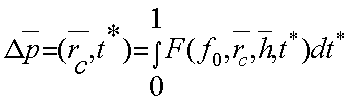
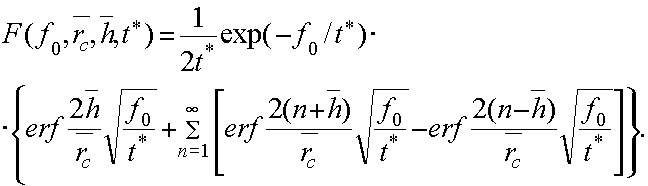
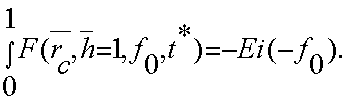
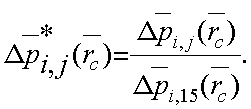

0 комментариев