Навигация
Кинематический анализ механизма
1.2. Кинематический анализ механизма.
1.2.1. Определение скоростей точек и звеньев механизма.
Планом скоростей называется диаграмма, на которой изображены векторы скоростей точек плоского механизма.
Для определения скоростей точек и звеньев механизма воспользуемся методом планов скоростей. Построение планов скоростей начинаем с скорости точки B ведущего звена АB. Учитывая, что скорость ведущего звена w известна, скорость точки B определим из уравнения
V=w×LAB
где LAB – длина звена АB, м.
VB= 40,82*0,03м. = 1,22 м/с
Вектор VB направлен перпендикулярно звену АB.
От произвольно взятой точки P ( полюса плану скоростей) отложим вектор произвольной длины, что численно равен вектору скорости. VB
Масштабный коэффициент скорости m определим из уравнения
mV=VB/PVB
где VB – скорость точки, м / с;
PVB – длина вектора, мм.
m= 1,22/100= 0,01 м/с.мм.
Для определения скорости точки C воспользуемся условием её принадлежности звену – ВС.Скорость точки С определяется из векторного уравнения:
VC=VB+VCB
В этой векторной сумме неизвестно второе слагаемое. Известно, только ,что линия действия этого вектора перпендикулярна к звену BC. Проводим соответствующую линию на плане скоростей через точку в. Второе ур-ние для скорости точки С составляем с учётом неподвижной опоры-1:
VC=V1+VC1
Скорость V1 равна нулю. Скорость VC1 направлена вдоль направления движения ползуна. На плане этой скорости соответствует линия ,параллельная направляющей. На пересечении этой линии и линии перпендикулярной звену BC находится точка с. Численно скорость VC равняется
VC=PVC×mV
где PVC – длина вектора, мм.
VC = 120* 0,01 = 1,2 м./с.
Для нахождения скорости точки Е воспользуемся тем ,что она принадлежит звену ВС и делит звено на равные отрезки. Для векторов скоростей справедливо :
LBC/LEC=bc/ec ,
где LEC-длина звена EC,
ec-длина вектора на плане скоростей.
На плане скоростей точка е находится на отрезке вс деля его в соотношении LBC/LEC. Вектор ,соединяющий полюс с точкой е,соответствует скорости VE ,численное значение которой равно
VE=PvE×mV=97,5*0,01=0,97 м./с.
Определим скорость точки D. Точка D принадлежит звену DE.
Это даёт векторное ур-ние
VD=VE+VDE
В этой векторной сумме неизвестно второе слагаемое.Известно только ,что линия действия этого вектора перпендикулярна звену ED. Проводим соответствующую линию на плане скоростей через точку е. Второе ур-ние составляем относительно неподвижнойопоры:
VD=V1+VD1
V1=0.
VD1-направлена вдоль движения ползуна. На плане этой скорости соответствует линия ,параллельная направляющей. На пересечении это линии и линии перпендикулярной звену DE находится точка d. Численно скорость VD равна :
VD = PVD×mV=79*0,01=0,79 м/с
Построеный план скоростей позволяет определять не только скорости всех точек механизма, а так же величину и направление скоростей звеньев.Определяем угловые скорости звена ЕD и ВС.
wCB=VCB/LCB
где wCB – угловая скорость движения звена CB
VCB-скорость движения точки С относительно В
VCB=cb×mV=54*0,01 = 0,54 м./с.
wCB=0,54/0,09=6 рад/с
Аналогично для звена DE :
wDE=VDE/LDE=mV×de/LDE
wDE=107*0,01/0,115=9,3 рад/с
Направление угловой скорости wCB определяем путём перенесения вектора VCB в точку c на схеме механизма. Направление этого вектора указывает на направление движения звена СВ около точки В. Аналогично и для звена DE.
1.2.2. Определение ускорений точек и звеньев механизма.
Для определения ускорений точек и звеньев механизма воспользуемся методом планов ускорений.
Построение планов ускорений начинаем с ведущего звена механизма. Поскольку wAB = const , то :
aB=w2×LAB=40,822*0,03=49,98 м/с2
Ускорение точки B направлено вдоль звена АB к центру её вращения. С любой произвольной точки PA отложим вектор произвольной длины, что численно равен вектору ускорения точки B.Масштабный коэффициент ускорений найдём таким образом:
![]() mA=aB/PAB=49,98/99=0,5 м/мм×с2
mA=aB/PAB=49,98/99=0,5 м/мм×с2
где PAB – длина вектора, мм.
Для определения ускорения точки C запишем ур-ние плоско-параллельного движения звена ВС :
aE=aB+anCB+atCB
где anCB – центростремительная составляющая ускорения относительно движения точки С около точки В;
atCB – касательная составляющая ускорения точки С относительно точки В.
anCB=V2CB/LCB=(mV×cb)2/ LCB=(0,01*54)2/0,09=3,24 м/с2
Длина соответствующего вектора на плане :
nCB=anCB/mA=3,24/0,5=6,48 мм
На плане ускорений из точки b` проводим вектор nCB , параллельный звену BC и направленный от С к В , а из конца этого вектора - перпендикуляр в обе стороны , который соответствует направлению касательного ускорения atCB.Для исследования движения ползуна необходимо использовать точку 1 на неподвижной направляющей. Тогда ур-ние движения точки С :
aC=a1+aC1
На плане ускорений точка 1 находится в полюсе т.к. она неподвижная
Про aC1 известно , что оно параллельно направляющей. Поэтому на плане через полюс проводится горизонтальная линия.На пересечении этой линии и линии перпендикулярной звену ВС находится точка с`.
Численное значение ускорения :
aC=mA×Pac`
где Pac`- длина вектора , соединяющего полюс с точкой с`.
aC=32*0,5=16 м/с2
Точку е` можно найти на отрезке b`c` соответственно с соотношением :
b`e`/b`c`=LBE/LBC
из которого b`e`=b`c`×LBE/LBC=86,5/2=43,2 мм
Значение ускорения aE определяется по формуле :
aE=mA×PAe=0,5*59=29,5 м/с2
Для нахождения ускорения точки D запишем :
aD=aE+anDE+atDE
Центростремительное ускорение anDE найдём таким образом :
anDE=V2DE/LDE=(mV×de)2/LDE=(107*0,01)2/0,115=9,9 м/с2
Длина соответствующего вектора на плане ускорений :
nDE=anDE/mA=9,9/0,5=19,8 мм
На плане ускорений из точки е` проводим вектор nDE ,параллельный звену DE и направленный от D к E , а из конца этого вектора перпендикуляр в обе стороны , который соответствует направлению касательного ускорения atDE .
Ур-ние движения точки D :
aD=a1+aD1
Т.к. точка 1-неподвижна ,то на плане скоростей точка находится в полюсе. Ускорение aD1 направлено параллельно направляющей , поэтому на плане проводится вертикальная линия . На пересечении её илинии перпендикулярной звену DE НАХОДИТСЯ ТОЧКА d`.Численно ускорение d` равно :
aD=mA×PAd`=41*0,5=20,5 м/с2
Ускорения середины звеньев равны :
aS1=49,9*0,5=24,75 м/с2
aS2=29,5 м/с2
aS4=23 м/с2
Угловое ускорение звена BC определяем из соотношения :
e=atCB/LCB=mA×tBC/LCB
где tBC -длина вектора atCB на плане ускорений
eCB=86,5*0,5/0,09=480 1/с2
Если вектор tBC условно перенести в точку С ,можно найти направление eCB,они направлены в одну сторону.
Для звена DE имеем :
eDE= atDE/LDE=mA×tDE/LDE=36*0,5/0,115=156 1/c2
Его направление находим условным переносомвектора tDE в точку D.
Похожие работы
... длину вектора и переведем ее обратно: = 79 мм = 2370 Н 2. ПРОЕКТНЫЙ РАСЧЕТ ЗВЕНЬЕВ МЕХАНИЗМА НА ПРОЧНОСТЬ 2.1 Выбор расчетной схемы В результате динамического анализа плоского рычажного механизма были определены внешние силы, которые действуют на каждое звено и кинематическую пару. Такими внешними силами являются силы инерции , моменты инерции и реакции в кинематических парах R. Под ...
... Найденные при силовом анализе механизма величины представлены в таблице 1.4. 57 48 65 0.22 0.6 0.8 0.79 0.7 0.9 73 1.9 Таблица 1.4. Силовой анализ механизма 2. ПРОЕКТНЫЙ РАСЧЕТ МЕХАНИЗМА НА ПРОЧНОСТЬ В результате динамического анализа плоского рычажного механизма были определены внешние силы, действующие на каждое ...
... 74 R05 24.4 0,005 G4 14,7 Fi4 7.02 R04 7.6 G5 24,5 Fi5 8.125 Fур 0,197 2 ПРОЕКТНЫЙ РАСЧЕТ МЕХАНИЗМА НА ПРОЧНОСТЬ В результате динамического анализа плоского рычажного механизма были определены внешние силы, действующие на каждое звено и кинематическую пару. Этими ...
... напряжений; 4) определить размеры детали и округлить их до ближайших стандартных, согласно которым будет производится подбор сечений. 2.1 Выбор расчетной схемы В результате динамического анализа плоского рычажного механизма были определены внешние силы, которые действуют на каждое звено и кинематическую пару. Проектный расчет на прочность будем производить для группы Ассура 2-4 данного ...
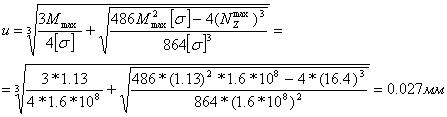
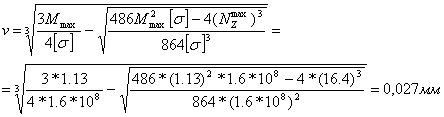

0 комментариев