Навигация
Силовой анализ механизма
1.3 Силовой анализ механизма
Метод силового анализа механизма с использованием сил инерции и установления динамического уравнения носит название кинестатического расчета. Этот расчет основан на принципе д'Аламбера, который предполагает, что в общем случае все силы инерции звена, совершающие сложное движение, могут быть сведены к главной векторной силе инерции ![]() и к паре сил инерции
и к паре сил инерции ![]() , которая определяется по формулам
, которая определяется по формулам
![]() ;
;
![]() ,
,
где m – масса звена;
![]() – ускорение центра масс;
– ускорение центра масс;
![]() – момент инерции звена относительно оси проходящей через центр масс звена;
– момент инерции звена относительно оси проходящей через центр масс звена;
E – угловое ускорение звена.
Сила инерции звена направлена противоположно ускорению, а момент инерции ![]() в сторону обратную направлению углового ускорения.
в сторону обратную направлению углового ускорения.
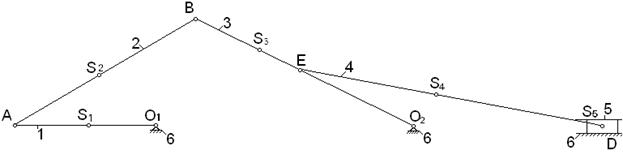
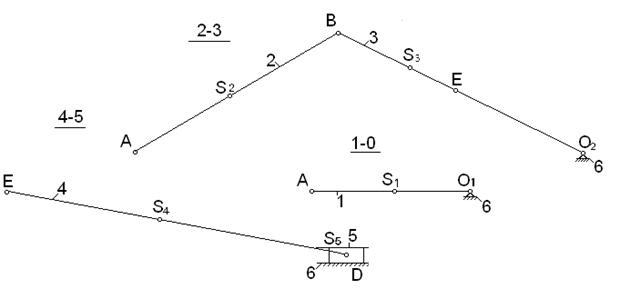
Делим механизм на группы Ассура.
Нам дано: g = 2,4 кг/м; а масса звена равна m = gl, тогда:
mAB= 0,03*2,4 =0,072 кг. P1=0,072*9,8=0,705 H
mBC= 0,09*2,4 = 0,216 кг. P2=0,216*9,8=2,116 H
mDE= 0,115*2,4 = 0,276 кг. P3=1,8*9,8=17,64 H
P4=0,276*9,8=2,704 H
P5=1,2*9,8=11,76 H
Момент инерции стержня определяется по формуле
![]() ;
;
IBC=0,216*0,092/12=0,00014 кг×м2
IED=0,276*0,1152/12=0,0003 кг×м2
Сила инерции определяется:
![]()
Fu1=0,072*24,75=1,78 H
Fu2=29,5*0,216=6,37 H
Fu4=23*0,276=6,348 H
Момент инерции определяем как
![]()
Mu2=IBC×eBC=0,00014*480=0,067 H
Mu4=IED×eED=0,0003*156=0,046 H
Для нахождения реакций в кинематических парах разбиваем механизм на группы Ассура. Начнем с группы звеньев наиболеее удаленной от ведущего звена.Это группа 4-5.Шарнирные связи заменяем реакциями RE и R5. Ракция в шарнире Е неизвестна ни по модулю ни по направлению, поэтому раскладываем её на составляющие :REn-по направлению оси и REt-перпендикулярно ей. Реакция в шарнире D неизвестна по модулю и направлена перпендикулярно оси OY.
åMD=M4+Fi4×hi4-P4×H4-REt×LDE=0
Отсюда :
REt= M4+Fi4×hi4-P4×H4/LDE=0,046+6,348*0,047-2,704*0,029/0,115=2,313 Н
Для определения REn и R5 рассмотрим ур-ние равновесия 2-х поводковой группы :
REn+REt+Fi4+Fi5+R5+P4+P5+Pпс=0
Согласно с этим векторным ур-нием строится замкнутый силовой многоугольник. На чертеже выбирается полюс и от него проводим вектор произвольной длины согласно направлению одной из сил. Масштабный коэффицент вычисляется по формуле :
mF=Fi5/PFFi5=24,6/120=0,2
где PFFi5-длина соответствующего вектора на плане сил.
После этого к вектору Fi5 в произвольном порядке достраиваем остальные слагаемые векторного ур-ния, пересчитывая длины векторов через масштабный коэффицент. Используя план сил определим модули сил RE и R5.
RE=122*0,2=24,4 H
R5=53*0,2=10,6
Для определения реакций в шарнирах B и C рассмотрим группу 2-3.
Шарнирные связи заменяются реакциями RB и R3. Реакция в шарнире Е известна из рассматриваемойй ранее кинематической пары и берется с противоположным направлением. Реакция в шарнире В неизвестна, поэтому раскладываем её на составляющие RBt и RBn.
Реакция в шарнире С направлена перпендикулярно оси OX.
Сумма моментов относительно С равна нулю , отсюда
RBt=(RE×hR+Fi2-M2-P2×H2)/LBC=6,015 H
Для определения RBn и R3 рассмотрим ур-ние :
RBt+RBn+RE+Fi2+Fi3+R3+P2+P1=0
Согласно с этим векторным ур-нием строится замкнутый силовой многоугольник. На чертеже выбирается полюс и от него проводим вектор произвольной длины согласно направлению одной из сил. Масштабный коэффицент вычисляется по формуле :
mF= Fi3/PF Fi3=28,8/144=0,2 Н/мм
Используя план сил определим модули сил RBи R3:
RB=121*0,2=24,2 H
R3=59*0,2=11,8 H
Ведущее звено.
Запишем ур-ние моментов относительно точки В :
åM=-RAt×LAB+P1×H1=0 RAt=P1×H1/LAB=0,19 H
Для определения RAn и Pур запишем векторное ур-ние равновесия сил
RAn+ RAt+ RB+ Fi1+ P1+ Pур=0
Согласно с этим векторным ур-нием строится замкнутый силовой многоугольник. Масштабный коэффицент вычисляется по формуле :
mF= RB/ PF RB=46,4/90=0,5 Н/мм
Используя план сил определим модули сил RAи Pур:
RA=28*0,5=14 H
Pур=42*0,5=21 H
Результаты измерений сведены в таблицах
| точка \ пар-тр | B | C | E | D | S1 | S2 | S4 | CB | DE |
| V,м/с | 1,22 | 1,2 | 0,97 | 0,79 | 0,61 | 0,71 | 0,99 | ||
| a,м/с2 | 49,98 | 16 | 29,5 | 20,5 | 24,75 | 29,5 | 23 | ||
| e,1/С2 | 480 | 156 |
| ЗВЕНЬЯ \ ПАРАМЕТР | 1 | 2 | 3 | 4 | 5 |
| m, кг | 0,072 | 0,216 | 1,8 | 0,276 | 1,2 |
| I, кг×м2 | 0,00014 | 0,0003 | |||
| Fu, Н | 1,78 | 6,37 | 6,348 | ||
| Mu, Н×м | 0,067 | 0,046 |
| точки \ реакции | A | B | C | D | E |
| Rt, H | 0,19 | 6,015 | 2,313 | ||
| Rn, H | 14 | 23,4 | 22 | ||
| R, H | 14 | 24,2 | 11,8 | 1 | 22,2 |
2. Расчет элементов кинематических пар на прочность.
2.1. Определение внешних сил, действующих на звенья.
В результате динамического
анализа плоского рычажного механизма определены внешние силы, действующие на звенья и кинематические пары. Такими внешними усилиями являются силы инерции F ![]() , моменты инерции M
, моменты инерции M![]() , а также реакции кинематических пар R, силы веса и полезного сопротивления.
, а также реакции кинематических пар R, силы веса и полезного сопротивления.
Под действием внешних сил звенья плоского механизма испытывают сложные деформации. Для заданного механизма преобладающим видом совместных деформаций является изгиб с растяжением – сжатием. Рассмотрим группу 4-5 как груз на двух опорах , нагруженных соответствующими силами, т.е. выбираем расчетную схему.
2.2. Расчетная схема.
Из ур-ния суммы моментов относительно точки Е найдем опорную реакцию КД :
åME=M4+(P4t-Fi4t)×LDE/2 + (-Pпсt-Fi5t+R5t+P5t)×LDE-KD×LDE=0
Отсюда найдем KD:
KD=(0,046+(2,704-5,383)0,057+(-2,5-12,3+10,392+5,88)0,115)/0,115=
= -0,083 H
Из ур-ния суммы моментов относительно D найдем опорную реакцию КE :
åMD=(KE×REt)LDE-M4+(P4t-Fi4t)LDE/2
Отсюда найдем КE :
КE =(-0,115*2,313+0,046+(5,383-1,473)*0,0575)/0,115=0,043 H
Из ур-ния åNZ=0 найдём опорную реакцию НЕ:
HE=REn+P1n-Fi4n+P5n-Fi5n-Pпсn-R5n=
=22+2,268-3,364+10,184-21,304-4,33-6= -0,546
2.3. Построение эпюры NZ.
Используя метод сечений для нормальной суммы NZполучаем такие ур-ния :
NZ1=R5n+Pпсn+Fi5n-P5n=6+4,33+21,304-10,18=21,454 H
NZ2=HE+Ren=22,546 H
По этим ур-ниям строим эпюру NZ
2.4. Построение эпюры Qy.
Для поперечной силы Qy ,используя метод сечений записываются такие аналитические ур-ния :
Qy1=-KD+Fi5t+Pпсt-P5t-R5t=-0,083+12,3+2,5-5,88-10,392=-1,56 H
Qy2=REt-KE=2,313-0,043=2,27 H
По этим ур-ниям строим эпюру Qy.
2.5. Построение эпюры Mx.
На участках 1 и 2 записываем ур-ния для изгибающего момента :
Mx1=(Fi5t+Pпс-P5t-R5t-KD)×z1 0£Z1£0,0575
Mx1={0;-0,089}
Mx2=-(REt+KE)Z2 0£Z2£0,0575
Mx2={0;-0,135}
По этим ур-ниям строим эпюру Mx, из неё видно ,что опасное сечение проходит через точку S4 , потомучто в ней изгибающий момент Mx и нормальная сила-максимальны :
Mmax=0,135 Н×м Nmax=22,5 H
2.6.Подбор сечения.
Из условия smax=Mxmax/Wx£[s] находим
Wx=0,135*1000/1200=0,1125 см
Находим по сортаменту размер двутавра
1) Круглое сечение Wx=p×d3»0,1d3
d=1,125 см
2) Прямоугольное сечение Wx=bh2/6=4b3/6
b=0,41 см
h=0,82 см
Материал звеньев СТ 3 [s]=120 МПа
![]() ВЫВОДЫ.
ВЫВОДЫ.
Цель курсового проектирования – закрепление теоретических знаний, что были получены во время изучения курса “Техническая механика”, ознакомление с методами проектирования механизмов. Первый этап конструирования любого механизма – это составление его кинематической схемы, расчет кинематических параметров, определение нагрузки различных деталей и энергетических характеристик механизма в целом.
Выполняя курсовой проект по технической механике, овладел методами определения кинематических параметров механизмов, оценки сил, что действуют на отдельные звенья механизма, научился творчески оценивать сконструированный механизм с точки зрения его назначения – обеспечивать необходимые параметры движения звена.
Похожие работы
... длину вектора и переведем ее обратно: = 79 мм = 2370 Н 2. ПРОЕКТНЫЙ РАСЧЕТ ЗВЕНЬЕВ МЕХАНИЗМА НА ПРОЧНОСТЬ 2.1 Выбор расчетной схемы В результате динамического анализа плоского рычажного механизма были определены внешние силы, которые действуют на каждое звено и кинематическую пару. Такими внешними силами являются силы инерции , моменты инерции и реакции в кинематических парах R. Под ...
... Найденные при силовом анализе механизма величины представлены в таблице 1.4. 57 48 65 0.22 0.6 0.8 0.79 0.7 0.9 73 1.9 Таблица 1.4. Силовой анализ механизма 2. ПРОЕКТНЫЙ РАСЧЕТ МЕХАНИЗМА НА ПРОЧНОСТЬ В результате динамического анализа плоского рычажного механизма были определены внешние силы, действующие на каждое ...
... 74 R05 24.4 0,005 G4 14,7 Fi4 7.02 R04 7.6 G5 24,5 Fi5 8.125 Fур 0,197 2 ПРОЕКТНЫЙ РАСЧЕТ МЕХАНИЗМА НА ПРОЧНОСТЬ В результате динамического анализа плоского рычажного механизма были определены внешние силы, действующие на каждое звено и кинематическую пару. Этими ...
... напряжений; 4) определить размеры детали и округлить их до ближайших стандартных, согласно которым будет производится подбор сечений. 2.1 Выбор расчетной схемы В результате динамического анализа плоского рычажного механизма были определены внешние силы, которые действуют на каждое звено и кинематическую пару. Проектный расчет на прочность будем производить для группы Ассура 2-4 данного ...
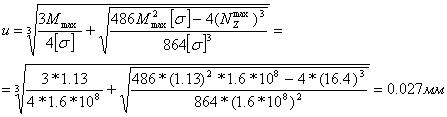
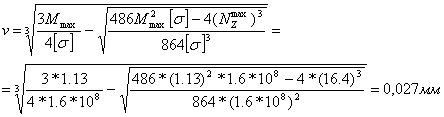
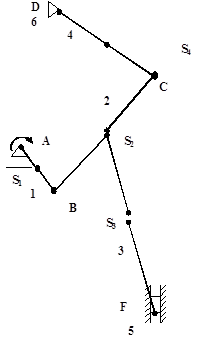

0 комментариев