Навигация
Обоснование проектных решений
3.3.2. Обоснование проектных решений
3.3.2.1. Анализ при постоянной интенсивности наращения
Модель непрерывного начисления процентов
В банковской практике — особенно при электронных методах производства и регистрации финансовых операций - проценты могут начисляться за 1 сутки или даже за несколько часов. Например, коммерческий банк, находящийся в Москве, может одолжить определенную сумму денег банку, находящемуся во Владивостоке, на 12 часов — с 20 часов сегодняшнего дня до 8 часов следующего дня по московскому времени. За счет разницы во времени Владивостокский банк может добавить эти деньги к своему фонду краткосрочных ссуд, а затем вернуть долг с определенным процентом (или долями процента) к началу работы московского банка. Очевидно, что в этом и другом аналогичных случаях возникает задача начисления процентов за очень малые промежутки времени, т.е. по существу речь идет о непрерывном начислении процентов и их непрерывной капитализации.
При анализе инвестиций также возникает аналогичная задача, поскольку многие производственные и экономические процессы непрерывны по своей природе и такой же должна быть соответствующая им финансовая модель. В главах 1 и 2 мы построили несколько моделей начисления процентов при различной длине периода начисления (конверсионного периода) — от 1 дня до 1 года. Устремляя длину периода начисления к 0, построим теперь математическую модель непрерывного начисления процентов, рассмотрим способы практического применения непрерывной модели, а также сравним результаты дискретного и непрерывного начисления процентов. Для краткости иногда говорят "непрерывные проценты" , имея в виду непрерывное начисление и капитализацию процентов, т.е. бесконечно малый период начисления.
Постоянная интенсивность наращения
Примем за базовый период 1 год и обозначим целое число периодов начисления за год через т, а длину периода начисления через h = 1/т лет, m = 1,2,3,... . Тогда соответствующая положительная годовая ставка, и в силу формулы она связана с эффективной годовой ставкой.
Для простоты обозначим i — номинальная процентная ставка за один период начисления длиной h лет. Тогда из при h = m = 1 получаем
Для практики эффективную годовую ставку удобнее обозначать просто i.
Сделаем небольшое математическое пояснение. Для этого запишем коэффициент А(h) наращения эа любой период
(t, t + h) длиной h = 1/m на рассматриваемом интервале (О, T) в виде
Поскольку h мало, то различие между простыми и сложными процентами пренебрежимо мало. Так как A(0)=1, то— приращение 1 ден. ед. за малое время h (рис. 9.1, где h и т измеряются в годах).
Если А(т) дифференцируема в точке 0 справа, то
где g — угол наклона касательной к А(т) в точке т = 0.Из определения рассматриваемых ставок и результатов п. 2 § 8 следует, что если эффективная ставка i фиксирована, то номинальная ставка, при т —> и h = 1/т —> О монотонно убывает, оставаясь положительной. Поэтому существует положительное предельное значение, которое мы обозначим через: W.
ОПРЕДЕЛЕНИЕ. Предел 6 номинальной ставки W при т —> называется силой роста или интенсивностью наращения за год при непрерывном начислении процентов. Величину 8 можно назвать также номинальной годовой ставкой при непрерывном начислении процентов.
ТЕОРЕМА 3.1. Эффективная годовая ставка i и номинальная годовая ставка связаны соотношением
Доказательство. В курсе "Алгебра и начала анализа" доказывается, что
е = 2,718282 ... — замечательное число Эйлера (основание натуральных логарифмов). Поэтому в нашем случае
СЛЕДСТВИЕ.Справедлива и следующая двойственная к теореме 3.1
ТЕОРЕМА 9.2. Эффективная годовая ставка d дисконтирования и номинальная годовая ставка связаны соотношением
Для доказательства достаточно перейти к пределу в (3.7) при, использовав при этом вышеприведенные формулы.Формула (3.6) и соотношение и (3.2) позволяют составить таблицу 3.21, иллюстрирующую связь для нескольких значений i от 0,01 до 2) и при малых 1 до 0,10 достаточно близки. Однако с ростом 1" различие между тремя эквивалентными ставками быстро растет.
Таблица 3.21.
| D | G | I |
| 0,00990 | 0,00995 | 0,01 |
| 0,04761 | 0,04879 | 0,05 |
| 0,09091 | 0,09531 | 0,10 |
| 0,16667 | 0,18232 | 0,20 |
| 0,20000 | 0,22314 | 0,25 |
| 0,33333 | 0,40547 | 0,50 |
| 0,42857 | 0,55962 | 0,75 |
| 0,50000 | 0,69315 | 1,00 |
Пример 3.1. Найдем наращенное за 5 лет значение суммы S(0)=10 руб., если оно реинвестируется по постоянной ставке = 25% при следующих значениях m:
а) 1 раз в год,
б) 2 раза в год,в) непрерывно.г) Вычислим g для непрерывного начисления процентов.
Пример 3.2. Найдем коэффициент наращения A(т) за т = 1 год при реинвестировании по постоянной ставке = 1 ежегодно, ежеквартально, ежемесячно, ежечасно ежеминутно и непрерывно. Вычислим для каждого из случаев.
Таблица 3.22.
| Период начисления | m | A(1)=(1+1/m)m | iэф = A(1)-1 |
| Ежегодное Ежеквартальное Ежемесячное Ежедневное Ежечасное Ежеминутное Непрерывное | 1 4 12 360 8640 518400 | (1+1/1)1 =2 (1+1/4)4 =2,441406 (1+1/12)12 =2,613035 (1+1/360)360 =2,714516 (1+1/8640)8640 =2,718125 (1+1/518400)51840=2,718276 e=2,718282 | 1 1,441406 1,613035 1,714516 1,718125 1,718276 1,718282 |
Функциональная связь между любыми парами из основных параметров
В зависимости от условий задачи может оказаться удобным принять один из четырех основных параметров i, v и d за исходный и выразить через него значения трех остальных. В табл. 3.3 объединены ранее полученные соотношения.
Каждая строка этой таблицы показывает, как параметр, стоящий в обозначении этой строки, выражается через три остальные. Каждый столбец таблицы показывает, как через параметр, стоящий в обозначении этого столбца, выражаются три остальные.
Приближенная связь между основными параметрами
Из теории рядов известно, что при малых х с точностью до членов третьего порядка малости включительно
Подставляя первую из этих формул в (3.4), а вторую — в (3.6) и пренебрегая членами третьего порядка, получим, что при i или не более 0,10-0,20 можно пользоваться приближенными соотношениями: Аналогичным образом из формулы для суммы бесконечного числа членов сходящейся прогрессии следует, что при малых i
Этими приближенными формулами можно пользоваться для ориентировочных расчетов. Однако в финансовой практике надо пользоваться калькулятором или таблицами даже при малых i и
Коэффициенты наращения и дисконтирования при непрерывном наращении процентов
Предположим, что в настоящий момент tо производится инвестиция в сумме S(tо) по постоянной эффективной годовой ставке i. Тогда в силу формулы (3.5) для сложных процентов наращенная к моменту t = tо + т сумма АV1 составит
где время измеряется в годах, а i и g = ln(1+i) — десятичные дроби.
Если же нам предстоит в будущий момент t > tо уплатить или получить сумму S(t), то ее современная приведенная стоимость РV в настоящий момент tо составит
Итак, нами доказана следующая важная
ТЕОРЕМА 3.3. При постоянной эффективной годовой ставке i к номинальной годовой ставке ln(1 + i) коэффициент наращения зависит лишь от длины т интервала наращения, измеренной в годах, и составляет
Коэффициент дисконтирования за т лет равен
Заметим теперь, что А(т) — коэффициент наращения 1 ден. ед. на интервале (tо, tо + т} при движении по этому интервалу слева направо, т.е. в положительном направлении.
Равенство можно интерпретировать как отрицательное наращение, совпадающее с дисконтированием, поскольку движение по интервалу (t, t + т) происходит справа налево, т.е. в отрицательном направлении. Аналогичным образом интерпретируется равенство
Следовательно, в рассматриваемом случае коэффициенты наращения и дисконтирования взаимозаменяемы и с математической точки зрения можно было бы пользоваться только одним из них. Однако для наглядности удобнее пользоваться двумя коэффициентами в соответствии с прямым содержательным смыслом каждого из них.
Таким образом, как при дискретном, так и при непрерывном начислении сложных процентов справедливо фундаментальное соотношение
В частности, при т = 1 получаем из ранее установленных соотношений
Заметим теперь, что если функцию е задать на интервале то [-;+] при т > 0 она совпадает с А(т), а при т < 0 — с v(т):
При этом А'{0) — интенсивность наращения за базовую единицу времени.
Пример 3.3. Сумма 2000 долл. положена в банк под схему непрерывного начисления процентов с постоянной интенсивностью роста 10% за год. Найдем наращенную в конце года t сумму S(t) при t= 1, 2, 3, 5 и 10.
Решение. Здесь S(t) = 2000е, и ответ содержится в таблице 3.23.
Таблица 3.23.
| t, лет | 0 | 1 | 2 | 3 | 5 | 10 |
| S(t), $ | 2000 | 2210,34 | 2442,81 | 2699,72 | 3297,44 | 5436,56 |
Пример 3.5. Заемщик В должен уплатить кредитору А по векселю1000 долл. на 01.01.96, 2500 долл. на 01.01.97, 3000 долл. на 01.07.97.Найдем современную стоимость долга С(t) на моменты:а) 01.01.94 и б) 01.04.95 при = 0,06 за год.
Похожие работы
... операций в несколько раз. 4 Обоснование экономической эффективности проекта Задачей проекта является проектирование автоматизированной системы управления документооборотом Отдела организации деятельности участковых уполномоченных милиции Ленинского РОВД. Результатом проекта является снижение трудоемкости, сокращение объема документооборота, повышение достоверности и качества входящей и ...
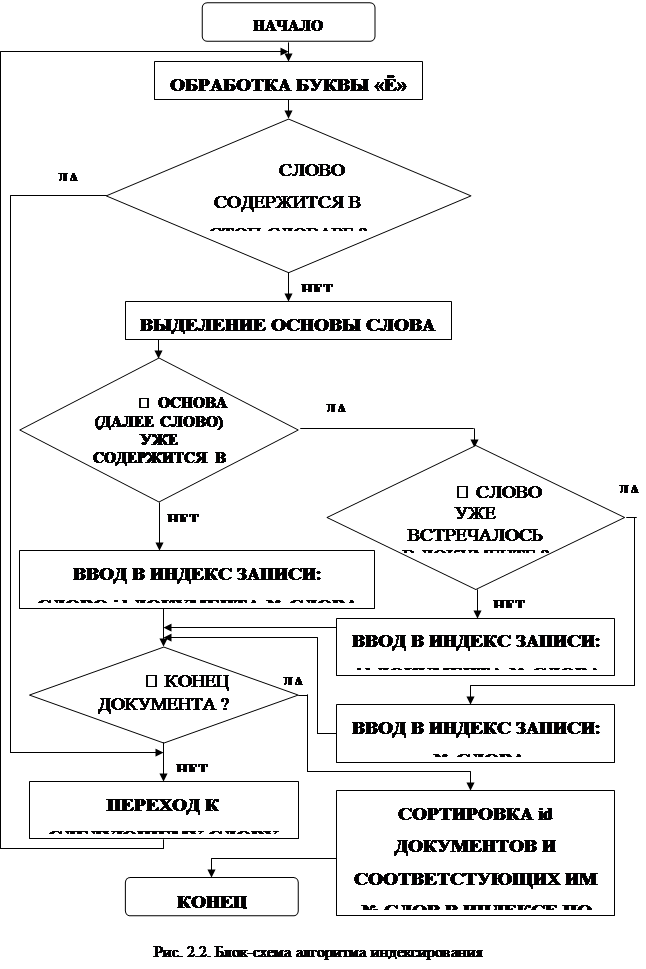
... , практически, не используются. Проблема информатизации Минторга может быть решена путем создания Автоматизированной Информационной системы Министерства Торговли РФ (АИС МТ РФ) в соответствии с настоящим Техническим предложением. ГЛАВА 2. МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ КОМПЛЕКСА ЗАДАЧ "СИСТЕМА ДОКУМЕНТООБОРОТА УЧЕРЕЖДЕНИЯ”. функции поиска и архивации 2.1. Постановка задачи и её спецификация ...
... · (25 – 20)· 80 / 1992=11752,41рублей, что составляет 20% от годового фонда заработной платы менеджера 11 разряда, занятого подготовкой и переработкой документов в автоматизированной системе документооборота. 5.2. Экономия затрат на оплату машинного времени При замене базового программного продукта (ПП) на новое, как правило, уменьшается время использования вычислительных средств. Расчет ...
... сетям, что позволяет иметь более полную информацию о рынке труда в целом и даже об отдельных работниках - их прошлых мест работы, специализации, квалификации и т.п. 2. Анализ информационно-технического обеспечения системы управления персоналом ООО "БТСП" 2.1 Краткая характеристика предприятия ООО "БТСП" ООО "БТСП" - это предприятие по перевозке пассажиров, грузов и ремонту прочих ...
0 комментариев