Обоснование проектных решений

2.2. Обоснование проектных решений

2.2.1. Математическая модель метода главных компонент

Известно, что истинная величина изучаемого объекта содержит по крайней мере два компонента: истинную характеристику оцениваемого явления и ошибку измерения, которая зависит от большого числа причин. Если измерения проводятся в таких областях, как экономика, биология, медицина, психология, то добавляется третья составляющая, зависящая от вариабельности изучаемого признака, индивида или объекта. Таким образом, зарегистрированное значение может быть представлено в виде суммы , где - зарегистрированное значение изменяемого признака н i-ого объекта исследования, - истинное значение (математическое ожидание) измеряемого признака у i - ого индивида, - вариативное значение изменяемого признака i - ого индивида, - ошибка измерения при определении j - ого признака у i - ого объекта исследования.

В основу метода главных компонент положена линейная модель. Если N - число исследуемых объектов, n - число признаков, то математическая модель принимает вид:

, (2.1)

где r,j =1,2,...n; f - r-я главная компонента; - вес r-ой компоненты в j-ой переменной; -нормированное значение j-ого признака, полученное из эксперимента, на основе наблюдения. В матричной форме y=Af.

Для исследования начальными данными являются ковариации или коэффициенты корреляции. В дальнейшем будем использовать коэффициенты корреляции.

Для установления связи между главными компонентами и коэффициентами корреляции перепишем формулу для любого i в виде:

(2.2)

Вариабельность, зависящая от особенностей объектов, является причиной разброса показаний признаков от объекта к объекту относительно математического ожидания. Полная дисперсия выражается через дисперсию главных компонент, а так как дисперсии нормированных величин равны единице, то можно записать:

.(2.3)

Поскольку главные компоненты ортогональны, то выражение упрощается . Слева записана дисперсия, а справа доли полной дисперсии, относящиеся к соответствующим главным компонентам. Дисперсия является характеристикой изменчивости случайной величины, её отклонений от среднего значения. Полный вклад r-ого факторов дисперсию всех n признаков определяет ту долю общей дисперсии, которую данная главная компонента объясняет.

Этот вклад вычисляется по формуле:

(2.4)

Различают два вида компонент, общие и генеральные. Генеральные главные компоненты существенно связаны со всеми признаками задачи, общие - более чем с одним.

Несмотря на то, что вместо признаков получено такое же количество главных компонент, вклад в общую дисперсию большинства оказывается небольшим. Можно исключить из рассмотрения те компоненты, вклад которых мал.

Итак, при проведении эксперимента мы получаем результаты в виде матрицы наблюдаемых величин ХN,n где N - число наблюдаемых объектов, n - число измеряемых признаков.

Элементы данной матрицы центрируются и нормируются, и мы получаем матрицу Y.

Выясним, что представляют собой весовые коэффициенты между признаками и главными компонентами. Для этого умножим на первую главную компоненту и получим:

. (2.5)

Чтобы получит коэффициент корреляции между j-ым признаком и первой главной компонентой, просуммируем левую часть по всем N наблюдениям и разделим сумму на число наблюдений N, тогда правая часть примет вид:

. (2.6)

Учитывая, что , перепишем выражение:

, (2.7)

где -коэффициент корреляции между j-ым признаком и r-й главной компонентой, - коэффициент корреляции между r-й и первой главной компонентой, - весовые коэффициенты, которые называются в факторном анализе коэффициентами отображения. Поскольку в методе главных компонент компоненты не коррелированны между собой, можно записать =0 (r¹ k), поэтому =. И в общем случае в методе главных компонент можно написать =.

Матрица наблюденных коэффициентов корреляции может быть представлена так:

R=YY¢ , (2.8)

где Y - матрица нормированных значений признаков, Y¢ - транспонированная матрица.

Коэффициент корреляции характеризует связь между двумя случайными величинами Хj и Хr в случае линейной корреляции между ними. Коэффициент корреляции представляет эмпирический первый основной смешанный момент. Для любых признаков и случайных величин , (2.9)

Среднее значение случайной величины Хj определяется по формуле

, (2.10)

а среднеквадратическое отклонение

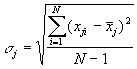. (2.11)

В результате преобразований корреляционной матрицы можно получить y=UL 1/2f, где L -матрица собственных значений матрицы R, U - матрица из собственных векторов R. Отсюда можно заключить, что искомая матрица А может быть определена как А=UL 1/2, или, соответственно для столбцов .

2.2.2. Геометрическая интерпретация метода главных компонент

Геометрической интерпретацией метода главных компонент служит переход к новой системе координат, где осями служат главные компоненты распределения. [3,11].

Рассмотрим простейший двумерный случай. Она представлена на Рис 2.1.

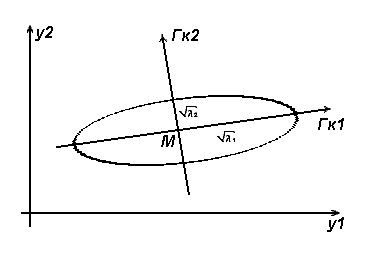
Рис. 2.1. Геометрическая интерпретация метода главных компоент для двумерного случая

Похожие работы

Организация медицинского освидетельствования при проведении военно-врачебной экспертизы в органах внутренних дел

Скачать

33174

1

0

... освидетельствование в органах внутренних дел должно проводиться по единой методике, что позволяет получить наиболее полное представление о состоянии здоровья конкретных освидетельствуемых. Для проведения военно-врачебной экспертизы в органах внутренних дел создаются штатные и нештатные (постоянно и временно действующие) военно-врачебные комиссии и врачебно-летные комиссии. На ВВК в соответствии ...

Из истории организаций, оказывающих экстренную медицинскую помощь, в России и других странах. Их настоящее и перспективы развития.

Скачать

51944

0

7

... , сбором донорской крови), но и по сей день одной из приоритетных областей его деятельности остается оказание экстренной медицинской помощи, всем кто в ней нуждается. «Красный крест» является международной организацией, а это крайне важно, так как поддержка государств друг другом при чрезвычайных ситуациях, часто способствует обеспечению лучшей помощи пострадавшим, а следовательно, и спасению ...

Правовые основы организации военной службы

Скачать

133062

0

0

... лояльности лишенного гражданства лица и его родных к государству бывшего гражданства, а тем более укреплению связей между этим государством и государством военной службы. И если нежелательная иностранная военная служба дает моральную, но не правовую основу утраты гражданства37, особенно при состоянии войны, то при вынужденной службе мы не обнаруживаем и их. Считаем, что нежелательная служба не ...

Военная служба и порядок её прохождения

Скачать

70779

0

0

... военной службы. Под условиями прохождения военной службы следует понимать урегулированные правовыми нормами обстоятельства и факты, образующие в своей совокупности порядок прохождения военной службы. Таким образом, прохождение военной службы – это регулируемый федеральными конституционными законами, федеральными законами, Положением о порядке прохождения военной службы, воинскими уставами и ...