Навигация
ПОИСК В АЛЬТЕРНАТИВНЫХ ПРОСТРАНСТВАХ
3.3. ПОИСК В АЛЬТЕРНАТИВНЫХ ПРОСТРАНСТВАХ
Рассмотренные выше методы поиска исходят из молчаливой предпосылки, что знания о предметной области и данные о решаемой задаче являются точными и полными и для них справедливо следующее:
· все утверждения, описывающие состояние, являются истинными;
· применение оператора к некоторому состоянию формирует некоторое новое состояние, описание которого состоит только из истинных фактов.
Однако при решении любых практических задач и особенно при решении неформализованных задач распространена обратная ситуация. Эксперту приходится работать в условиях неполноты и неточности знаний (данных) и, как правило, в условиях дефицита времени. Когда эксперт решает задачу, он использует методы, отличающиеся от формальных математических рассуждений. В этом случае эксперт делает правдоподобные предположения, которые он не может доказать; тем самым вопрос об их истинности остается открытым. Все утверждения, полученные на основе этих правдоподобных предположений, также не могут быть доказаны.
Итак, для того чтобы система могла делать умозаключения, основанные на здравом смысле, при работе с неполными (неточными) данными и знаниями, она должна быть способна делать предположения, а при получении новой информации, показывающей ошибочность предположений, отказываться как от сделанных предположений, так и от умозаключений, полученных на основе этих предположений. Мнение системы о том, какие факты имеют место, изменяется в ходе рассуждения, т.е. можно говорить о ревизии мнений. Таким образом, даже если рассматривать проблемную область как статическую, неполнота (и неточность) знаний и данных влечет за собой рассмотрение этой области при различных (и даже противоположных) предположениях, что, в свою очередь, приводит к представлению области в виде альтернативных пространств, соответствующих различным, возможно, противоречивым и (или) взаимодополняющим предположениям и мнениям.
Все неудачи, возникшие при поиске в одном направлении, не запоминаются при переходе к поиску в другом направлении. Та же самая причина неудачи может заново обнаруживаться и на новом направлении.
Осуществлять возврат целесообразно не к состоянию, непосредственно предшествующему данному, а к тому состоянию, которое является причиной возникновения неудачи. В используемых нами терминах причиной неудач являются предположения, т.е. недоказуемые утверждения. Поэтому при обнаружении неудачи необходимо возвращаться в состояние, где это предположение было сделано, и испытывать другое предположение.
Этот метод поиска называют поиском, направляемым зависимостью.
3.4. ПОИСК С ИСПОЛЬЗОВАНИЕМ НЕСКОЛЬКИХ МОДЕЛЕЙ
Все методы поиска, рассмотренные до сих пор, использовали при представлении проблемной области какую-то одну модель, т.е. рассматривали область с какой-то одной точки зрения. При решении сложных задач в условиях ограниченных ресурсов использование нескольких моделей может значительно повысить мощность системы. Объединение в одной системе нескольких моделей дает возможность преодолеть следующие трудности.
· переход с одной модели на другую позволяет обходить тупики, возникающие при поиске в процессе распространения ограничений.
· использование нескольких моделей позволяет в ряде случаев уменьшить вероятность потери хорошего решения (следствие неполного поиска, вызванного ограниченностью ресурсов) за счет конструирования полного решения из ограниченного числа частичных кандидатов путем их расширения и комбинации.
· наличие нескольких моделей позволяет системе справляться с неточностью (ошибочностью) данных.
Следует отметить, что использование нескольких моделей требует дополнительных знаний о том, как создавать и объединять различные точки зрения.
3.5. ВЫБОР МЕТОДА РЕШЕНИЯ ЗАДАЧ
Выбор метода решения задачи зависит прежде всего от сложности задачи, которая определяется особенностями проблемной области и требованиями, предъявляемыми пользователем к решению задачи. Для преодоления трудностей, вызванных большим пространством поиска, используются методы, основанные на введении иерархии пространств (конкретных, абстрактных и метапространств). Простейший из этих методов основывается на факторизуемости пространства решений, что позволяет производить раннее отсечение. Метод обеспечивает получение всех решений. Если пространство поиска не удается факторизовать, но при этом не требуется получать все решения или выбирать лучшее, то могут быть применены методы, использующие иерархию однородных абстрактных пространств. Если пространство поиска таково, что любая задача может быть сведена к известной заранее последовательности подзадач, то используется фиксированное абстрактное пространство.
Эффективность этого метода определяется возможностью использовать безвозвратную стратегию. В случае, если подзадачи взаимозависимы, т.е. для решения некоторой подзадачи может требоваться информация, получаемая другой подзадачей, и подзадачи не могут быть упорядочены, целесообразно применять принцип наименьших свершений. Этот подход позволяет приостанавливать решение подзадачи, для которой недостает информации, переходить к решению другой подзадачи и возвращаться к исходной задаче, когда отсутствующая информация станет доступной. (поиск в иерархии пространстве)
Для преодоления трудностей, вызванных неполнотой и (или) неточностью данных (знаний), используют вероятностные, размытые и точные методы. Все эти методы основываются на идее увеличения надежности путем комбинирования фактов и использования метазнаний о возможностях комбинирования фактов.
Для преодоления неадекватности модели проблемной области используются методы, ориентированные на использование нескольких моделей. Эти методы позволяют объединить возможности различных моделей, описывающих проблемную область с различных точек зрения. Кроме того, использование нескольких моделей позволяет уменьшить вероятность потери хорошего решения, несмотря на неполноту поиска, вызванную ограниченностью вычислительных ресурсов.
Похожие работы
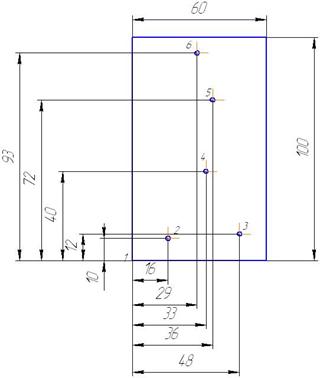
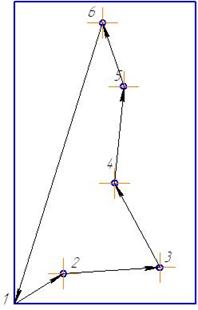
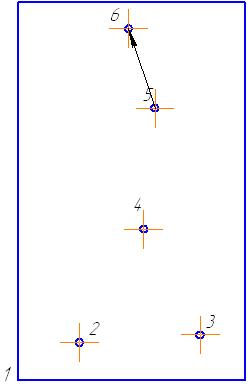
... 0 Так как нет отрицательных оценок ∆j, значит выполняется признак оптимальности и не вводились искусственные переменные, то получено оптимальное решение. Ответ: Максимальное значение функции Fmax =400 достигается в точке с координатами: =0 =8 =20 =0 =0 =96 Задача №2 (Метод Литтла) Найти кратчайший путь в графе, заданном графически в виде чертежа, методом Литтла. Из ...
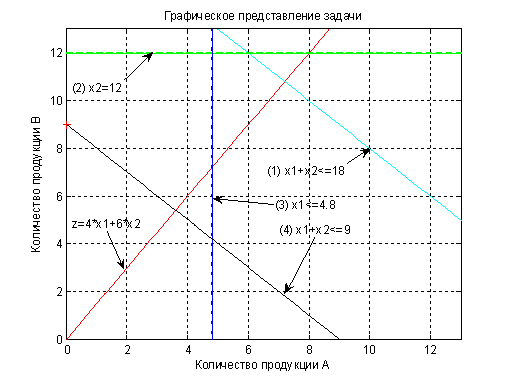
... наибольшую прибыль? Группа оборудования, штук для производства единицы продукции Прибыль, грн 1 2 3 4 А 1 0 5 3 4 В 1 1 0 2 6 Построение математической модели Для реализации графического метода решения задач линейного программирования необходимо определить целевую функцию: Z=4*x1+6*x2, где Z→max – целевая функция, x1 – количество изготовленной ...
... способами. Проверяя правильность хода решения, мы тем самым убеждаемся и в правильности результата. Второй способ проверки результата заключается в получении того же результата применением другого метода решения задачи, поэтому полезно всегда задавать решающему вопрос: "Нельзя ли тот же результат получить иначе?" Иными словами, стоит последовать совету: "Решите задачу другим способом". Если при ...
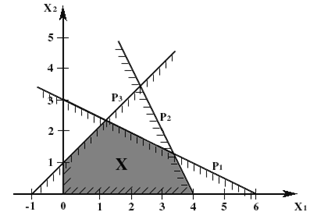
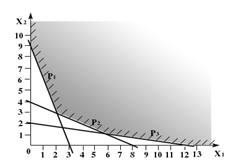
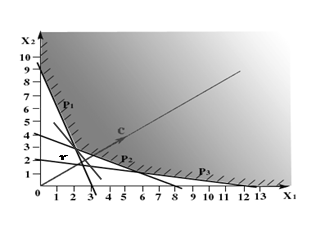
... ограничения несовместны, множество планов пусто и задача ЛП решения не имеет. Рис. 1.4 Рис. 1.5 Рис. 1.6 2. Симплекс-метод 2.1 Идея симплекс-метода Рассмотрим универсальный метод решения канонической задачи линейного программирования , , , с n переменными и m ограничениями-равенствами, известный как симплекс-метод. Множество планов канонической задачи – ...
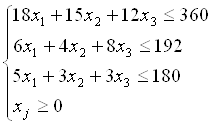

0 комментариев