Навигация
Визначимо (за допомогою ЕОМ) амплітудно-частотну (АЧХ) та фазово-частотну (ФЧХ) характеристики системи
1.2. Визначимо (за допомогою ЕОМ) амплітудно-частотну (АЧХ) та фазово-частотну (ФЧХ) характеристики системи.
1.3. Розкладемо функцію ![]() в ряд Фур’є і визначимо (за допомогою ЕОМ) параметри гармонік в розкладенні.
в ряд Фур’є і визначимо (за допомогою ЕОМ) параметри гармонік в розкладенні.
1.4. Визначимо (за допомогою ЕОМ) рішення ![]() диференціального рівняння руху механичної системи для випадку, коли збурююча сила
диференціального рівняння руху механичної системи для випадку, коли збурююча сила ![]() задається кусочно-лінійною функцією (“точне” рішення).
задається кусочно-лінійною функцією (“точне” рішення).
Розглянемо також випадок, коли сила ![]() задається сумою
задається сумою ![]() гармонік. При цьому встановимо, при якому раціональному значенні
гармонік. При цьому встановимо, при якому раціональному значенні ![]() =
=![]() функція
функція ![]() визначається з 5% точністю (по відношенню до “точного рішення”).
визначається з 5% точністю (по відношенню до “точного рішення”).
Проаналізуємо характер коливального процесу при різних значеннях ![]() <
<![]() .
.
1.5. Користуючись АЧХ и ФЧХ системи та знайденими параметрами гармонік у розкладенні сили ![]() , побудуємо (за принципом суперпозиції) аналітичне рішення
, побудуємо (за принципом суперпозиції) аналітичне рішення ![]() диференціального
рівняння, руху механічної системи.
диференціального
рівняння, руху механічної системи.
При цьому встановимо, при якому раціональне значені ![]() аналітичне рішення визначається з 5% точністю по відношенню до “точного” рішення.
аналітичне рішення визначається з 5% точністю по відношенню до “точного” рішення.
Співставлення рішень будемо проводити для контрольного моменту часу ![]() , який рекомендується вибирати із умови:
, який рекомендується вибирати із умови: ![]() .
.
2. Складання диференціального рівняння вимушених коливань механічної системи.
Рівняння вимушених коливань заданої механічної системи (рис.1) складемо за допомогою рівняння Лагранжа ІІ-го роду:
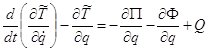 , ( )
, ( )
де ![]() і
і ![]() - узагальнена координата та швидкість,
- узагальнена координата та швидкість, ![]() і
і ![]() - кінетична і потенціальна енергії системи відповідно,
- кінетична і потенціальна енергії системи відповідно, ![]() - функція розсіювання,
- функція розсіювання, ![]() - узагальнена непотенціальна сила.
- узагальнена непотенціальна сила.
Складемо вираз кінетичної енергії системи в її довільному положенні, враховуючи, що тіло 1 виконує поступальний рух, а тіла 2 і 3 – обертальний рух; при цьому швидкості усіх тіл виразимо через узагальнену швидкість ![]() :
:
![]() ;
;
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;
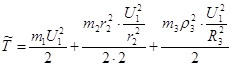 =
= 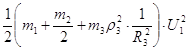 .
.
У виразі ![]() та
та ![]() - моменти інерції тіл 2 і 3 відносно центральної осі.
- моменти інерції тіл 2 і 3 відносно центральної осі.
Позначимо коефіцієнт ![]() =
=![]() , де
, де ![]() - зведена маса системи. Тоді:
- зведена маса системи. Тоді:
![]()
![]()
![]() . (
)
. (
)
Складемо вираз потенціальної енергії системи: ![]() , де
, де ![]() - потенціальна енергія сил ваги, а
- потенціальна енергія сил ваги, а ![]() - потенціальна енергія сил пружності, що діють на тіла системи.
- потенціальна енергія сил пружності, що діють на тіла системи.
Обчислемо потенціальну енергію системи в її довільному положенні як роботу потенціальних сил на переміщенні системи із довільного положення в положення статичної рівноваги:
![]() ;
;
![]() ,
,
де ![]() ;
; ![]()
![]()
![]() ;
;
тут ![]() ,
, ![]() - статичні подовження пружин;
- статичні подовження пружин; ![]() ,
, ![]() - зміна довжини відповідної пружини при відхиленні системи від стану статичної рівноваги;
- зміна довжини відповідної пружини при відхиленні системи від стану статичної рівноваги; ![]() ,
,![]() - подовження пружини в довільному положенні системи.
- подовження пружини в довільному положенні системи.
Врахуємо, що 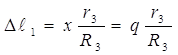 ,
, ![]() =
=![]() , а в стані статичної рівноваги
, а в стані статичної рівноваги ![]() .
.
Вираз потенціальної енергії системи та її похідної мають вигляд:
 ;
;
![]() .
.
При рівновазі системи (![]() ) маємо:
) маємо:
![]() , тобто
, тобто ![]() .
.
Тоді вираз потенціальної енергії системи приймає вигляд:
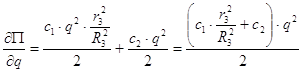 =
=![]() ,
( )
,
( )
де ![]() =
=![]() .
.
Функцію розсіювання ![]() будемо вважати залежною від узагальненої швидкості
будемо вважати залежною від узагальненої швидкості ![]() , а її похідну представимо у вигляді:
, а її похідну представимо у вигляді:
![]() ,
,
де ![]() - коефіцієнт в’язкості (дисипативний коефіцієнт).
- коефіцієнт в’язкості (дисипативний коефіцієнт).
До непотенціальних сил, що діють на систему, відноситься тільки збурююча сила ![]() , можлива робота якої
, можлива робота якої ![]() ; тоді
; тоді
![]() .
.
Візьмемо відповідні похідні і складемо рівняння Лагранжа для заданої системи:
![]()
![]() ;
; 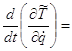
![]() ;
; ![]() 0;
0; ![]()
![]() ;
;
![]() =
=![]() ;
;
![]()
![]() ;
;
![]()
![]() ;
;
![]()
![]() ;
;
![]()
![]() , ( )
, ( )
де ![]() і
і 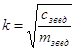 .
.
Диференціальне рівняння ( ) представляє собою неоднорідне диференціальне рівняння другого порядку відносно узагальненої координати ![]() зі сталими коефіцієнтами.
зі сталими коефіцієнтами.
Рішення задачі про дослідження вимушених коливань системи зводиться до рішення цього диференціального рівняння при заданих початкових умовах задачі. Оскільки у розглянутому випадку рух системи починається із стану статичної рівноваги, то початкові умови будуть нульовими:
при ![]() :
: ![]() ;
; ![]() .
( )
.
( )
Як відомо, аналітичне рішення рівняння ( ) складається із суми двох рішень ![]()
![]() , де
, де ![]() - загальне рішення однорідного рівняння,
- загальне рішення однорідного рівняння, ![]() - частинне рішення неоднорідного диференціального рівняння.
- частинне рішення неоднорідного диференціального рівняння.
Слід зауважити, що рішення ![]() в даному випадку (при відповідному підборі коефіцієнта
в даному випадку (при відповідному підборі коефіцієнта ![]() ) практично згасає через
) практично згасає через ![]() . Тоді получається, що при
. Тоді получається, що при ![]()
![]() .
.
Визначимо чисельні значення параметрів системи та коефіцієнтів в рівнянні ( ):
![]() =
=![]() = 0,2 + 0 +
= 0,2 + 0 +![]() = 0,2 + 0,056 = 0,256т;
= 0,2 + 0,056 = 0,256т;
![]() =
=![]() =
= ![]() + 10 = 3,56 + 10 = 13,6кН.м –1;
+ 10 = 3,56 + 10 = 13,6кН.м –1;
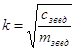
![]() =7,29с –1;
=7,29с –1; ![]()
![]() =0,861с;
=0,861с;
![]()
![]()
![]()
![]() = 0,456кН.с.м –1;
= 0,456кН.с.м –1;
![]() =
=![]() =0,891с –1.
=0,891с –1.
Для перевірки вірності визначення коефіцієнту ![]() рекомендується підрахувати значення співмножника
рекомендується підрахувати значення співмножника ![]() в рішенні
в рішенні ![]() при
при ![]() =5.0,861 = 4,31с:
=5.0,861 = 4,31с:
![]() .
.
Таке значення співмножника (наближене до нуля) в рішенні ![]() підтверджує факт, що вільні коливання системи на цей момент часу практично згасають; значить коефіцієнт
підтверджує факт, що вільні коливання системи на цей момент часу практично згасають; значить коефіцієнт ![]() знайдено вірно.
знайдено вірно.
Похожие работы
... ї зони та обмеження доступу до неї людей. На підприємстві згідно з вимогами законодавчих та інших нормативно-правових актів з питань захисту населення і територій від надзвичайних ситуацій та охорони праці повинні бути розроблені і затверджені роботодавцем: - план попередження надзвичайних ситуацій, у якому визначаються можливі аварії та інші надзвичайні ситуації техногенного та природного ...
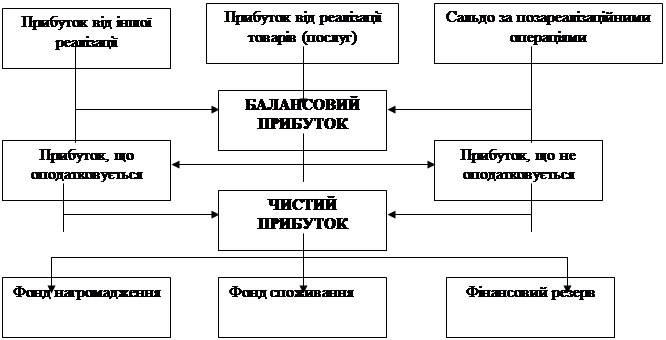
... Висновки по розділу 3 У даному розділі диплома була розроблена автоматизована інформаційна система розрахунку прибутку на гірничо-збагачувальному підприємстві. Дана система була розроблена для підвищення ефективності роботи підприємства. В основу алгоритмів обробки даних покладені методи математичної статистики й оптимізаційні моделі. Для проектування і реалізації автоматизованої інформаційної ...
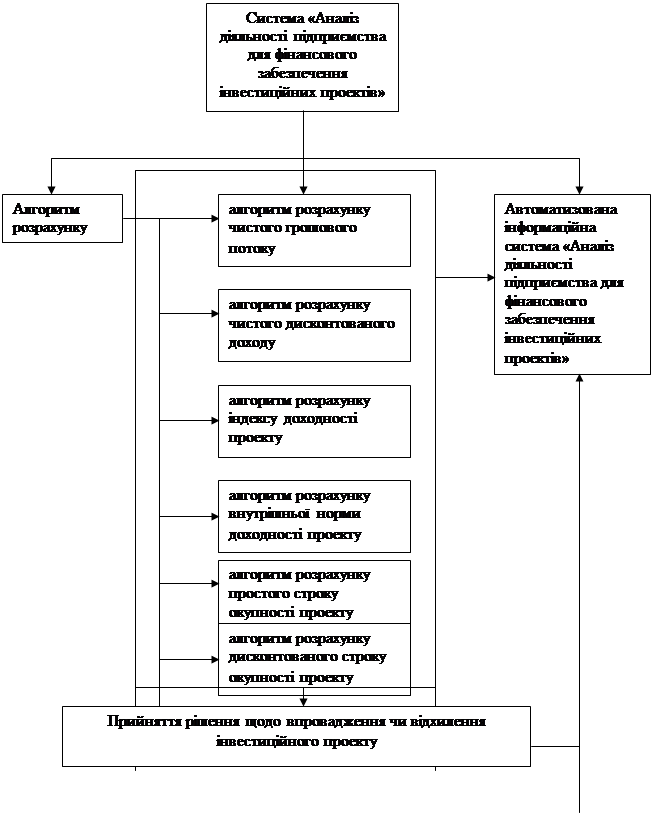
... »; 5) підсистема «Розрахунок чистого дисконтованого доходу»; 6) підсистема «Розрахунок індексу доходності проекту». Рис. 3.2. Структура інформаційної системи «Аналіз діяльності підприємства для фінансового забезпечення інвестиційних проектів» Далі приймається рішення щодо впровадження чи відхилення інвестиційного проекту. Усі ...
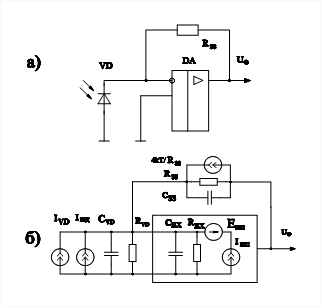
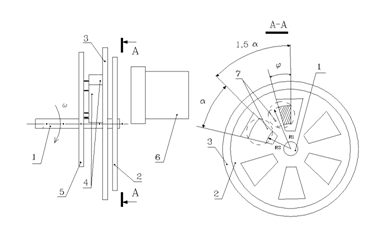
... дипломного проекту. Рисунок 3.1 – Схема електрична структурна пристрою контролю середнього значення кутової швидкості 4. Розробка принципової схеми комп’ютеризованої вимірювальної системи параметрів електричних машин з газомагнітним підвісом 4.1 Аналіз лінійного фотоприймача Фотоелектричні перетворювачі площа-напруга (ППН) використовуються у багатьох пристроях, таких як перетворювач ...







0 комментариев