Навигация
Простейшая задача оптимального быстродействия
17888
знаков
0
таблиц
3
изображения
1. Простейшая задача оптимального быстродействия.
Пусть точка движется по прямой в соответствии с законом
(3.1)
где х - координата. Требуется найти управление и, переводящее точку из начального положения в начало координат за минимальное время Т (задача оптимального быстродействия). При этом скорость точки в конце траектории должна быть нулевой, а управление - удовлетворять условию
.
Применим к сформулированной задаче принцип максимума Понтрягина . Введем фазовые переменные 
. Тогда движение управляемого объекта описывается системой двух дифференциальных уравнений первого порядка:
(3.2)
Начальное положение
при t0=0 и конечное положение (0, 0) фиксированы, а конечный момент времени Т не фиксирован.
В обозначениях п.п. 1, 2 в данной задаче U ==[-1, 1], f0=1, Ф=0, а функция Гамильтона имеет вид
Общее решение сопряженной системы
легко выписывается в явном виде 
где С, D - постоянные.
Очевидно, что максимум функции Н по и
U достигается при
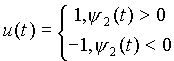
Таким образом, оптимальное управление и может принимать лишь два значения +1 .
2.Определить управление u(t) , которое дает минимум интегралу
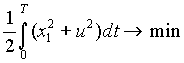, в процессе, описываемом уравнением 
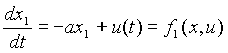(1).
Решение.
Введем дополнительную переменную
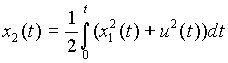(2)
Для этой переменной имеем дифференциальное уравнение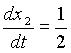 
(
(3)
с начальными условиями, получаемыми из (2), т.е. х2(0)=0. Минимизирующий функционал, используя (2), можно записать в виде I[T]=x2(T).
Построим функцию Гамильтона
Запишем сопряженную систему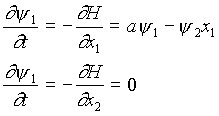 
(3)
Запишем 
Y1(Т)=0 (т.к. с1=0)
Y2(Т)=-1
Из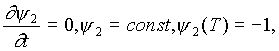 
поэтому Y2(е)=-1. Теперь функция Гамильтона запишется в виде H=-aY1x1+Y1u-0,5x12-0,5u2 .
По принципу максимума функция Н при фиксированных х1 и Y1 достигает максимума по u :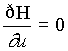 
, 
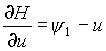, откуда 
.
Осталось решить систему уравнений (2) и (3) при условии , Y2(Т)=-1,
, 
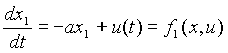с граничными условиями 
Сведем данную систему к одному уравнению относительно U.
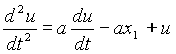
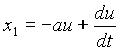
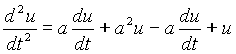
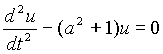
Добавим к этому уравнению граничные условия 
и решим его. Составим характеристическое уравнение к2 - (а2+1) =0, к1,2=+(-)
Найдем С1 и С2. 
С2=-с2е
. Тогда 
Используя граничные условия найдем С2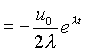
Таким образом, определено оптимальное решение
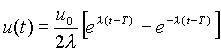
Примеры применения принципа максимума.
Похожие работы
... с нач. условием , такая что выполняется условие: -здесь достигается максимум. 2); 3). Теорема о необходимых условиях оптимальности. Если в линейной задаче быстродействия мн-ва выпуклы, -оптимальное управление, переводящее на отр. , а -соответствующая траектория, то пара удовлетворяет принципу максимума Понтрягина. 23. Применение необходимых условий оптимальности(схема и пояснения к ней). ...
... проектирования. Целью проекта является создание программного продукта (ПП), основанного на математическом пакете MatLab, реализующего математическую модель системы управления, построенной на основе оптимального закона, для системы слежения РЛС. Данный проект можно отнести к научно-исследовательской работе, которая принадлежит к типу прикладных, направленных на решение научных проблем с целью ...
... от года-x и от номера месяца в году-y следующим образом: F(x)=50-x2+10x-y2+10y. Определите, в каком году и в каком месяце прибыль была максимальной. Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету МЕТОДЫ ОПТИМИЗАЦИИ Билет № 22 1) Постановка вариационной задачи с ограничениями. Привести пример. 2) Дайте геометрическую ...
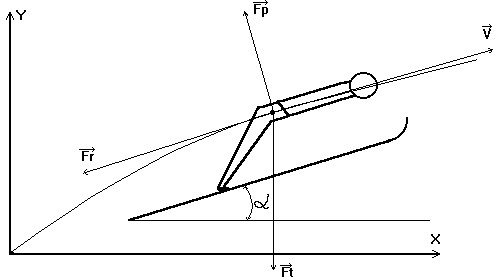
... пользы прыгунам - и действительно принесла. Положительной стороной книги является рассмотрение всех стадий прыжка, что у нас присутствует пока только в планах на будущее. Вопросам моделирования прыжка с трамплина посвящены работы Л.П.Ремизова [2,3]. Первая из них, опубликованная в советском журнале "Теория и практика физической культуры" в 1973 году, создает впечатление то ли выборки, то ли ...
0 комментариев