Навигация
Математическая модель системы слежения РЛС
Содержание. 1
Введение. 3
1 Общая теория оптимального управления. 6
1.1 Допустимые управления. 6
1.2 Основные направления в теории оптимальных процессов. 11
1.2.1 Метод динамического программирования. 12
1.2.2 Принцип максимума. 13
1.3 Программное управление. 16
1.4 Постановка задачи и способы решения. 18
2 Система оптимального управления. 24
2.1 Математическое описание электромеханической системы.. 24
2.2 Идентификация авторегрессионно-регрессионной модели. 29
2.3 Формирование ограничений. 37
2.4 Формирование оптимальных траекторий. 42
2.5 Анализ решений. 50
2.6 Общая структура системы оптимального управления. 55
2.7 Полученные результаты.. 58
3 Практическая реализация. 63
3.1 Реализация оптимального управления в среде пакета matlab. 63
3.2 Выбор микроконтроллера. 64
4 Экономическое обоснование проекта. 66
4.1 Технико-экономическая характеристика. 66
4.2 Маркетинговая ориентация. 66
4.3 оценка научно-технической результативности и социальной эффективности НИР 68
4.4 Производственный план. 74
4.4.1 Расчёт затрат на разработку. 75
4.4.2 Затраты на создание опытного образца. 77
4.4.3 Затраты на эксплуатацию.. 79
4.4.4 Ценообразование. 79
Выводы.. 80
5 Безопасность и экологичность проекта. 81
5.1 Анализ опасных и вредных факторов. 82
5.2 Мероприятия по улучшению условий труда. 83
5.2.1 Помещения и их освещение. 83
5.2.2 Уровень шума и вибрация. 85
5.2.3 Параметры микроклимата. 86
5.2.4 Защита от электромагнитных и электростатических полей. 87
5.2.5 Электробезопасность. 90
5.2.6 Дисплейные терминалы и ПЭВМ в составе АРМ.. 91
5.2.7 Организация и оборудование рабочих мест с ВДТ и ПЭВМ.. 93
5.2.8 Требования к организации режима труда и отдыха при работе на АРМ.. 95
5.3 Устойчивость проекта к чрезвычайным ситуациям. 97
5.4 Экологичность проекта. 98
5.5 Выводы.. 99
Заключение. 100
Приложение. 101
Блок-схема файл-функции OPTIMUM_CONTR.. 101
Введение
Во многих областях техники и технологии приходится иметь дело со следующей задачей, которую можно трактовать как задачу «сопровождения цели». Причем, наблюдаемый процесс в некоторых случаях является детерминированным, т.е. полностью определенным, а в некоторых — не известным, но и в том и в другом случае в нем присутствует шум — случайная составляющая. Заданием для управляемого объекта служит движение другого объекта — задающего. Таким образом, задача слежения сводится к задаче перевода системы из начального состояния в наперед заданное состояние, которое определяется фазовым состоянием наблюдаемой системы.
В начальный момент времени t0 объект находится в фазовом состоянии x0; требуется выбрать такое управление u(t), которое переведет объект в заранее заданное конечное фазовое состояние x1 (отличное от x0). При этом нередко бывает, что начальное состояние x0 заранее неизвестно.
Такое управление часто осуществляется человеком (оператором), который следит за приборами и старается выбирать управление, поддерживающее объект в требуемом рабочем режиме.
Однако в современных условиях высокого развития техники оператор зачастую не может успешно справиться с этой задачей ввиду сложности поведения объекта, большой быстроты протекания процессов и т. п. Поэтому чрезвычайно важно создать такие приборы, которые сами, без участия человека, управляли бы работой объекта (например, в случае выхода объекта из рабочего состояния возвращали бы его в это рабочее состояние). Такие приборы сейчас очень распространены в технике, их изучением занимается теория автоматического управления.
В общем случае на вход регулятора подаются фазовые координаты объекта. Регулятор конструируется так, что его выходная величина u, поданная на вход объекта, нужным образом управляет работой объекта (т. е., например, возвращает объект в рабочее состояние, если он почему-либо вышел из этого состояния).
Обычно требуется, чтобы переходный процесс (т. е. процесс перехода из начального фазового состояния x0 в предписанное конечное состояние x1) был в определенном смысле «наилучшим», например, чтобы время перехода было наименьшим или чтобы энергия, затраченная в течение переходного процесса, была минимальной и т. п. Такой «наилучший» переходный процесс называется оптимальным процессом.
Разумеется, желательно, чтобы регулятор не просто возвращал объект в рабочее состояние, а делал это наилучшим образом, например, в смысле быстродействия (т.е. возвращал объект в рабочее состояние за кратчайшее время). В связи с этим в теории автоматического управления рассматриваются весьма различные (по устройству и степени сложности) регуляторы. Рассмотрение регуляторов, которые применялись на практике и изучались в руководствах по автоматическому регулированию до возникновения теории оптимальных процессов, приводит к выводу, что уменьшение времени переходного процесса связано с усложнением конструкции регулятора; поэтому, усложняя конструкцию регулятора, можно лишь приближаться к «идеальному», «оптимальному» регулятору, который во всех случаях осуществляет переходный процесс за кратчайшее время.
Одной из важных заслуг теории оптимальных процессов является установление существования оптимальных регуляторов и создание математического аппарата, позволяющего рассчитывать такие регуляторы. Оптимальные регуляторы существенно отличаются от тех, которые до сих пор изучались в теории автоматического управления.
На данном уровне развития техники и технологии для такого рода управления в большинстве случаев используются стандартные регуляторы (например, ПИД-регуляторы). Во многих случаях их применение может быть оправдано и их работа удовлетворяет поставленным целям управления, но существуют ситуации, в которых применение таких регуляторов не дает необходимого результата. Использование ПИД-регуляторов может оказаться нецелесообразным в случае ограничений на управление. В такой ситуации, система в целом оказывается существенно нелинейной и классические приемы управления в этом случае не приемлемы.
В данной работе рассматривается система, состоящая из двух электроприводов, один из которых является ведущим, а другой — ведомым. Ведомый двигатель должен двигаться синхронно с ведущим. Система должна отрабатывать заданную траекторию с необходимой точностью и максимальным быстродействием.
1 Общая теория оптимального управления 1.1 Допустимые управления
Наиболее перспективным решением экстремальных задач является их решение на основе теории принципа максимума Понтрягина. В данной работе ставилась задача оптимизации по времени, для чего и были использованы методы оптимального управления, предложенные Л.С. Понтрягиным, В.Г. Болтянским, Р.В. Гамкрелидзе. [1]
Задача оптимального быстродействия заключается в отыскании такого управления u(t), для которого фазовая траектория x(t) проходит через точку x1 и переход из х0 в х1 осуществляется за кратчайшее время. Такое управление u(t) называется оптимальным управлением (в смысле быстродействия); точно так же соответствующую траекторию x(t), по которой фазовая точка за кратчайшее время переходит из состояния x0 в состояние x1 называется оптимальной траекторией.
Обычно управляющие параметры u1,..., ur не могут принимать совершенно произвольные значения, а подчинены некоторым ограничениям. Это обусловлено техническими характеристиками реальных объектов управления, а также конструкцией регулирующих устройств.
Например, для двигателя постоянного тока (ДПТ), одним из управляющих параметров служит напряжение якоря; однако именно в силу конструктивных особенностей ДПТ этот параметр подчинен ограничениям указанного типа. Так, значение этого параметра не может принимать сколь угодно большое значение.
Для объекта, содержащего r управляющих параметров u1, u2, ..., ur, в приложениях часто встречается случай, когда эти параметры могут произвольно меняться в следующих пределах:
![]()
Т. е. каждая из величин u1, u2, ..., ur представляет собой отдельный управляющий параметр, область изменения которого не зависит от значений остальных управляющих параметров и задается неравенствами
![]() (1.1)
(1.1)
Заметим, что при r = 2 точки ![]() , координаты которых подчинены неравенствам (1.1), заполняют прямоугольник (рисунок 1.1); при r = 3 неравенства (1.1) определяют в пространстве переменных u1, u2, u3 прямоугольный параллелепипед.
, координаты которых подчинены неравенствам (1.1), заполняют прямоугольник (рисунок 1.1); при r = 3 неравенства (1.1) определяют в пространстве переменных u1, u2, u3 прямоугольный параллелепипед.
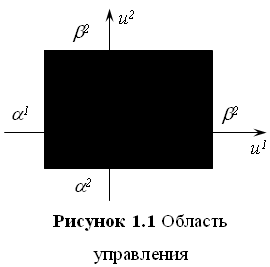
В общем случае будем считать, что в соответствии с конструкцией объекта и условиями его эксплуатации задано в пространстве переменных u1, ..., ur некоторое множество U и управляющие параметры u1, u2, ..., ur должны в каждый момент времени принимать лишь такие значения, чтобы точка ![]() принадлежала множеству U. Т. е. разрешается рассматривать лишь такие управления u(t), что
принадлежала множеству U. Т. е. разрешается рассматривать лишь такие управления u(t), что ![]() для любого t. Множество U называется областью управления.
для любого t. Множество U называется областью управления.
Область управления U, в общем случае, может быть не только параллелепипедом, но может иметь более или менее геометрически сложный характер, так как благодаря конструкции объекта между управляющими параметрами могут существовать некоторые связи, выражаемые некоторыми уравнениями или неравенствами. Указанные области управления должны входить в математическое описание объекта.
Для технических задач важен случай замкнутого множества U, т.е. случай, когда точка ![]() может находиться не только внутри множества, но и на его границе. Т.е. для «рулей» допустимы и их крайние положения.
может находиться не только внутри множества, но и на его границе. Т.е. для «рулей» допустимы и их крайние положения.
Для полного осмысления данного вопроса необходимо сделать еще одно, очень важное, предположение о характере управлений. Возможны несколько случаев представления управляющих воздействий. А именно, в одном случае, когда это позволяет точность представления, можно предполагать, что «рули», положения которых характеризуются управляющими параметрами u1, u2, ..., ur, безынерционны, так что есть возможность, если нужно, мгновенно переключать эти «рули» из одного положения в другое, т. е. менять скачком значения управляющих параметров u1, u2, ..., ur в пределах области управления.
В другом случае, когда точность расчетов не допускает таких приближений нужно предполагать, что управляющие воздействия не могут меняться скачкообразно на сколь угодно большую величину, т.е. существует ограничение не только на значение управляющего параметра, но и на скорость изменения этого параметра. В этом случае достаточно написать ![]() , где
, где ![]() — скорость изменения управляющего параметра, и принять за управляющий параметр величину
— скорость изменения управляющего параметра, и принять за управляющий параметр величину ![]() . Т. о. существует ограничение вида
. Т. о. существует ограничение вида
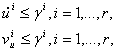 (1.2)
(1.2)
что несколько осложняет поиск оптимального управления.
Всякий реальный процесс обладает некоторой «инерционностью», но во всяком реальном управляемом объекте всегда можно найти такие управляющие параметры, которые, в пределах заданной точности, можно считать безынерционными.
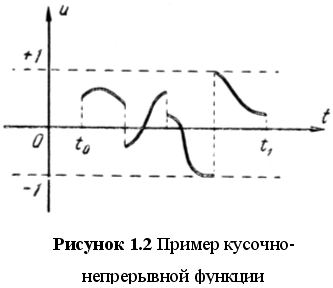
В соответствии с этим будут рассматриваться не только непрерывные, но и кусочно-непрерывные управления u(t). Класс кусочно-непрерывных управлений хорош тем, что, во-первых, позволяет получить точное математическое решение оптимальной задачи для широкого класса примеров, а во-вторых, наиболее интересен и удобен для технической реализации.
Необходимо уточнить, что функция ![]() со значениями в области управления U называется кусочно-непрерывной, если она состоит из конечного числа непрерывных кусков (рисунок 1.2), т.е. непрерывна для всех рассматриваемых t, за исключением лишь конечного числа моментов времени, где функция u(t) может терпеть разрывы первого рода; последнее означает, что в каждой точке разрыва t предполагается существование конечных пределов слева и справа:
со значениями в области управления U называется кусочно-непрерывной, если она состоит из конечного числа непрерывных кусков (рисунок 1.2), т.е. непрерывна для всех рассматриваемых t, за исключением лишь конечного числа моментов времени, где функция u(t) может терпеть разрывы первого рода; последнее означает, что в каждой точке разрыва t предполагается существование конечных пределов слева и справа:
![]()
Значение кусочно-непрерывного управления u(t) в точке разрыва не играет сколько-нибудь существенной роли. Однако для определенности будет удобно предполагать, что управление u(t) в точках разрыва непрерывно справа, т. е. что в каждой точке разрыва t значение управления u(t) равно пределу справа:
![]()
Кроме того, предполагается, что каждое рассматриваемое управление u(t) непрерывно в концах отрезка ![]() на котором оно задано, т. е. что все его точки разрыва, если они есть, расположены на интервале
на котором оно задано, т. е. что все его точки разрыва, если они есть, расположены на интервале ![]() .
.
Допустимым управлением называют всякую кусочно-непрерывную функцию ![]() со значениями в области управления U, непрерывную справа в точках разрыва и непрерывную в концах отрезка
со значениями в области управления U, непрерывную справа в точках разрыва и непрерывную в концах отрезка ![]() на котором она задана.
на котором она задана.
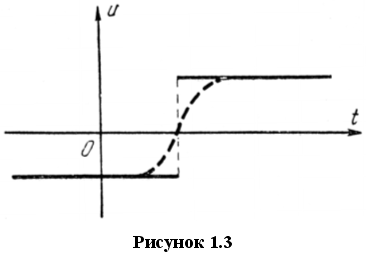
Оптимальные управления оказываются, в большинстве случаев, разрывными (т.е. содержащие скачки и переключения). Если разрывная функция, график которой изображен на рисунке 1.3 сплошной линией, представляет собой оптимальное управление, то, «сгладив» эту функцию (пунктир на рисунке 1.3), будет получена близкая к ней непрерывная функция. Но какая бы «близкая» к оптимальному управлению непрерывная функция ни была, всегда можно выбрать «сглаживающий» кусок еще более крутым и получить непрерывную функцию, еще более близкую к оптимальному управлению. Таким образом, в классе непрерывных функций просто не будет наилучшего, оптимального управления, а предельным случаем является кусочно-непрерывная функция, которая и является оптимальным управлением.
1.2 Основные направления в теории оптимальных процессовТеория оптимальных процессов базируется на методе динамического программирования, разработанного Р. Беллманом, а также на принципе максимума Понтрягина. Для линейных систем принцип максимума был доказан Р.В. Гамкрелидзе. Кроме того, ему принадлежит теорема о конечности числа переключений. Доказательство принципа максимума для нелинейных систем принадлежит В.Г. Болтянскому.
Далее кратко рассмотрим общие принципы метода динамического программирования и принципа максимума.
1.2.1 Метод динамического программирования
Для получения уравнения Беллмана и формулировки теоремы, являющейся сущностью метода динамического программирования автором данной теории были выдвинуты следующие гипотезы.
Гипотеза 1.1. Какова бы ни была отличная от x1 точка x фазового пространства, существует оптимальный (в смысле быстродействия) процесс перехода из точки x в точку x1.
Время, в течение которого осуществляется оптимальный переход из точки x в точку x1, обозначим через Т(х). И пусть
w(x) = — T(x).
Гипотеза 1.2. Функция w(x) непрерывна и всюду, кроме точки x1, имеет непрерывные частные производные
![]()
На основе этих гипотез была сформулирована и доказана теорема 1.1.
Теорема 1.1. Если для управляемого объекта, описываемого уравнением ![]() , и предписанного конечного состояния x1 выполнены гипотезы 1 и 2, то имеют место соотношения (1.3) и (1.4) (оптимальность понимается в смысле быстродействия).
, и предписанного конечного состояния x1 выполнены гипотезы 1 и 2, то имеют место соотношения (1.3) и (1.4) (оптимальность понимается в смысле быстродействия).
![]() для всех точек x ¹ x1 и u,
для всех точек x ¹ x1 и u,
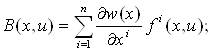 (1.3)
(1.3)
![]()
для любого оптимального процесса (u(t), x(t)). (1.4)
Эта теорема и составляет сущность метода динамического программирования.
Метод динамического программирования (1.3), (1.4) содержит некоторую информацию об оптимальных процессах и потому может быть использован для их разыскания. Однако он имеет ряд неудобств. Во-первых, применение этого метода требует нахождения не только оптимальных управлений, но и функции w(x) так как эта функция входит в соотношения (1.3), (1.4). Во-вторых, уравнение Беллмана представляет собой уравнение в частных производных относительно функции w. Указанные обстоятельства сильно затрудняют возможность пользования методом динамического программирования для отыскания оптимальных процессов в конкретных примерах. Но самым главным недостатком этого метода является предположение о выполнении гипотез 1.1 и 1.2. Ведь оптимальные управления и функция w заранее неизвестны, так что гипотезы 1.1 и 1.2 содержат предположение о неизвестной функции, и проверить выполнение этих гипотез по уравнениям движения объекта невозможно.
Далее кратко излагается сущность принципа максимума, который является значительно более удобным средством для отыскания оптимальных процессов, чем метод динамического программирования.
1.2.2 Принцип максимумаГипотеза 1.3. Функция w(x) имеет при x ¹ x1 вторые непрерывные производные ![]() , а функции
, а функции ![]() — первые непрерывные производные
— первые непрерывные производные ![]() .
.
Теорема 1.2. Предположим, что для рассматриваемого управляемого объекта, описываемого уравнением
![]() (1.5)
(1.5)
И предписанного конечного состояния x1 выполнены гипотезы 1.1, 1.2 и 1.3. Пусть ![]() , — некоторый процесс, переводящий объект из начального состояния x0 в состояние x1. Введем в рассмотрение функцию H, зависящую от переменных
, — некоторый процесс, переводящий объект из начального состояния x0 в состояние x1. Введем в рассмотрение функцию H, зависящую от переменных ![]() и некоторых вспомогательных переменных
и некоторых вспомогательных переменных ![]()
![]() ........................................................................ (1.6)
........................................................................ (1.6)
С помощью этой функции H запишем следующую систему дифференциальных уравнений для вспомогательных переменных:
![]() (1.7)
(1.7)
Тогда, если процесс ![]() является оптимальным, то существует такое нетривиальное решение
является оптимальным, то существует такое нетривиальное решение ![]() , системы (1.7), что для любого момента t,
, системы (1.7), что для любого момента t, ![]() , выполнено условие максимума
, выполнено условие максимума
![]() (1.8)
(1.8)
и условие
![]()
Эта теорема значительно удобнее для отыскания оптимальных процессов, чем метод динамического программирования. Однако в приведенной здесь форме принцип максимума страдает тем же недостатком, что и метод динамического программирования: он выведен в предположении дифференцируемости (и даже двукратной) функции w(x), а эта функция, как уже отмечалось, в действительности не является всюду дифференцируемой.
Однако принцип максимума доставляет достаточную информацию для решения поставленной задаче оптимального управления.
Благодаря работам Р.В. Гамкрелидзе, принцип максимума был доказан для линейных систем. Им были доказаны теоремы существования, единственности и теорема о числе переключений.
В данном случае функция Н принимает вид
![]() (1.9)
(1.9)
Выражение (1.7) в векторной форме записывается в виде
![]() (1.10)
(1.10)
а соотношение (1.8) принимает в данном случае вид
![]() (1.11)
(1.11)
Теорема 1.3 (теорема существования). Область управляемости является выпуклым открытым множеством фазового пространства Х; для любой точки х0, принадлежащей области управляемости, существует оптимальное управление, переводящее точку х0 в начало координат.
Примечание: Множество G называется открытым, если для каждой его точки можно найти шар с центром в этой точке, целиком принадлежащий множеству G, иначе говоря, множество G открыто, если к нему не причисляется ни одна точка его границы.
Областью управляемости объекта называется множество всех тех точек х0 фазового пространства X, из которых возможно при помощи какого-либо допустимого управления попасть в начало координат. Само начало координат тоже причисляется к области управляемости.
Теорема 1.4 (теорема о числе переключений). Для каждого нетривиального решения y(t) уравнения (1.10) соотношение (1.11) однозначно определяет допустимое управление u(t); при этом оказывается, что функция u(t) кусочно-постоянна и ее значениями являются лишь вершины многогранника U.
Таким образом, функция u(t) кусочно-постоянна, принимает значения в вершинах многогранника U и определена однозначно. Каждую точку разрыва оптимального управления называют точкой переключения.
В общем случае число переключений хотя и конечно, но может быть произвольным. Однако существует один важный для приложений случай, когда число переключений допускает точную оценку. Этот случай рассматривается в теореме принадлежащей А.А. Фельдбауму. В этой теореме говорится (упрощенно), что каждая из функций ![]() кусочно-постоянна и имеет не более n—1 переключений (т.е. не более n интервалов постоянства), где n — порядок системы.
кусочно-постоянна и имеет не более n—1 переключений (т.е. не более n интервалов постоянства), где n — порядок системы.
Таким образом, принцип максимума является наиболее удобным для решения задачи об оптимальном быстродействии.
1.3 Программное управлениеСегодня оборудование с программным управлением распространено весьма широко, начиная от компаний, входящих в TOP 500 Fortune в больших промышленных зонах, и заканчивая малыми предприятиями частного бизнеса. Действительно весьма трудно найти ту область машиностроения, где еще не используются уникальные возможности этого оборудования. Поэтому каждый специалист в области машиностроения должен хорошо представлять то, что дает производству применение этого весьма интеллектуального оборудования.
Программное управление технологическим оборудованием и процессами охватывает управление движением машин, механизмов, транспортных средств и изменением физических и химических параметров технологического процесса.
Программное управление — это управление режимом работы или состоянием объекта по заранее заданной программе. При автоматическом программном управлении технологическим оборудованием, соответствующая алгоритму программа записывается в память управляющего устройства с последующим автоматическим считыванием и преобразованием в управляющие сигналы.
Программное управление может быть реализовано на различных классах вычислительных машин, начиная от микроЭВМ и заканчивая мощными вычислительными системами. Каждый из этих классов накладывает на алгоритмы некоторые ограничения, которые необходимо учитывать при разработке алгоритмического обеспечения.
Разрабатываемый алгоритм ориентируется для использования в микроконтроллерах, что накладывает особые ограничения на полученный алгоритм.
Необходимо отметить, что микроконтроллеры выполняют операции для дискретного времени и дискретных величин. Вычисления осуществляются с конечной точностью и за конечное время.
Следует также учитывать тот факт, что микроконтроллеры не вычисляют точных значений интегралов и производных, но могут оценивать их значения в конечных разностях, т.е. с помощью численных методов.
Еще одним из важнейших условий, необходимым для успешной практической реализации, является необходимость учитывать отношение стоимости и мощности микроконтроллеров, которые будут использоваться в производстве.
Таким образом, после определения алгоритма оптимального управления для его реализации на реальном микроконтроллере необходимо выполнить оптимизацию по количеству операций, необходимых для проводимых вычислений, а также выполнить оценку точности вычислений. Оценка точности вычислений налагает ограничения на разрядность используемых микроконтроллеров, что в свою очередь сказывается на стоимости устройства в целом. Поэтому, изначально, алгоритм должен ориентироваться на элементарные операции сложения и вычитания, а также логические операции при переключении режимов.
При наличии сложных функциональных зависимостей, необходимо выполнить оценку их табулируемости для обеспечения высокого быстродействия работы алгоритма.
1.4 Постановка задачи и способы решенияВ производстве всегда существовала проблема, сущность которой заключалась в переводе системы из некоторого начального фазового состояния в некоторое заранее заданное конечное состояние. Причем точность перехода должна быть максимальной, а время — минимальным.
В настоящее время эту проблему решает теория автоматического управления на базе стандартных регуляторов. Примером может служить широко распространенный ПИД-регулятор, на базе которого решается большой круг задач. Во многих случаях результаты, получаемы при использовании этих устройств, удовлетворяют потребностям управления. Там где не требуется очень высокое быстродействие или ограничения, накладываемые конструктивными особенностями и характеристиками реальных объектов на вид и характер переходного процесса не являются очень строгими возможно применять данные устройства.
Но с течением времени, в связи с развитием науки и техники инструменты производства все более усложняются, повышаются и требования к качеству управления. Под качеством понимается не только точность, но и быстродействие. Также возникают ситуации, в которых управление выработанное стандартными устройствами не может быть реализовано в полной мере из-за тех или иных технических характеристик объектов управления. Для удовлетворения современным запросам управления промышленные регуляторы совершенствуются и усложняются, что дает некоторый положительный результат, но приводит также и к нежелательным последствиям. А именно — с усложнением конструкции уменьшается надежность данного устройства и растет его стоимость, что, в свою очередь, тормозит внедрение его в производство.
Примером не адекватной работы устройств на базе стандартных регуляторов могут служить системы имеющие ограничения на управление. В такой ситуации, система в целом оказывается существенно нелинейной и классические приемы управления в этом случае не приемлемы и для достижения положительных результатов необходимо применять принципиально новые теории и законы, на базе которых можно получить такой вид регуляторов, который удовлетворял бы всем поставленным условиям и требованиям.
Целью данной работы является создание математической модели устройства, позволяющего адекватно управлять объектом при наличии ограничений на управление, причем главным условием ставится минимизация времени переходного процесса системы. Предполагается, что наиболее успешным и перспективным решением такого рода задач будет решение на базе теории принципа максимума Понтрягина.
В данной работе рассматривается радиолокационная установка, которая представляет собой совокупность как минимум двух синхронно вращающихся антенн, приводимых в движение электроприводами. В данной системе существует ведущий электропривод, который задает параметры вращения, и ведомый, который должен в точности повторять траекторию движения ведущего.
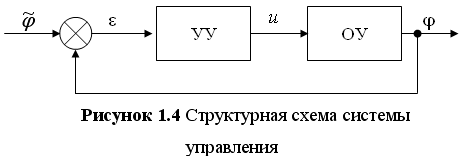
Предполагается, что тип двигателей, приводящих в движение эти антенны, не имеет для данной работы особого смысла. Сделаем следующее допущения: в данной системе есть возможность измерять в каждые заданные моменты времени положение ведущей антенны, т.е. есть возможность получать информацию о траектории ведущей антенны. Таким образом в связи со сделанными допущениями, система представляет собой совокупность двух электроприводов.
Ставится следующая задача: ведомый двигатель должен двигаться синхронно с ведущим. Система должна отрабатывать заданную траекторию с необходимой точностью и максимальным быстродействием.
В начальный момент времени оба двигателя могут быть рассинхронизированы. Конкретизируем задачу: необходимо за минимальный промежуток времени вывести ведомый двигатель на траекторию ведущего, причем в конце переходного процесса должны совпадать не только угол j, но также и скорость w, т. е., другими словами, ведомый двигатель попав на нужную траекторию, должен находиться на ней. Главным условием ставится минимизация времени переходного процесса. Таким образом ставится задача оптимально быстродействия.
Достижение указанной цели обусловлено решением следующих задач:
1. Построение оптимального программного управления системы слежения РЛС;
1.1. Построение оптимизационного функционала;
1.2. Вычисление точек переключения;
1.3. Нахождение оптимальных траекторий;
2. Моделирование полученной системы управления;
3. Проверка сделанных гипотез.
Предполагается, что процесс управления будет иметь циклический характер, так как в результате одного шага управления координаты ведущего и ведомого двигателей будут совпадать с некоторой погрешностью, которая в свою очередь будет являться начальными данными для следующего шага управления и т.д.
Запишем поставленную цель управления в виде:
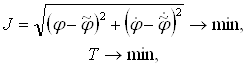 (1.12)
(1.12)
где — J, T — целевые функционалы по ошибке и времени; ![]() — выходные координаты ведомого двигателя;
— выходные координаты ведомого двигателя; ![]() — выходные координаты ведущего двигателя.
— выходные координаты ведущего двигателя.
Выходные координаты ведущего двигателя в данном случае являются заданием.
Как было сказано выше, в реальных системах всегда существуют ограничения на управление, обусловленные техническими особенностями реальных объектов. В данном случае — это ограничение на напряжение якоря двигателя. Эти условия представляют собой ограничения на величину и на скорость изменения управляющего параметра U. Таким образом эти ограничения выделяют в пространстве управлений некоторое подпространство, называемое, как было сказано выше, областью управления. Область управления представляет собой r-мерный параллелепипед.
В теории принципа максимума было доказано, что управление будет оптимальным в случае движения по граням параллелепипеда области управления. В нашем случае областью управления является прямоугольник, так как множество управлений представляет собой пространство R2. Управление будет представлять собой кусочно-непрерывную функцию.
Движение системы в фазовом пространстве должно проходить по оптимальным траекториям. Оптимальной траектория будет лишь в случае приложения оптимального управления, характер которого описан выше.
Для отыскания оптимального перехода в смысле быстродействия необходимо получить множество оптимальных траекторий. Это множество является общим решением системы уравнений, описывающих объект, при приложенном оптимальном управлении. Вид этих кривых будет описан ниже в главе 2.
Будем решать задачу в базисе ошибок.
Задавшись выражением (1.13)
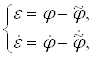 (1.13)
(1.13)
где ![]() — выходные координаты ведомой системы,
— выходные координаты ведомой системы, ![]() — выходные координаты ведущей системы, являющиеся заданием,
— выходные координаты ведущей системы, являющиеся заданием, ![]() — ошибка и скорость ошибки, можно сформулировать задачу в базисе ошибки: за минимальный промежуток времени вывести ошибку e и ее производную
— ошибка и скорость ошибки, можно сформулировать задачу в базисе ошибки: за минимальный промежуток времени вывести ошибку e и ее производную ![]() в нуль.
в нуль.
Так как оптимальное управление имеет вид кусочно-непрерывной функции имеющей точки переключения, то движение системы в базисе ошибок будет проходить по кривым, имеющим конечное число точек переключения (а соответственно и интервалов постоянства), соответствующим точкам переключения управляющего параметра. Таким образом возникает проблема нахождения моментов времени, в которые необходимо изменить значение (переключить) управляющего параметра.
Таким образом общая задача сводится к нахождению области управления, нахождению вида оптимальных траекторий и вычисление моментов времени точек переключения управляющего параметра.
В результате решения общей задачи, сформулированной выше, должен быть получен общий алгоритм функционирования системы оптимального управления, который необходимо оптимизировать для использования в микроконтроллерах.
2 Система оптимального управления
2.1 Математическое описание электромеханической системы
В данной работе рассматривается радиолокационная установка, которая представляет собой совокупность как минимум двух синхронно вращающихся антенн. В данной системе одна из антенн является ведущей — она задает параметры движения, другая — ведомая, которая должна в точности повторять траекторию движения ведущей.
Каждая из антенн представляет собой сложную электромеханическую систему, представляющую собой совокупность таких составных частей как электропривод, редуктор и собственно принимающая антенна. Основным источником механической энергии является электропривод. Редуктор служит для преобразования угловых скоростей и соответственно вращающих моментов, выдаваемых двигателем. Редукторы могут быть зубчатые (в том числе червячные) или гидравлические.
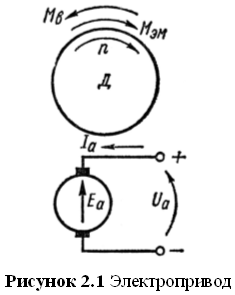
Напомним, что в разделе 1.5 были сделаны следующие допущения: в данной системе есть возможность измерять в каждые заданные моменты времени положение ведущей антенны, т.е. есть возможность получать информацию о траектории ведущей антенны; тип двигателя, приводящего в движение антенны является не существенным для данной работы.
Применяемые в настоящее время регулируемые и следящие электроприводы (ЭП) построены, в основном, с применением принципов подчиненного регулирования координат. В качестве координат выступают ток якоря двигателя, его скорость вращения и угол поворота вала двигателя (перемещение исполнительного органа рабочей машины).
Для решения поставленных в разделе 1.5 задач нет необходимости приводить полное точное математическое описание данной электромеханической системы. Так как нашей целью является не описание процессов, протекающих внутри этой системы, а регулирование поведения данной системы в целом. К тому же, как было видно из описанного выше, современные электромеханические системы имеют сложную структуру и их описание будет громоздким, что не дает возможности применения этого описания в однокристальных ЭВМ, на которые ориентируется данный разрабатываемый метод.
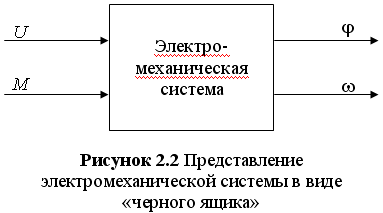
В связи с этим предлагается рассматривать данную электромеханическую систему как один неразделимый блок, не останавливаясь на конкретных процессах и взаимосвязях имеющих место быть, т.е. рассматривать данную систему как, так называемый, «черный ящик». На рисунке 2.2 приведена условное изображение этой системы в виде «черного ящика». Известно, что выходными координатами системы являются угол j и скорость w поворота исполнительного органа рабочей машины (вала двигателя). Входной координатой является момент М, характеризующий тормозящий момент на валу двигателя, развиваемый рабочей установкой; момент сил трения в подшипниках, о воздух, на коллекторе электрической машины и в зубчатых передачах редуктора; тормозящий момент, вызываемый потерями на гистерезис и вихревые токи в сердечнике якоря. Управляющим параметром, в данном случае, является напряжение U на якоре электродвигателя.
Объекты и системы управления состоят из элементов, имеющих различную природу. Для анализа их взаимодействия удобно перейти к единообразному, стандартному описанию.
Так как разрабатываемый метод ориентируется на использование в однокристальных ЭВМ, то описание системы необходимо производить в дискретном виде. Для этого в описании динамической системы вместо дифференциальных уравнений предложено использовать уравнения в конечных разностях или разностные уравнения.
Для математического описания данной системы было предложено использовать разностное уравнение специального вида, которое носит название авторегрессионно-регрессионной модели объекта (АРРМ).
Общий вид авторегрессионно-регрессионной модели порядка (N, L) представлен ниже:
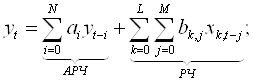 (2.1)
(2.1)
где АРЧ — авторегрессионная часть, РЧ — регрессионная часть; N и L — целые числа, определяющие порядок АРРМ (![]() ); N — порядок авторегрессионной, а L — порядок регрессионной части модели; ai и bi — параметры АРРМ. Вектор параметров определяется на этапе идентификации модели.
); N — порядок авторегрессионной, а L — порядок регрессионной части модели; ai и bi — параметры АРРМ. Вектор параметров определяется на этапе идентификации модели.
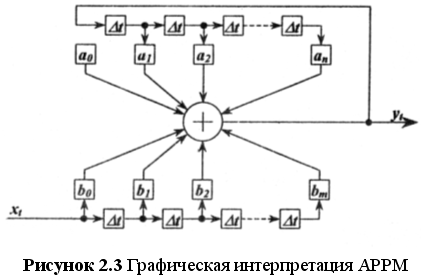
Авторегрессионная часть является выходом модели, а регрессионная часть — входом, т.е. yt является выходным процессом, а xt — входным. В частном случае, когда N = 0, модель не имеет входа и называется авторегрессионной моделью, если L = 0, то будет получена регрессионная модель. Графическая интерпретация АРРМ приведена на рисунке 2.3. В отличие от дифференциальных уравнений, авторегрессионно-регрессионные модели могут описывать как непрерывные, так и дискретные по своей природе объекты.
В нашем случае входными процессами являются момент М и напряжение на якоре двигателя U, которое также является управляющим воздействием. Выходным параметром является угол поворота оси антенны. Таким образом вид авторегрессионно-регрессионной модели в нашем случае будет иметь вид:
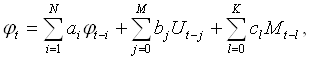 (2.2)
(2.2)
или если принять в качестве выходного параметра скорость w поворота вала, то выражение (2.2) примет вид:
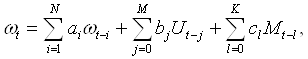 (2.3)
(2.3)
где ![]() — параметры модели, (N, M+K) — порядок модели.
— параметры модели, (N, M+K) — порядок модели.
В режиме холостого хода выражения (2.2) и (2.3) будут иметь вид:
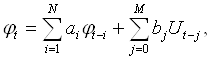 (2.4)
(2.4)
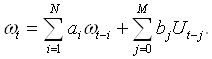 (2.5)
(2.5)
Параметры этих моделей не имеют прямого физического смысла и зависят от выбора шага квантования по времени. Порядок модели как и ее параметры находятся в процессе идентификации.
По своему физическому смыслу модели (2.3) и (2.5) являются устойчивыми, а (2.2) и (2.4) — неустойчивыми. Модели (2.2) и (2.4) являются неустойчивыми, так как выходная координата (угол поворота) постоянно увеличивается при постоянном входном воздействии (напряжении на якоре), а скорость вращения стремится к некоторому определенному значению.
Авторегрессионно-регрессионная модель является устойчивой, если устойчивой является соответствующая ей авторегрессионная модель. Выполнить анализ устойчивости можно после идентификации параметров модели.
2.2 Идентификация авторегрессионно-регрессионной моделиИдентификация динамической системы заключается в отыскании математических моделей, поведение которых подобно поведению самой системы (объекта). Модель объекта необходима для синтеза законов управления, так как управление определяется в результате анализа прогноза поведения объекта.
При использовании в качестве модели объекта АРРМ предполагается, что объект является линейным (хотя бы для рассматриваемых режимов работы) или допускает линейное описание. Реальные же объекты являются нелинейными.
Для идентификации необходимо выбрать порядок модели (ее вид), а затем идентифицировать ее параметры (коэффициенты). Вид модели определяется экспериментально, из заданного списка возможных моделей. Для каждой из них идентифицируются параметры, и оценивается ее точность. На основании анализа точности описания и сложности модели делается вывод о ее пригодности. Таким образом, в общем случае, процесс выбора модели и идентификации параметров является циклическим процессом.
Для описания данной электромеханической системы будем использовать АРРМ, имеющую вид (2.2).
На начальном этапе необходимо выбрать порядок авторегрессионно-регрессионной модели. Для достижения этой цели проводился эксперимент, в котором циклически проводился подбор порядка модели с определением точности полученной на каждом шаге модели, исходя из реальных экспериментально полученных данных. Поиск подходящего порядка модели проводился в диапазоне p = 0..20.
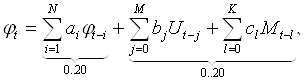
В результате была найдена модель, удовлетворяющая требованиям точности, порядок которой составляет (3, 3). Общий вид АРРМ объекта (электромеханической системы) представлен ниже:
![]() (2.6)
(2.6)
Если за основу взять выражение (2.3), то конечная АРРМ будет иметь вид:
![]() (2.7)
(2.7)
В режиме холостого хода, когда момент М на валу двигателя равен нулю (т.е. ![]() ), выражения (2.6) и (2.7) примут вид:
), выражения (2.6) и (2.7) примут вид:
![]() (2.8)
(2.8)
![]() (2.9)
(2.9)
Однако перед окончательным выбором вида математической модели, следует упомянуть следующий факт: особенностью рассматриваемой системы является то, что тормозящий момент на валу электропривода имеет константный характер так как обусловлен, как говорилось в разделе 2.1, силами трения, а также, так называемой, ветровой нагрузкой, которая симметрично действует и на разгон и на торможение. Таким образом тормозящий момент существует и равен некоторому константному значению, а следовательно он будет учитываться при идентификации системы автоматически.
Таким образом, первый этап идентификации, на котором был определен порядок модели, выполнен. Далее будут использоваться выражения (2.8) и (2.9).
Вторым этапом идентификации является нахождение численных значений параметров авторегрессионно-регрессионной модели: ![]() , которые по своему смыслу являются весовыми коэффициентами.
, которые по своему смыслу являются весовыми коэффициентами.
Нахождение численных значений параметров модели будем производить с помощью метода наименьших квадратов (МНК). В результате применения метода МНК будет получен вектор оценочных значений параметров модели. Суть МНК заключается в минимизации суммы квадратов ошибок исходных уравнений (2.8) для данного набора фазовых координат динамической системы.
Для идентификации параметров необходимо наблюдать входные и выходные фазовые координаты системы. Для нашей системы, как упоминалось выше, входной координатой является Ut, выходной координатой — jt. Данные наблюдений заносятся в таблицу (таблица 2.1):
Таблица 2.1 Исходные данные для идентификации
|
| |||||
| t | jt | jt-1 | jt-2 | jt-3 | Ut |
| 1 | j0 | — | — | — | U0 |
| 2 | j1 | j0 | — | — | U1 |
| 3 | j2 | j1 | j0 | — | U2 |
| 4 | j3 | j2 | j1 | j0 | U3 |
| 5 | j4 | j3 | j2 | j1 | U4 |
| … | … | … | … | … | … |
| t | jt | jt–1 | jt–2 | jt–3 | Ut |
Далее из таблицы 2.1 формируются матрицы X и Y, которые имеют вид:


Конечной расчетной формулой МНК является выражение (2.10):
![]() (2.10)
(2.10)
где ![]() — вектор-столбец оценочных параметров модели (2.8), X и Y — указанные выше матрицы.
— вектор-столбец оценочных параметров модели (2.8), X и Y — указанные выше матрицы.
Таким образом, в результате вычислений получается вектор-столбец оценочных параметров модели (2.8) имеющий вид:
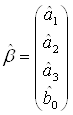 (2.11)
(2.11)
Или
![]()
Для идентификации модели электромеханической системы использовались данные, экспериментально полученные при проведении исследований динамических характеристик и параметров привода РЛС в ООО НПО «Горизонт» [3]. Значения для каждой фазовой координаты представляют собой векторы, полученные путем измерения данной координаты в конкретные промежутки времени, определяемые временем квантования, которое составило ![]() секунды.
секунды.
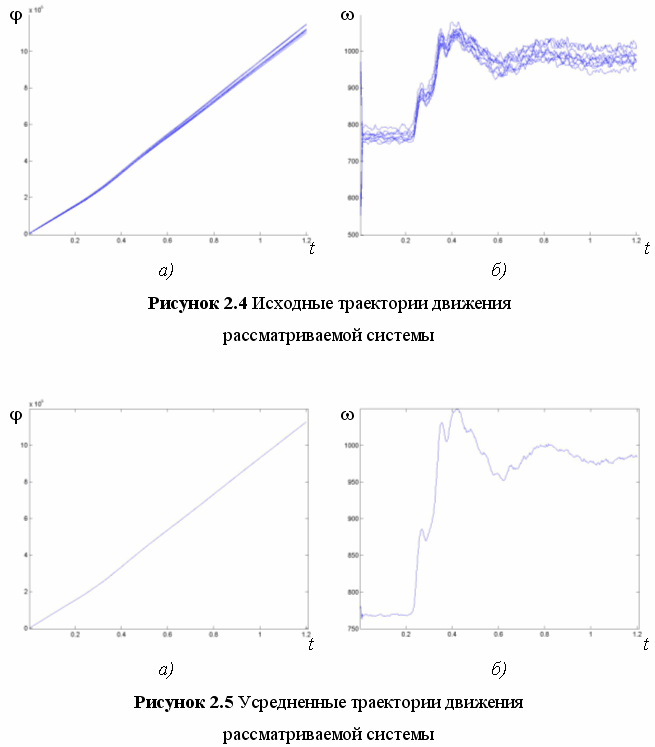
В качестве исходных данных выступают скорость поворота исполняемого органа привода и управляющее воздействие. В процессе проведения эксперимента были получены несколько траекторий движения системы, а именно девять, после чего было проведено усреднение результатов. Так как измерения проводились с малым временем квантования, то для уменьшения громоздкости расчетов была проведена интерполяция исходных данных с временем квантования ![]() секунды. Экспериментальные данные представлены на рисунках 2.4 — 2.7 и представляют собой зависимость значений фазовых координат от времени.
секунды. Экспериментальные данные представлены на рисунках 2.4 — 2.7 и представляют собой зависимость значений фазовых координат от времени.
На рисунке 2.4 представлены множество траекторий, снятых с экспериментальной установки в процессе эксперимента. На рисунке 2.5 представлены усредненные траектории, а на рисунке 2.6. — интерполированные; рисунки а) представляют собой угол поворота, а рисунки б) — скорость. На рисунке 2.7 изображено подаваемое в процессе эксперимента управление.
Используя приведенные исходные данные, была построена таблица, как было показано выше и с помощью нее сформированы матрицы X и Y. Подставив эти матрицы в выражение (2.10), был получен вектор-столбец оценочных параметров авторегрессионно-регрессионной модели объекта. Значения параметров АРРМ имеют вид, приведенный ниже:
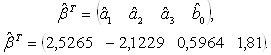 (2.12)
(2.12)
Таким образом был получен общий вид авторегрессионно-регрессионной модели объекта, который приведен ниже:
![]() (2.13)
(2.13)
Для получения значений wt, необходимо задаться выражением:
![]()
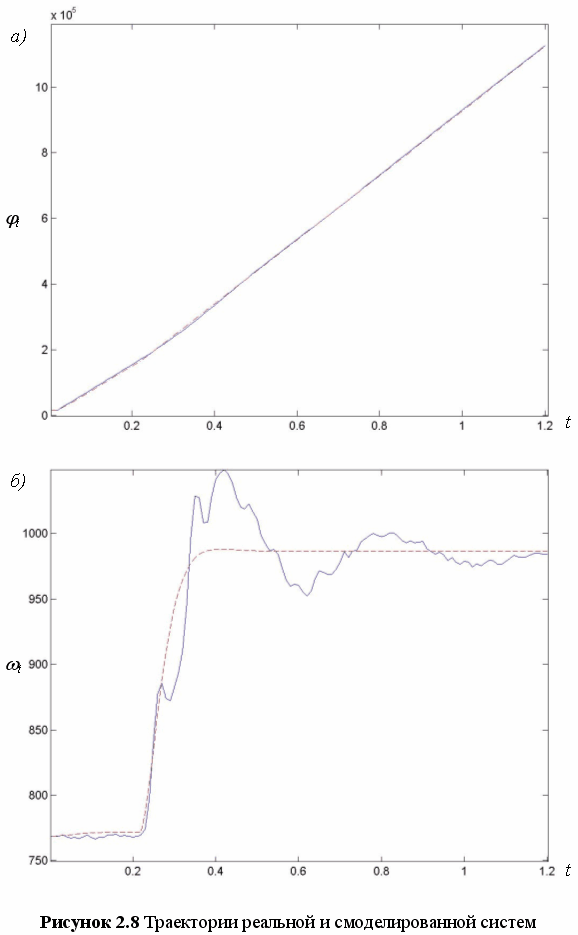
Проверим адекватность полученной модели. Для этого сравним исходные данные, полученные экспериментально, и данные полученные с помощью математической модели, вид которой приведен выше.
На рисунке 2.8 представлены эталонная и смоделированная траектории движения системы. На рисунке 2.8, а изображены графики изменения угла поворота jt, а на рисунке 2.8, б — графики изменения скорости поворота wt. Из графика видно, что авторегрессионно-регрессионная модель объекта, с данными параметрами адекватно описывает поведение реальной системы.
Таким образом был получен вид авторегрессионно-регрессионной модели, удовлетворяющий требованием точности. Процесс идентификации завершился за шаг.
Следует упомянуть тот факт, что данная модель описывает траектории системы не в принятых единицах измерения углов и скоростей, а в некоторых унифицированных импульсах, которые используются в данной электромеханической системе. Для перехода к градусам необходимо воспользоваться следующим выражением: ![]() где j — искомый угол, n — количество импульсов.
где j — искомый угол, n — количество импульсов.
Любая реальная техническая система имеет ограничения на управление. Это обусловлено конструкцией и техническими характеристиками рассматриваемой системы. Ограничения отражаются в технических условиях на эксплуатацию системы.
Управляющим параметром электропривода является напряжение на якоре, которое обозначается U. В связи с техническими особенностями данного объекта управления, напряжение на якоре не может превышать некоторого предельно допустимого значения. Это обусловлено максимальным током в обмотке якоря ![]() , а также характеристиками источника энергии, используемого в данной системе. Таким образом, необходимо учитывать это ограничение при разработке управляющего устройства.
, а также характеристиками источника энергии, используемого в данной системе. Таким образом, необходимо учитывать это ограничение при разработке управляющего устройства.
Еще одним ограничением на управляющий параметр, является то, что величина не может меняться скачкообразно на сколь угодно большую величину. Это ограничение обусловлено возможностями и конструкцией источника энергии и регулирующего устройства, которое задает характер изменения величины управляющего параметра. Это второе ограничение, накладываемое на управление.
Таким образом в данной работе рассматривается следующий случай: область управления U имеет размерность 2, т.е. эта область представляет собой плоскость в пространстве управлений.
Математически область управления U для данной системы задается следующей системой выражений:
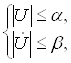 (2.14)
(2.14)
где первое выражение накладывает ограничение на величину, а второе — на скорость изменения значения управляющего параметра. Выражение (2.14) представляет собой ограничения, написанные для непрерывных систем. Так как в рассматриваемом случае рассматривается дискретное время, то перепишем систему (2.14) в виде, пригодном для дискретных систем:
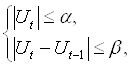 (2.15)
(2.15)
где ![]() — представляет собой разность значений управляющего параметра текущего и предыдущего моментов времени, что для дискретных систем является аналогом скорости непрерывных систем.
— представляет собой разность значений управляющего параметра текущего и предыдущего моментов времени, что для дискретных систем является аналогом скорости непрерывных систем.
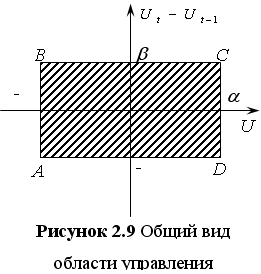
На рисунке 2.9 представлен общий вид области управления для рассматриваемой задачи.
Реальные численные значения данных границ зависят от коэффициентов масштабирования реальной системы, которые определяются входящими в систему усилителями и преобразователями, и выбираются для каждого моделируемого объекта индивидуально, в строгом соответствии с техническими условиями и правилами эксплуатации. Для данной системы ограничения имеют вид:
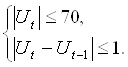 (2.16)
(2.16)
Для того чтобы перейти из пространства управлений в базис времени необходимо воспользоваться теоремой Гамкрелидзе о числе переключений [1]. Движение будет осуществляться по граням области управления, т.е. по сторонам прямоугольника в пространстве управлений. На рисунке 2.10 представлены ограничения в координатах (t, U).
Ограничение на величину параметра представляет собой две горизонтальные линии, обозначенные на рисунке пунктиром, с ординатами a и –a. Ограничение на скорость изменения величины управляющего параметра определяется углом g наклона траектории:
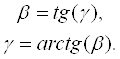
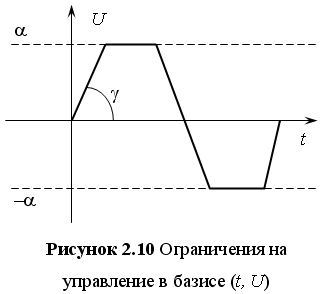
Как видно из рисунка 2.10 управление имеет вид кусочно-гладкой функции с несколькими переключениями.
Точки переключений в базисе (t, U), соответствуют вершинам прямоугольника области управления (рисунок 2.9). Участок 1 на рисунке 2.11 соответствует движению по часовой стрелке по отрезку BC. Это движение будет длиться до момента достижения точки C, далее движение будет происходить по отрезку CD, на рисунке 2.11 этому движению соответствует участок 2. Движение по участку CD в пространстве управлений будет длиться до момента достижения точки D и т.д.
Существует один интересный случай, когда скорость управления, скачком меняется на противоположное значение, т.е. в пространстве управлений будет наблюдаться скачок с отрезка BC на отрезок CD. Этому соответствует участок 2’ в базисе (t, U). Участок 2’’ на рисунке 2.11 соответствует скачку с отрезка BC на отрезок CD в пространстве управлений, не достигнув точки переключения.
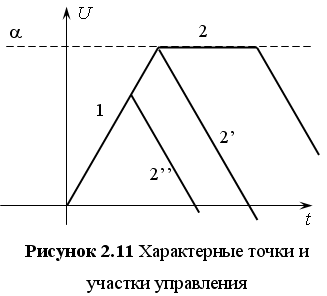
На самом деле такой характер изменения скорости допустим, так как при задании ограничений говорилось, что скачком не может меняться только величина управляющего параметра, тогда как на скорость изменения этого параметра такого ограничения не накладывалось. Это не противоречит рассуждениям приведенным в разделе 1.1. То есть управляющий параметр является не безынерционным, а скорость изменения этого параметра — безынерционным. Правомерность этого утверждения легко подтверждается физическим смыслом управления, являющегося напряжением на якоре.
Необходимо рассмотреть случай, при котором возникшую ошибку можно ликвидировать за один шаг. Запишем регулятор для АРРМ вида (2.8), обеспечивающий равенство ![]() . Выражение для такого регулятора имеет вид:
. Выражение для такого регулятора имеет вид:
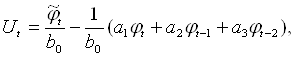
или для ошибки:
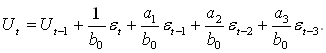 [5]
[5]
Будем называть такое управление одношаговым. Для реализации такого управления необходимо, чтобы выработанное таким образом управление также удовлетворяло условию (2.15), а иначе такое управление является нереализуемым за один шаг.
2.4 Формирование оптимальных траекторийКак было указано выше (раздел 1.1), оптимальной траекторией называют траекторию x(t), по которой фазовая точка за кратчайшее время переходит из состояния x0 в состояние x1. Такой переход будет осуществляться при приложении оптимального управления. Оптимальным управление будет при движении по граням (границам) области управления в пространстве управлений. Для данной задачи, областью управления является прямоугольник (рисунок 2.9). Таким образом, управления будут представлять собой константные и линейно-нарастающие воздействия.
Для построения оптимальных траекторий необходимо найти решение математического выражения, с помощью которого описывается объект управления. В данном случае это авторегрессионно-регрессионная модель. Есть несколько способов решения данного уравнения: численный и аналитический. Численное решение удобно для применения ЭВМ, но имеет один недостаток. Так как решение имеет итерационный характер, то в процессе вычислений с каждым шагом накапливается ошибка. Аналитическое решение не страдает указанным недостатком и является более универсальным и точным по сравнению с численным, но в данном случае проблемы сопряжены с поиском решения.
Из теории линейных разностных уравнений известно, что общий вид аналитического решения для выражения (2.8) имеет вид:
![]() (2.17)
(2.17)
где ![]() — общее решение линейного неоднородного разностного уравнения,
— общее решение линейного неоднородного разностного уравнения, ![]() — общее решение линейного однородного разностного уравнения,
— общее решение линейного однородного разностного уравнения, ![]() — частное решение линейного неоднородного разностного уравнения. Более подробно выражение (2.17) можно записать в виде:
— частное решение линейного неоднородного разностного уравнения. Более подробно выражение (2.17) можно записать в виде:
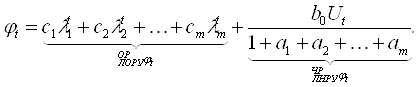 (2.18)
(2.18)
где m — порядок авторегрессии; ![]() — константы, определяемые из начальных условий;
— константы, определяемые из начальных условий; ![]() — корни характеристического уравнения (2.19) для исходного разностного уравнения (2.8),
— корни характеристического уравнения (2.19) для исходного разностного уравнения (2.8), ![]() — коэффициенты авторегрессионно-регрессионной модели (2.8). [6]
— коэффициенты авторегрессионно-регрессионной модели (2.8). [6]
![]() (2.19)
(2.19)
где m — порядок авторегрессии. Для третьего порядка авторегрессии, выражение (2.18) будет иметь вид:
![]() (2.20)
(2.20)
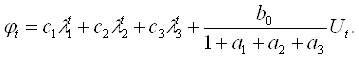 (2.21)
(2.21)
Подставим в выражения (2.20) и (2.21) коэффициенты модели (2.13). После подстановки выражения будут иметь вид:
![]() (2.22)
(2.22)
![]()
Для нахождения общего вида аналитического решения уравнения (2.13) необходимо найти корни характеристического уравнения (2.22) и коэффициенты ci выражения (2.21).
При нахождении корней характеристического уравнения (2.22) удобно воспользоваться функцией roots математического пакета MatLab. В результате расчетов были получены следующие значения:
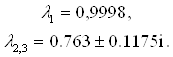
Так как в результате вычислений был получен комплексно-сопряженный корень, то данное аналитическое решение является не удобным для использования в алгоритме и далее вычисления будут проводиться численными методами. Ниже приведены построенные оптимальные траектории в пространстве управлений. Эти траектории построены с учетом ограничений налагаемых на управление. Ограничения имеют вид системы (2.16). Таким образом, были построены траектории, соответствующие константному значению управляющего параметра и линейно-нарастающему.
На рисунке 2.12 представлены траектории системы соответствующие константному значению управляющего параметра без учета ограничения на скорость. На графике 2.12, а представлен график управления, на графике 2.12, б — траектория системы в пространстве фазовых координат системы (jt, wt), на графике 2.12, в — траектория системы в базисе (t, jt), на графике 2.12, г — траектория системы в базисе (t, wt).
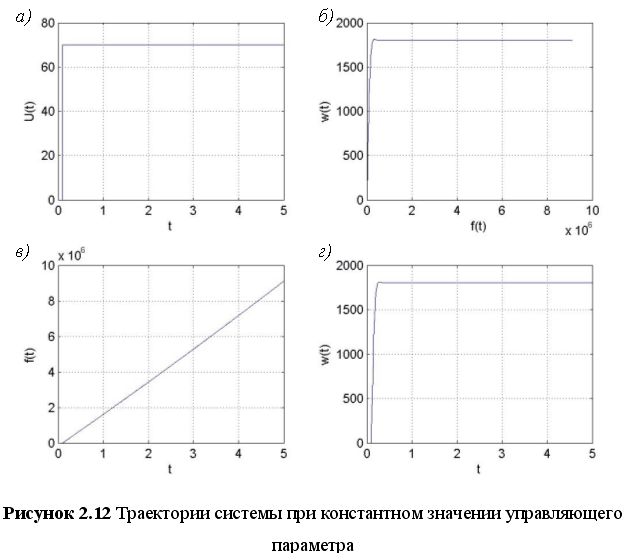
На рисунке 2.13 представлены траектории системы соответствующие линейно-нарастающему значению управляющего параметра без учета ограничения на значение параметра. На графике 2.13, а представлен график управления, на графике 2.13, б — траектория системы в пространстве фазовых координат системы (jt, wt), на графике 2.13, в — траектория системы в базисе (t, jt), на графике 2.13, г — траектория системы в базисе (t, wt).
В процессе работы системы, управляющий параметр будет иметь несколько моментов переключения. В качестве иллюстрации этого случая приведен рисунок 2.14.
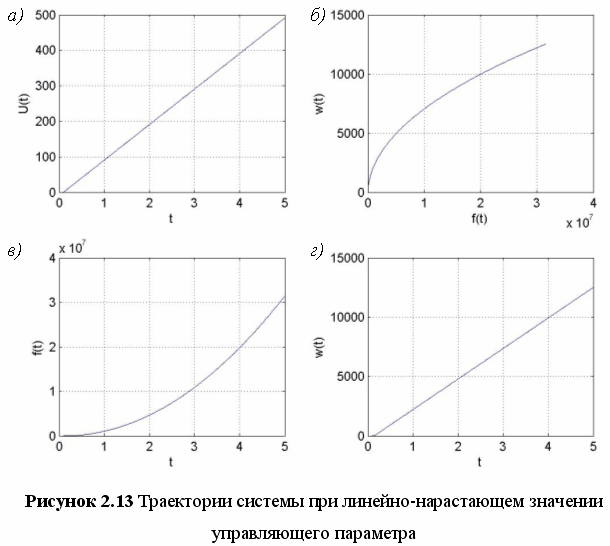
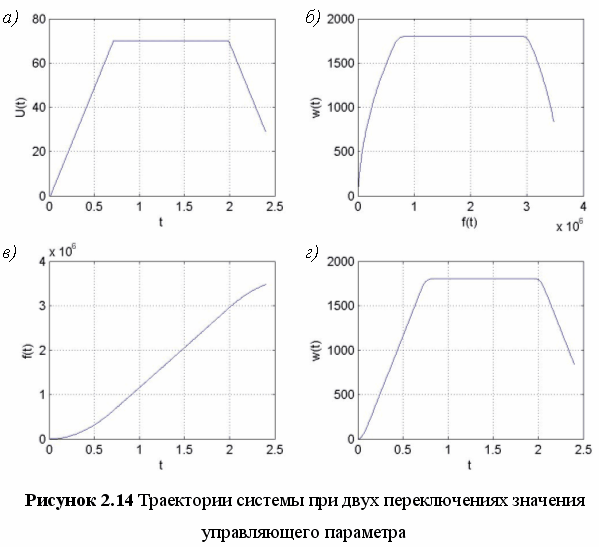
Движение системы при оптимальном управлении определяется начальными условиями. Рассмотрим начальные условия в базисе (t, jt). Для данной системы максимальный угол рассогласования не может превышать 180°, по модулю. Таким образом, в базисе (t, jt) необходимо выделить ограничения –p, +p, которые представляют собой горизонтальную полосу, внутри которой и будут располагаться точка, соответствующая начальному значению фазовой координаты j. На рисунке 2.15, показаны несколько вариантов начальных условий.
В зависимости от начальных условий, в базисе (jt, wt) будет существовать множество траекторий. При различных углах в начальных условиях, траектории будут располагаться по горизонтали.
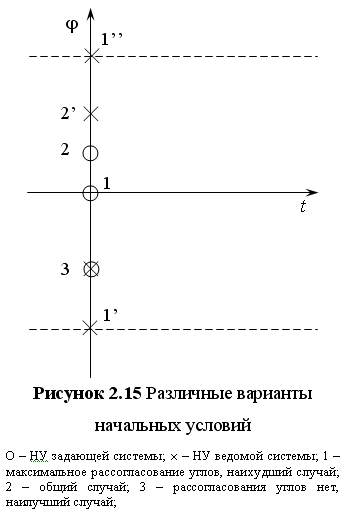
Как говорилось при постановке задачи, данная проблема решается в базисе ошибок. Для перехода в базис ошибок необходимо воспользоваться выражением (1.13):
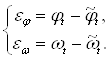
Это выражение переводит множество траекторий из базиса (jt, wt), в базис ошибок.
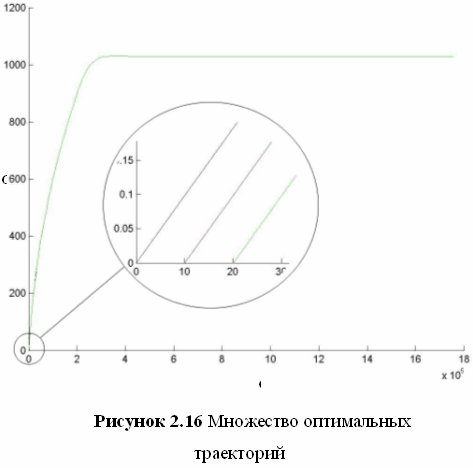
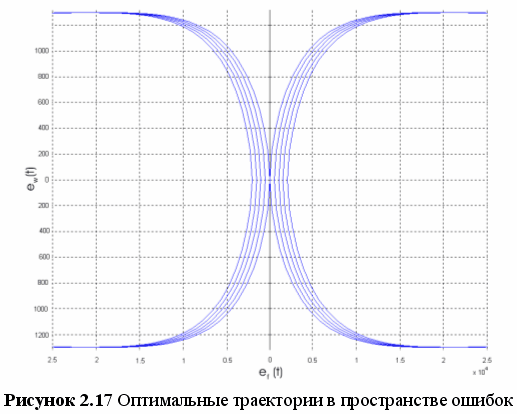
На рисунке 2.16 изображено множество оптимальных траекторий в базисе (jt, wt), а на рисунке 2.17 изображены те же траектории в базисе ошибок. Положение траекторий в базисе ошибок зависит от начальной ошибки по обеим фазовым координатам, то есть от угла рассогласования и разности скоростей.
При различных начальных углах оптимальные траектории будут распределяться по горизонтали. На рисунке 2.16 показаны три траектории с начальными углами 0°, 10° и 20°. В указанных случаях, начальная скорость равна нулю.
При различных начальных скоростях, траектории будут иметь идентичный вид, но начальной точкой движения будет точка не лежащая на оси абсцисс.
Для последующего анализа решений в базисе ошибок, необходимо рассмотреть несколько вариантов начальных условий. Для этого необходимо разбить пространство ошибок на характерные подпространства.
Так как угол рассогласования не может превышать угла в 180°, то и ошибка не может превышать этого значения. Таким образом, в базисе ошибок можно выделить вертикальную полосу шириной 2p ([–p, +p]), за границы которой ошибка по углу не может выходить. На самом деле, если ошибка ![]() превышает значение p, то угол рассогласования рассчитывается как показано ниже:
превышает значение p, то угол рассогласования рассчитывается как показано ниже:
![]() (2.23)
(2.23)
где ![]() — новое значение ошибки, не превышающее p.
— новое значение ошибки, не превышающее p.
Следует также упомянуть следующее: при положительной ошибке ![]() начальная точка будет находиться справа от оси ординат, а при положительной ошибке
начальная точка будет находиться справа от оси ординат, а при положительной ошибке ![]() — выше оси абсцисс.
— выше оси абсцисс.
Так как управление имеет ограничение на величину, то величина скорости вращения вала системы не будет превышать некоторого максимального установившегося значения. Таким образом, величина ошибки ![]() тоже не будет превышать некоторого максимального значения, определяемого максимальной скоростью системы и равной
тоже не будет превышать некоторого максимального значения, определяемого максимальной скоростью системы и равной ![]() . Из этого следует, что в базисе ошибок необходимо выделить горизонтальную полосу шириной
. Из этого следует, что в базисе ошибок необходимо выделить горизонтальную полосу шириной ![]() (
(![]() ), за границы которой ошибка по скорости не может выходить.
), за границы которой ошибка по скорости не может выходить.
Таким образом, в пространстве ошибок выделена прямоугольная область допустимых значений ошибок. Все движения будут происходить именно в этой области.
На рисунке 2.17 показаны оптимальные траектории в пространстве ошибок. Выделим из всего множества траекторий две, приводящие в ноль. Будем называть эти траектории главными. У левой главной траектории выделим верхнюю ветвь, а у правой — нижнюю. Движение по этим ветвям приводит в начало координат. Так как в разделе 1.4 была поставлена задача (1.12), то эти две ветви необходимо выделить особо, так как при движении по ним выполняется первое условие задачи (1.12).
Указанные выше ветви главных траекторий делят область ошибок на два подпространства P и Q. Анализ этих подпространств делается ниже.

Вокруг начала координат ограничим некоторую область S. Данная область соответствует такому положению системы, при котором управление необходимое для коррекции этой ошибки не будет превышать своего максимального значения, то есть не будет нарушаться первое выражение системы (1.13). В графической интерпретации, в пространстве управлений движение будет происходить по горизонтальным границам (рисунок 2.7). Верхняя и нижняя ветки главных траекторий разбивают пространство S на два подпространства — S1 и S2.
Таким образом, были построены четыре подпространства в пространстве ошибок, которые изображены на рисунке 2.18.
Количество точек переключения и вид управления зависит от начальных условий. Рассмотрим различные варианты начальных условий:
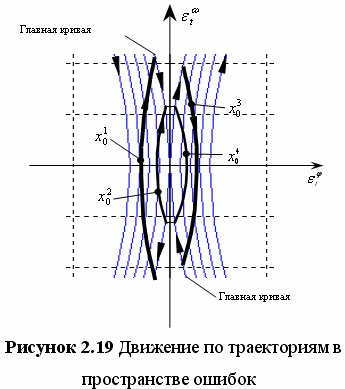
1) система находится в точке лежащей в плоскости P (точка ![]() на рисунке 2.19); в этом случае движение в пространстве ошибок будет проходить по траектории, состоящей из двух кривых, то есть траектория будет иметь два интервала постоянства; этому движению соответствует управление с тремя точками переключения (рисунок 2.20, участок 1);
на рисунке 2.19); в этом случае движение в пространстве ошибок будет проходить по траектории, состоящей из двух кривых, то есть траектория будет иметь два интервала постоянства; этому движению соответствует управление с тремя точками переключения (рисунок 2.20, участок 1);
2) система находится в точке лежащей в плоскости S1 (точка ![]() на рисунке 2.19); в этом случае движение в пространстве ошибок будет проходить также по двум кривым, то есть траектория будет иметь два интервала постоянства; но этому движению соответствует управление с двумя точками переключения (рисунок 2.20, участок 2);
на рисунке 2.19); в этом случае движение в пространстве ошибок будет проходить также по двум кривым, то есть траектория будет иметь два интервала постоянства; но этому движению соответствует управление с двумя точками переключения (рисунок 2.20, участок 2);

3) в случае когда система находится в подпространстве Q, движение будет иметь такое же количество интервалов постоянства и точек переключения как и случай 1, но знак управляющего параметра изменится на противоположный (рисунок 2.19, точка ![]() , рисунок 2.20, участок 3);
, рисунок 2.20, участок 3);
4) в случае когда система находится в подпространстве S2, движение будет иметь такое же количество интервалов постоянства и точек переключения как и случай 2, но знак управляющего параметра изменится на противоположный (рисунок 2.19, точка ![]() , рисунок 2.20, участок 4);
, рисунок 2.20, участок 4);
Т. о. данные траектории являются решением задачи об оптимальном быстродействии и задача сводится к нахождению моментов времени переключений управляющего параметра U.
При определении моментов точек переключения можно использовать как аналитические выражения, так и численные методы. При определении моментов точек переключения аналитически необходимо решить систему уравнений вида (2.18) для частного случая, где одно из уравнений написано для кривой, являющейся главной траекторией, а другое — для кривой, проходящей через точку, в которой находится система в данный момент и пересекающую главную траекторию, описанную первым уравнением системы. Общий вид системы приведен ниже:
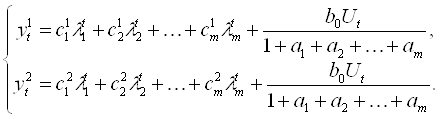
В том случае, если аналитические выражения не удовлетворяют требованиям, предъявленным к алгоритму в разделе 1.3, точки переключения необходимо искать численными методами.
Как уже было сказано выше, численные методы имеют итерационный характер, и не обладают высокой точностью.
2.6 Общая структура системы оптимального управленияВ соответствии с выше изложенным материалом, построена система оптимального управления. Система представляет собой устройство, корректирующее управление на каждом шаге. Под шагом понимается момент времени, в который производится измерение угла как ведомого так и ведущего приводов.
Общая структура системы приведена на рисунке 2.21. В общей структурной схеме выделено два основных блока:
1) 1 — блок оптимального управления;
2) 2 — математическая модель объекта управления в виде АРРМ.
В блоке оптимального управления происходит выработка управления на каждом шаге.
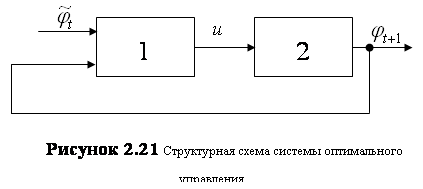
Рассмотрим блок оптимального управления (блок 1) подробнее. Развернутая структурная схема блока оптимального управления представлена на рисунке 2.22.
В структурной схеме на рисунке 2.22 выделены следующие блоки:
1) 1 — первый блок выбора алгоритма расчета управления;
2) 2 — второй блок выбора алгоритма расчета управления;
3) 3 — выдача управления последнего шага;
4) 4 — выдача одношагового управления;
5) 5 — расчет и выдача оптимального управления.
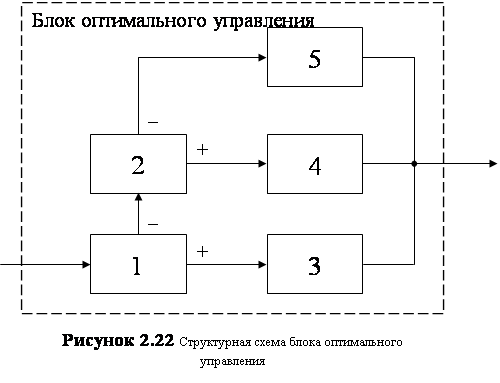
В блоке 1 происходит определение того, нужно ли корректировать значение управляющего параметра, то есть если ошибка не превышает некоторого предельно допустимого значения, то корректировка управляющего параметра не производится. В работу включается блок 3, который выдает управление последнего шага, которое обеспечило движение с допустимой ошибкой.
Если ошибка превышает предельно допустимое значение, то в блоке 2 выясняется, можно ли достигнуть предельно допустимого значения ошибки за один шаг. Если это возможно, то в работу вступает блок 4, в котором рассчитывается и выдается одношаговое управление.
Если за один шаг значение ошибки не удается свести к предельно допустимому, то в работу вступает блок 5, в котором делается прогноз на применяемое управление. В нем определяется знак управления, находится количество точек переключений значения управляющего параметра, рассчитываются моменты времени, в которые будет происходить переключение управляющего параметра и выдается управление на следующий шаг. Структура блока 5 (рисунок 2.22) приведена на рисунке 2.23.
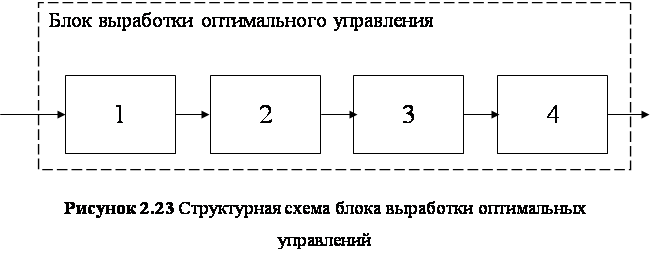
В структурной схеме на рисунке 2.23 выделены следующие блоки:
1) 1 — блок определения области в пространстве ошибок, в которой находится система на данном шаге;
2) 2 — блок определения знака управления и количества точек переключения управляющего параметра;
3) 3 — блок вычисления моментов времени, в которые будут происходить переключения управляющего параметра;
4) 4 — блок выработки управления на следующий шаг.
Таким образом, в данном разделе была рассмотрена общая структура блока оптимального управления, на основе которой можно построить его математическую модель.
2.7 Полученные результатыВ соответствии с проведенными рассуждениями и опираясь на структурную схему, приведенную в предыдущем разделе, была построена математическая модель данной системы оптимального управления. Математическое описание и программирование алгоритма проводилось в среде пакета MatLab 6.5.
Начальными данными для проведения расчетов является семейство траекторий системы, экспериментально полученные при проведении исследований динамических характеристик и параметров привода РЛС в ООО НПО «Горизонт» [3]. Исходные данные приведены на рисунке 2.4.
Для сравнения результатов были использованы данные, полученные в результате измерения выходных координат системы регулирования привода антенны, построенной с использованием ПИД-регулятора [3]. На рисунке 2.24 приведены зависимости ошибки рассогласования антенн (сплошная линия) и управления (пунктирная линия) от времени.

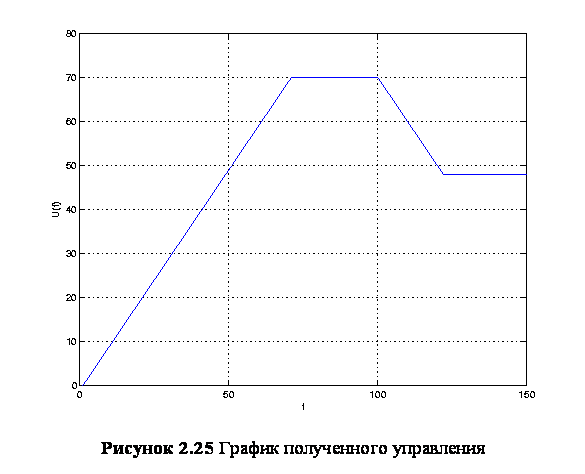
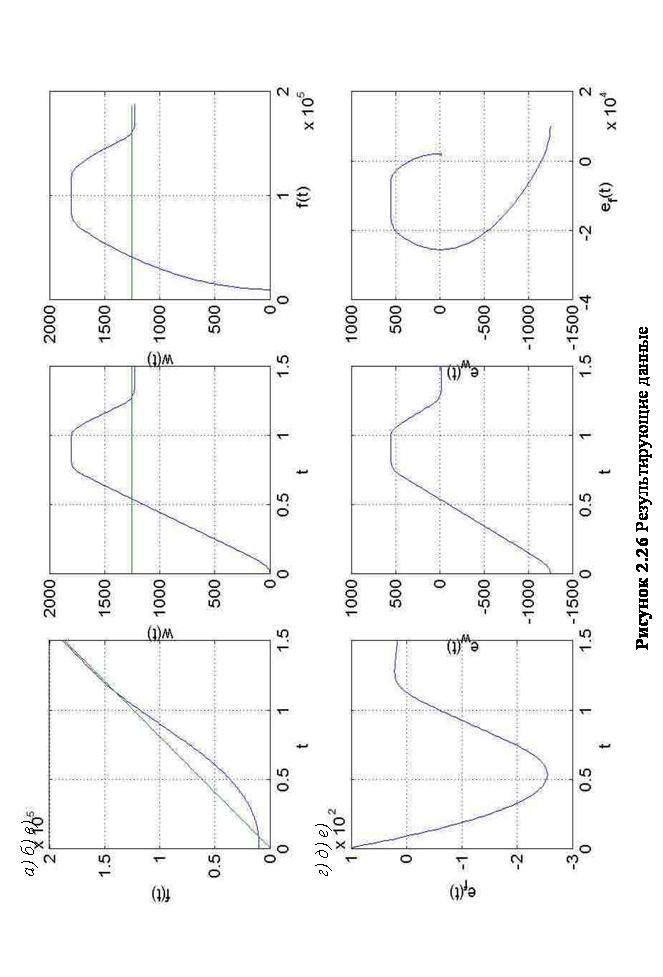
На рисунке 2.25 – 2.26 приведены данные, полученные в результате работы описанного выше алгоритма оптимального управления. На рисунке 2.25 приведен график зависимости полученного управления от времени. На рисунке 2.26, а приведен график зависимости угла поворота исполнительного органа установки от времени; на рисунке 2.26, б — график зависимости скорости поворота от времени; на рисунке 2.26, в — траектория движения системы в пространстве фазовых координат системы; на рисунке 2.26, г — график зависимости ошибки по углу поворота от времени; на рисунке 2.26, д — график зависимости ошибки по скорости поворота от времени и на рисунке 2.26, е — траектория движения системы в пространстве ошибок.
Проведем сравнительную характеристику представленных диаграмм. Из рисунка 2.24 видно, что процесс синхронизации антенн и выход на рабочий режим завершается приблизительно за десять секунд. Из графиков, приведенных рисунках 2.25 – 2.26 можно сделать вывод, что построенная система выходит на рабочий режим, приблизительно, за 1,5 секунды, что, почти, в 6 раз быстрее системы, построенной на основе ПИД-регулятора.
Процесс выхода на рабочий режим завершился с некоторой незначительной ошибкой, которую можно ликвидировать в следующем цикле работы системы оптимального управления. Этот процесс может продолжаться длительное время, поэтому необходимо задавать некоторое предельно допустимое значение ошибки, при котором работа системы будет удовлетворять техническим требованиям, предъявляемым к данной установке.
Таким образом, была смоделирована система управления, обеспечивающая более чем пятикратный выигрыш в быстродействии по сравнению с существующими системами, построенными на основе ПИД-регуляторов.
3 Практическая реализация 3.1 Реализация оптимального управления в среде пакета matlab
Для наглядного представления полученных в процессе работы алгоритма данных, все расчеты были выполнены в среде пакета MatLab. Была написана файл-функция Optimum_contr моделирующая работу блока оптимального управления и поведения системы в целом.
Структура программы имеет вид файл-функции, с несколькими подфункциями, описанными внутри данного файла. Такая организация позволяет запускать данную программу из командной строки интерпритатора MatLab.
Как было сказано выше, данная программа имеет ряд подпрограмм, описанных в основном файле.
Подпрограмма data_load() предназначена для загрузки начальных данных из файла.
Подпрограмма ident() производит вычисление параметров авторегрессионно-регрессионной модели с помощью метода МНК.
Для вычисления угловой скорости системы от угла существует подпрограмма calc_w(), которая вычисляет текущую скорость как разность текущего и предыдущего значений угла.
Подпрограмма upr() строит траекторию движения системы при заданном управлении в течении заданного количества шагов.
Подпрограмма u_calc() является основной частью системы. В ней производятся основные вычисления при выработке оптимального управления.
Подпрограмма znak() предназначена для определения начального знака управляющего параметра.
Подпрограмма countdot() определяет, в какую из областей пространства ошибок попадает фазовая точка системы в данный момент времени и вычисляет количество точек переключения управляющего параметра.
В подпрограмме dot_time() происходит вычисление моментов времени, в которые необходимо произвести переключение управляющего параметра.
В основном файле программы описаны и другие функции, рассматривать которые в рамках данной работы не имеет смысла, так как они являются вспомогательными и выполняют действия, необходимые для нормального функционирования системы.
3.2 Выбор микроконтроллераВыбор типа контроллера обуславливается несколькими факторами, а именно: производительностью арифметическо-логического устройства, ёмкостью оперативного запоминающего устройства и постоянного запоминающего устройства, доступностью ПО для создания программ и отладки, а также доступностью на российском рынке.
При создании алгоритма изначально учитывалась его адаптация к применению в микроконтроллерах. Таким образом, был получен алгоритм, основанный лишь на элементарных арифметических операциях, которые не требуют разработки дополнительных библиотек для производимых вычислений. При адаптации к конкретной системе, для данного алгоритма необходимо провести предварительные вычисления — идентификацию установки — для загрузки полученных параметров в микроконтроллер.
В настоящее время большое распространение получила продукция фирм: INTEL, MICROCHIP и ATMEL. Большинство микроконтроллеров MICROCHIP и ATMEL имеют FLASH память программ, что позволяет достаточно просто выполнять отладку программного обеспечения, а также его обновление. Микроконтроллеры ATMEL семейства АТ89 совместимы с семейством MCS-51, которое в настоящее время получило широкое распространение. Для MCS-51 разработаны и доступны библиотеки и системы создания программ и отладки. Среди микроконтроллеров ATMEL семейства АТ89 имеется контроллер AT89S8252, который допускает программирование непосредственно в оборудовании, в котором используется, что особенно удобно на этапе разработки и отладки.
Контроллер AT89S8252 работает с тактовой частотой 24 МГц, что обеспечивает производительность порядка двух миллионов операции в секунду, имеет встроенные операции умножения и деления, 8 Кбайт ПЗУ программ и 256 байт ОЗУ данных. Анализ основных характеристик контроллера AT89S8252 показывает его пригодность для решения задачи, поставленной в данной работе.
4 Экономическое обоснование проекта 4.1 Технико-экономическая характеристика
Данный проект является научно-исследовательской разработкой (НИР) в области автоматизации деятельности предприятий и относится к информационным системам автоматизированного проектирования.
Целью проекта является создание программного продукта (ПП), основанного на математическом пакете MatLab, реализующего математическую модель системы управления, построенной на основе оптимального закона, для системы слежения РЛС.
Данный проект можно отнести к научно-исследовательской работе, которая принадлежит к типу прикладных, направленных на решение научных проблем с целью получения конкретных результатов, которые могут быть использованы в опытно-конструкторских разработках (ОКР). Постановка данной задачи на разработку соответствует требованиям соответствующим данному виду НИР. Характер проведения разработки ПО был таков, что на ряду с основными задачами решалась масса проблем, заключающихся в поиске оптимальных решений использования тех средств, которые предоставляли доступные программное, аппаратное обеспечения и математическая база.
4.2 Маркетинговая ориентацияНа данном этапе разработки можно выбрать следующую маркетинговую ориентацию:
- преимущества у потребителя;
- с подкреплением;
- в реальном исполнении;
- по замыслу.
Ниже характеристики системы слежения РЛС с позиции маркетинга приведены в виде схемы на рисунке 4.1.
| Преимущества у потребителя: Система осуществляет автоматический вывод объекта (ДПТ) на заданную траекторию за минимальное время, а также слежение и отработку с необходимой точностью задающего (наблюдаемого) воздействия. | ||||||
| С подкреплением: Узкоспециализированный ПП, используемый для синтеза закона управления объектом (ДПТ), а также моделирования поведения системы под действием полученного оптимального закона управления. | ||||||
| В реальном исполнении: Структурная схема системы управления с набором аналитических выражений для основных управляющих органов объекта (ДПТ). | ||||||
| По замыслу: Автоматический выход на заданные параметры работы объекта за минимальное время. Движение по заданной траектории с установленной точностью. | ||||||
| Рисунок 4.1 Маркетинговая ориентация | ||||||
Пояснения к рисунку 4.1:
1) Основной целью создания ПП является автоматизация рабочего места научного сотрудника, а также поддержка принятия решений специалистов различного профиля. В ходе выполнения работы было проведено построение ММ информационной системы как задачи интеллектуальной системы автоматизированного проектирования и моделирования, были исследованы ее характеристики и вычислены некоторые параметры необходимые для практической реализации.
2) В реальном исполнении — это ПО информационной системы, функционально состоящее из структурной схемы системы управления с набором аналитических выражений для основных управляющих органов объекта (ДПТ). Система базируется на весьма распространенном в настоящее время классе ПЭВМ и имеет кросплатформенную реализацию.
3) Использование данного ПО носит специализированный характер: интерфейс пользователя обусловлен используемой программой интерпретатором (MatLab) и предназначен для освоения лицам, ранее работавшим с программой интерпретатором, но, возможно, не являющимися специалистами в области компьютерных технологий.
4) Основными достоинствами данного продукта являются гибкость, уникальность, оптимизация под требования конкретных задачи и заказчика. Система обладает относительно широкой аппаратной независимостью; некоторой программной (платформенной) независимостью (в пределах семейства Unix-подобных систем).
4.3 оценка научно-технической результативности и социальной эффективности НИРРезультатом НИР является достижение научного, научно-технического, экономического и социального эффекта.
Научный эффект характеризует получение новых научных знаний и отражает прирост информации, предназначенной для внутринаучного потребления. Научно-технический эффект характеризует возможность использования результатов выполняемых исследований в других НИР или ОКР и обеспечивает получение информации, необходимой для создания новой техники. Экономический эффект характеризуется выраженной в стоимостных показателях экономией живого и овеществленного труда в общественном производстве, полученной при использовании результатов прикладных НИР. Социальный эффект проявляется в улучшении условий труда, повышении экологических характеристик, развитии здравоохранения, культуры, науки, образования, и т.д.
Для итоговой оценки результатов НИР в зависимости от вида выполняемых исследований и поставленных целей в качестве критерия эффективности принимается один из видов эффекта, а остальные используются в качестве дополнительных характеристик.
Специфика проводимой работы не позволяет нам взять в качестве базового критерия — экономический или социальный эффект, поэтому имеет смысл остановиться на рассмотрении научного и научно-технического эффекта.
Количественную оценку научного эффекта целесообразно производить путем расчета научной результативности, научно-технического эффекта — научно-технической результативности.
Оценка научной и научно-технической результативности для НИР производится с помощью коэффициентов, рассчитываемых по формулам:
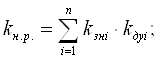 (4.1)
(4.1)
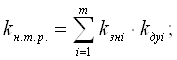 (4.2)
(4.2)
где ![]() — коэффициент научной результативности;
— коэффициент научной результативности; ![]() — коэффициент научно-технической результативности;
— коэффициент научно-технической результативности; ![]() — коэффициент значимости i-го фактора;
— коэффициент значимости i-го фактора; ![]() — коэффициент достигнутого уровня i-го фактора; n, m — соответственно количество факторов научной и научно-технической результативности.
— коэффициент достигнутого уровня i-го фактора; n, m — соответственно количество факторов научной и научно-технической результативности.
Для поисковых исследований рассчитывается коэффициент научной результативности и коэффициент научно-технической результативности.
При оценке научной и научно-технической результативности используются различные факторы, влияющие на их количественную оценку. В качестве факторов при оценке научной результативности могут быть приняты:
- новизна полученных или предполагаемых результатов;
- глубина научной проработки;
- степень вероятности успеха (при незавершенности работы).
В качестве факторов при оценке научно-технической результативности могут применяться:
- перспективность использования; масштаб реализации;
- завершенность полученных результатов.
В таблице 4.1 приведены факторы и признаки, характеризующую научную результативность, а в таблице 4.2 научно-техническую результативность НИР, а так же числовые значения ![]() и
и ![]() .
.
Таблица 4.1. Характеристика факторов и признаков научной результативности фундаментальных НИР
| Фактор научной результативности | Коэффициент значимости фактора, kнз | Качество фактора | Характеристика фактора | Коэффициент достигнутого уровня, kду | |
| Новизна полученных или предполагаемых результатов | 0,5 | Высокая | Получены принципиально новые результаты, неизвестные ранее науке, создана новая теория, открыта новая закономерность. | 1,0 | |
| Средняя | Установлены некоторые общие закономерности, методы, способы, позволяющие создать принципиально новые виды техники. | 0,7 | |||
| Недостаточная | Положительное решение поставленных задач на основе простых сообщений, анализ связей между фактами, распространение неизвестных научных принципов на новые объекты. | 0,3 | |||
| Тривиальная | Описание отдельных элементарных факторов, передача и распространение ранее полученных результатов, реферативные обзоры. | 0,1 | |||
| Фактор научной результативности | Коэффициент значимости фактора, kнз | Качество фактора | Характеристика фактора | Коэффициент достигнутого уровня, kду | |
| Глубина научной проработки | 0,35 | Высокая | Выполнены сложные теоретические расчеты, результаты проверены на большом количестве экспериментальных данных. | 1,0 | |
| Средняя | Сложность теоретических расчетов не высока, результаты проверены на ограниченном количестве экспериментальных данных. | 0,6 | |||
| Недостаточная | Теоретические расчеты просты, экспериментальная проверка не проводилась. | 0,1 | |||
| Степень вероятности успеха | 0,15 | Большая | Успех весьма возможен, имеется большая вероятность положительного решения поставленных задач. | 1,0 | |
| Умеренная | Поставленные задачи теоретически и технически осуществимы, успех возможен. | 0,6 | |||
| Малая | Теоретически осуществимо, но идея рискованная, успех весьма сомнителен. | 0,1 |
Таблица 4.2. Характеристика факторов и признаков научно-технической результативности фундаментальных НИР
| Фактор научной результативности | Коэффициент значимости фактора, kнз | Качество фактора | Характеристика фактора | Коэффициент достигнутого уровня, kду |
| Перспективность использования результатов | 0,5 | Первостепенная важность | Результаты могут быть использованы во многих научных направлениях, имеют значение для развития сопряженных наук. | 1,0 |
| Важная | Результаты будут использованы в конкретном научном направлении при разработке новых технических решений, направленных на существенное повышение производительности общественного труда в народном хозяйстве. | 0,8 | ||
| Полезная | Результаты будут использованы при проведении последующих НИР, при разработке новых технических решении в конкретной отрасли народного хозяйства. | 0,5 | ||
| Масштаб возможной реализации результатов | 0,3 | Народно-хозяйственный | Время реализации, лет: До 3 - 5 - 10 - свыше 10 | 0,5 0,6 0,8 1,0 |
| Отраслевой | Время реализации, лет: До 3 - 5 - 10 - свыше 10 | 0,8 0,7 0,5 0,3 | ||
| Отдельные организации и предприятия | Время реализации, лет: До 3 - 5 - 10 - свыше 10 | 0,2 0,3 0,4 0,5 | ||
| Завершенность полученных результатов | 0,2 | Высокая | Методика, инструкция, руководящие материалы, классификатор, нормативы. | 1,0 |
| Средняя | Технические задания на прикладные НИР или ОКР | 0,8 | ||
| Фактор научной результативности | Коэффициент значимости фактора, kнз | Качество фактора | Характеристика фактора | Коэффициент достигнутого уровня, kду |
| 0,2 | Достаточная | Рекомендации, развернутый анализ, предложения. | 0,6 | |
| Недостаточная | Обзор, информационным сборник. | 0,4 |
Произведем расчет данных коэффициентов:
1. Оценка научно-технической результативности:
1.1. Новизна полученных или предполагаемых результатов: ![]() . Качество фактора: средняя. Установлены некоторые общие закономерности, методы, способы, позволяющие создать принципиально новые виды техники
. Качество фактора: средняя. Установлены некоторые общие закономерности, методы, способы, позволяющие создать принципиально новые виды техники ![]() .
.
1.2. Глубина научной проработки: ![]() . Качество фактора: средняя. Сложность теоретических расчетов не высока, результаты проверены на ограниченном количестве экспериментальных данных
. Качество фактора: средняя. Сложность теоретических расчетов не высока, результаты проверены на ограниченном количестве экспериментальных данных ![]() .
.
1.3. Степень вероятности успеха: ![]() . Качество фактора: умеренная. Поставленные задачи теоретически и технически осуществимы, успех возможен
. Качество фактора: умеренная. Поставленные задачи теоретически и технически осуществимы, успех возможен ![]() .
.
Похожие работы
... информации. Набираемая информация отображается на дисплее, что позволяет контролировать ее правильность. Клавиатура и дисплей АИС должны быть независимыми от других навигационных устройств. Судовыми системами отображения АИС могут быть система отображения электронных карт (ECDIS, ECS, RCDS), РЛС, САРП или дисплей персонального компьютера. АИС и связанные с ней датчики информации питаются от ...
... , то необходимость в дополнительной линии передачи вообще отпадает при передаче энергии на сотни километров, поскольку вся излучаемая энергия может быть перехвачена приемным устройством с апертурой приемлемых размеров. В диапазоне субмиллиметровых волн отношение допустимых размеров апертур к длине волны заметно уменьшается, тем не менее в ряде случаев подобные квазиоптические линии передачи могут ...
... М.Н. ________________ «___»__________1996г. Д И П Л О М Н А Я Р А Б О Т А «Возможности радиолокационного тренажера NMS-90 и его использование для решения задач расхождения в условиях ограниченной видимости» ШИФР _________________ ИСПОЛНИТЕЛЬ ...
... : ¾ температура, °С +25±10; ¾ относительная влажность воздуха, % 45...80; ¾ атмосферное давление, мм рт. ст. 630...800. Так как блок интерфейсных адаптеров предназначен для работы в нормальных условиях, в качестве номинальных значений климатических факторов указанные выше принимают нормальные значения ...
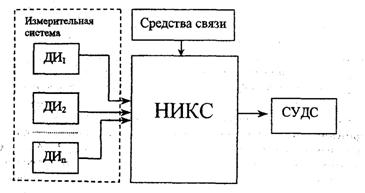
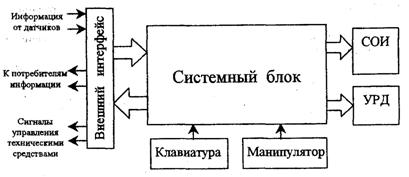
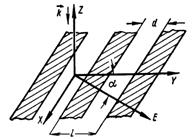
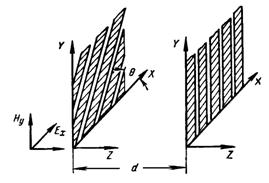
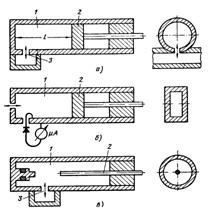




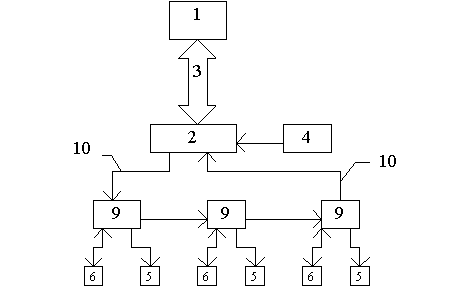
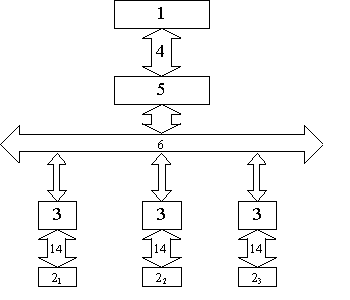
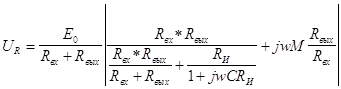


0 комментариев