Навигация
Определение фазочастотной характеристики цепи
2.3 Определение фазочастотной характеристики цепи
Фазочастотная характеристика цепи (ФЧХ):
|
| (16) |
Подставляя числовые значения в (16) получим:
|
| (17) |
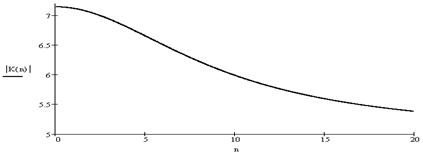
Результаты расчётов приведены в таблице 2.2, а кривая, построенная на основании результатов, имеет вид графика изображённого на рисунке 2.2
| Таблица 2.2 | Зависимость ArgK(jw) от частоты |
| w, рад/с | ArgK(jw), рад |
| 0 | 0 |
| 1*10^7 | -0.0799271 |
| 3*10^7 | -0.3226808 |
| 5*10^7 | -0.6462386 |
| 7*10^7 | -0.9086729 |
| 9*10^7 | -1.0769648 |
| 1.1*10^8 | -1.1826898 |
| 1.3*10^8 | -1.2524606 |
| 1.5*10^8 | -1.3011954 |
| 1.7*10^8 | -1.3369474 |
| 1.9*10^8 | -1.3642366 |
| 2.1*10^8 | -1.3857381 |
| 2.3*10^8 | -1.4031184 |
| 2.5*10^8 | -1.4174637 |
| 2.7*10^8 | -1.42951 |
| 2.9*10^8 | -1.4397731 |
| 3.1*10^8 | -1.4486249 |
| 3.3*10^8 | -1.4563401 |
| 3.5*10^8 | -1.4631264 |
| 3.7*10^8 | -1.4691435 |
| 3.9*10^8 | -1.4745161 |
| 4.1*10^8 | -1.4793434 |
| 4.3*10^8 | -1.483705 |
| 4.6*10^8 | -1.4895127 |
| 4.8*10^8 | -1.492969 |
| 5*10^8 | -1.4961411 |
| 5.2*10^8 | -1.4990628 |
| 5.4*10^8 | -1.5017629 |
| 5.6*10^8 | -1.5042658 |
| 5.8*10^8 | -1.5065924 |
| 6*10^8 | -1.5087609 |
|
| -1,5707963 |
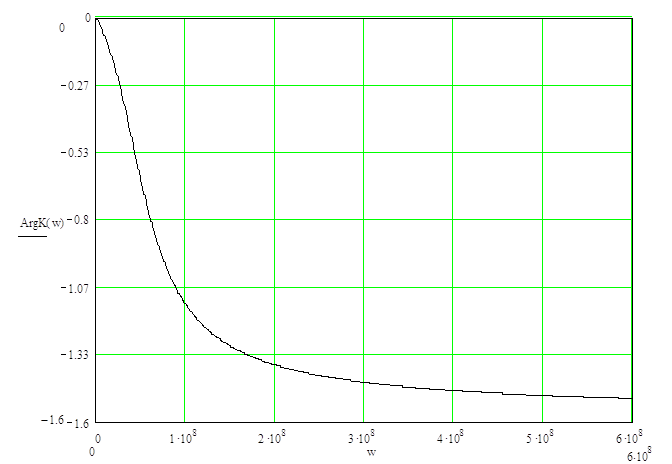
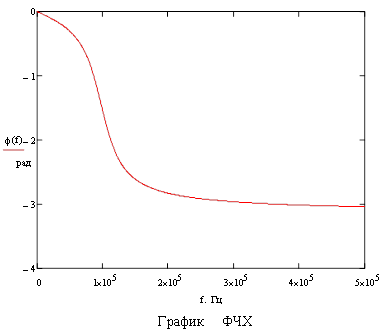
Рисунок 2.2 ‑ ФЧХ цепи; размерность ArgK(w) – рад, w – рад/с
3 РАСЧЕТ ВРЕМЕННЫХ ХАРАКТЕРИСТИК ЦЕПИ
3.1 Определение переходной характеристики цепи
Переходная характеристика цепи:
| h(t)=hпр(t)+hсв(t) | (18) |
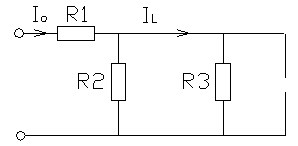
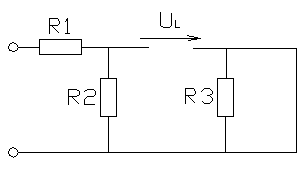
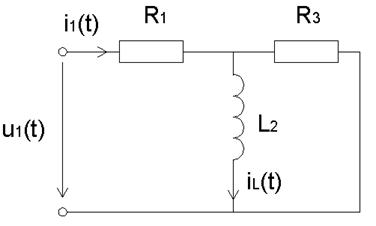
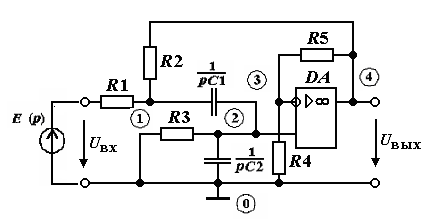
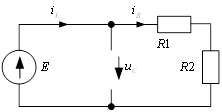
Т.к. воздействие – ток, а реакция – ток на индуктивности, следует (см. рисунок 3.1):
|
| (19) |
 |
где Io – единичный скачок тока.
Для определения режима переходного процесса запишем входное сопротивление в операторной форме:
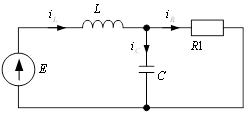
Рисунок 3.1‑Эквивалентная схема при t стремящемся к бесконечности
|
| (20) |
Приравнивая знаменатель к нулю, после несложных преобразований получим:
![]() или
или ![]() ,
,
где:
|
| (21) |
|
| (22) |
Т.к. ![]() , следует режим колебательный, а значит:
, следует режим колебательный, а значит:
|
| (23) |
| где:
| (24) |
– угловая частота затухающих свободных колебаний в контуре, А и ![]() ‑ постоянные интегрирования.
‑ постоянные интегрирования.
Для определения постоянных интегрирования составим два уравнения для начальных значений ![]() (+0) и
(+0) и ![]() (+0):
(+0):
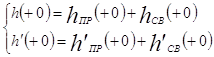 (25),
(25), ![]() (26) (см.
(26) (см.
рисунок 3.2),
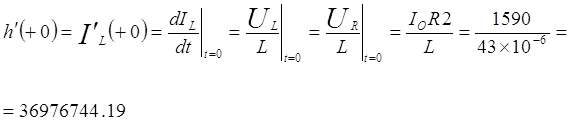 (27),
(27),
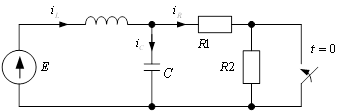
т.к. в момент комутации напряжение на сопротивлении R2 равно напряжению на индуктивности (см. рисунок 3.2).
|
| (28) |
|
| (29) |
Рисунок 3.2 – Эквивалентная схема в момент коммутации
Подставляя выражения (19), (21), (23), (24), (26), (27), (28), (29) в (25) получим:
|
| (30) |
|
|
| (31) |
|
|
| (32) |
|
![]() (33)
(33)
Результаты расчётов приведены в таблице 3.1, а кривая, построенная на основании результатов, имеет вид графика изображённого на рисунке 3.3
| Таблица 3.1 | Расчёт переходной характеристики |
| t, с | h(t) |
| 0 | 0 |
| 1.00e-8 | 0.303504193 |
| 2.00e-8 | 0.489869715 |
| 4.00e-8 | 0.632067650 |
| 5.00e-8 | 0.642131278 |
| 7.00e-8 | 0.624823543 |
| 8.00e-8 | 0.613243233 |
| 1.00e-7 | 0.597388596 |
| 1.10e-7 | 0.593357643 |
| 1.30e-7 | 0.590241988 |
| 1.40e-7 | 0.590004903 |
| 1.70e-7 | 0.590600383 |
| 1.90e-7 | 0.590939689 |
| 2.00e-7 | 0.591026845 |
| 2.20e-7 | 0.591095065 |
| 2.30e-7 | 0.591100606 |
| 2.50e-7 | 0.591093538 |
| 2.60e-7 | 0.591088357 |
| 2.80e-7 | 0.591081098 |
| 3.00e-7 | 0.591078184 |
|
| 0.591078066 |
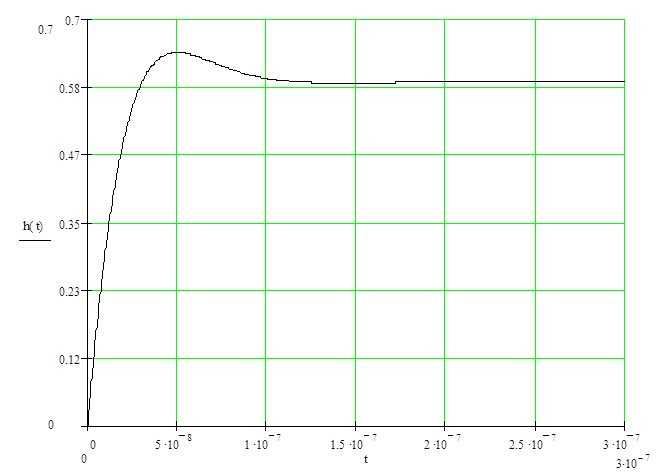
Рисунок 3.3 – Переходная характеристика цепи; размерность t – сек,
h(t) – безразмерная величина
Как видно из рисунка 3.3, свободные колебания затухают достаточно быстро; при таком масштабе рисунка видны колебания в течение, примерно, одного периода свободных колебаний (![]() ), однако переходной процесс длится немного дольше, а спустя 0,3 мкс колебаниями можно пренебречь т.к. они достаточно малы (см. таблицу 3.1) и считать переходной процесс завершенным.
), однако переходной процесс длится немного дольше, а спустя 0,3 мкс колебаниями можно пренебречь т.к. они достаточно малы (см. таблицу 3.1) и считать переходной процесс завершенным.
Похожие работы
... специалистов, которые проектируют электронную аппаратуру. Курсовая работа по этой дисциплине - один из этапов самостоятельной работы, который позволяет определить и исследовать частотные и временные характеристики избирательных цепей, установить связь между предельными значениями этих характеристик, а также закрепить знания по спектральному и временному методам расчета отклика цепи. 1. Расчёт ...
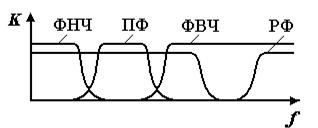
... t, мкс m=100 1.982*10-4 19,82 m=100000 1,98*10-4 19,82 Временные характеристики исследуемой цепи изображены на рис.6, рис. 7. Частотные характеристики изображены на рис. 4, рис. 5. ВРЕМЕННОЙ МЕТОД АНАЛИЗА 7. ОПРЕДЕЛЕНИЕ РЕАКЦИИ ЦЕПИ НА ИМПУЛЬС С помощью интеграла Дюамеля можно определить реакцию цепи на заданное воздействие и в том случае, когда внешнее воздействие на ...
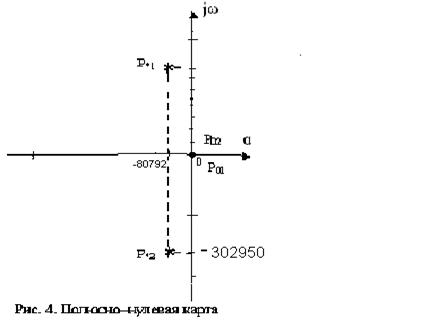
... -частотной характеристики : Дб/дек Дб/дек н=39300 Гц н=63300Гц →63300-39300=24000Гц Расчет частотных характеристик всегда проводят в определенном диапазоне частот, в котором проявляются основные частотные свойства электрической цепи. Величину диапазона частот можно определить по полюсно-нулевой карте операторной функции. В качестве нижней ...
... . В линейной цепи – это линейные дифференциальные уравнения (ЛДУ). Существуют различные методы решения таких уравнений, и соответственно различают различные методы расчета переходных процессов. 2 Способы получение характеристического уравнения Классический метод Классический метод основан на решении ЛДУ методом вариации произвольных постоянных. Любая система ЛДУ может быть сведена к одному ...
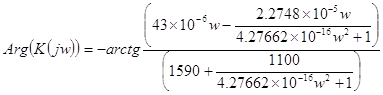
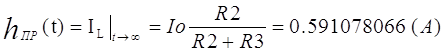 ,
,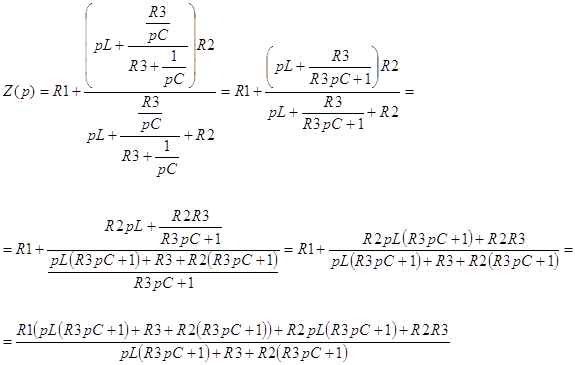
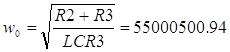 (рад/с)
(рад/с)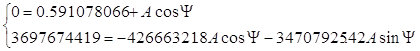

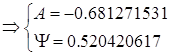
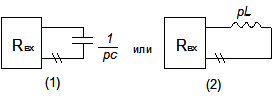
0 комментариев