Навигация
Корневые критерии заключаются в вычислении корней
1.4.1 Корневые критерии заключаются в вычислении корней
характеристического полинома замкнутой системы.
1.4.2 Алгебраические критерии устойчивости не требуют выполнения вычислительной процедуры определения корней характеристического уравнения и при относительно невысоких порядках дифференциальных уравнений (до 15-го) позволяют находить условия устойчивости автономных замкнутых систем.
А(s)=ansn + an-1sn-1+ an-2sn-2+…+a0. (1.11)
Критерий Гурвица. Корни характеристического уравнения (1.11) n-го порядка будут иметь отрицательные действительные части, если составленный из его коэффициентов аi> 0 определитель
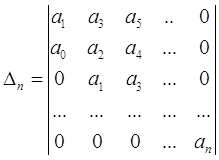 (1.12)
(1.12)
и все его диагональные миноры
 (1.13)
(1.13)
положительны.
Критерий Рауса. Зная коэффициенты характеристического уравнения, составляют таблицу Рауса(табл. 1.1). Для того чтобы замкнутая система была устойчива асимптотически, необходимо и достаточно, чтобы все коэффициенты Рауса первого столбца таблицы при аi>0 были положительны, т.е. сi,1>0 (i=1,2,…). Для вычисления элементов табл. 1.1 можно использовать следующие рекуррентные формулы:
для первой строки таблицы
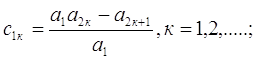 (1.14)
(1.14)
для второй строки таблицы
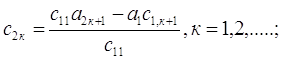
![]() (1.15)
(1.15)
для остальных строк
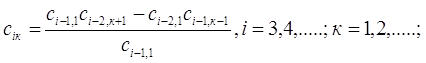 (1.16)
(1.16)
Таблица 1.1
| Номера строк | Номера столбцов | ||||
| 1 | 2 | 3 | ……. | I | |
| Коэффициенты с четными индексами | |||||
| а0 | а2 | а4 | ……. | ||
| Коэффициенты с нечетными индексами | |||||
| а1 | а3 | а5 | …….. | ||
| 1 | С11 | С12 | С13 | …….. | С1i |
| 2 | С21 | С22 | С23 | …….. | C2i |
| …. | …… | ….. | ….. | ……. | …… |
| к | Ск1 | Ск2 | Ск3 | …….. | Сiк |
Критерий Шур-Кона. Данный критерий позволяет анализировать устойчивость дискретных и дискретно-непрерывных систем по характеристическому полиному замкнутой системы, записанному в форме z-преобразования. Для уравнения n-го порядка имеем
A(z)=anzn+ an-1zn-1+ an-2zn-2+…+a0. (1.17)
По уравнению запишем коэффициенты в виде определителя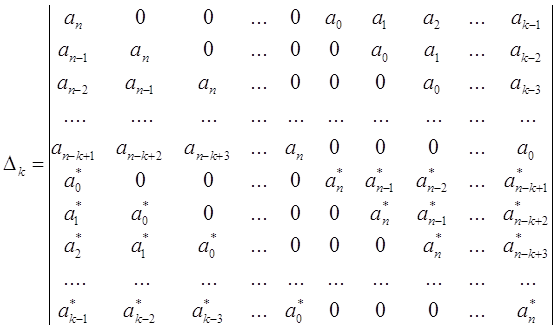 (1.18)
(1.18)
где k=1,2,…,n; a*- сопряженные значения тех же коэффициентов.
Корни характеристического уравнения (1.18) будут находиться внутри единичной окружности, если коэффициенты уравнения (1.17) удовлетворяют всем определителям Шур-Кона, имеющего Dk< 0 - для нечетных k и Dk > 0 для четных k. В этом случае система будет устойчива
Критерий Кларка. Представляет собой совокупность 3-х необходимых условий, и лишь выполнение всех этих условий является условием устойчивости системы:
1. А(1) > 0
2. (-1)А(-1) > 0
3. Необходимо вычислить определители матриц D+ и D- , а также их внутренние матрицы. Внутренние матрицы получаются из исходных вычеркиванием окаймляющих строк и столбцов. Количество условий устойчивости зависит от порядка системы.
D+=Cn-1+Bn-1; D-=Cn-1-Bn-1; (1.19)
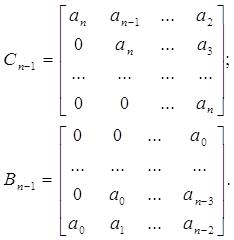 (1.20)
(1.20)
Похожие работы
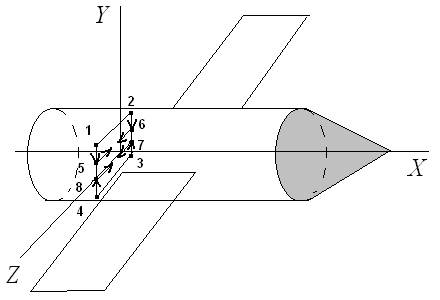
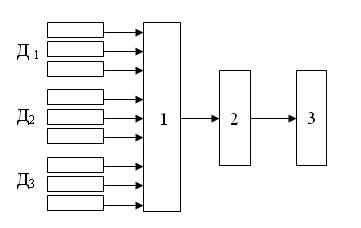
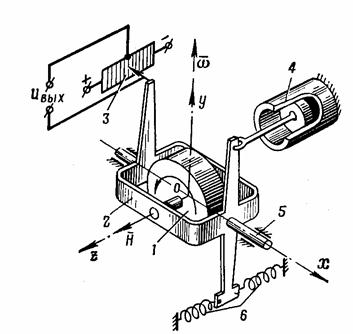
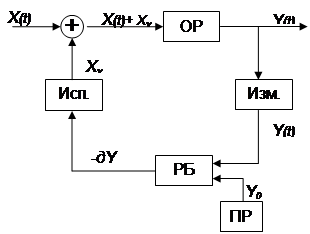
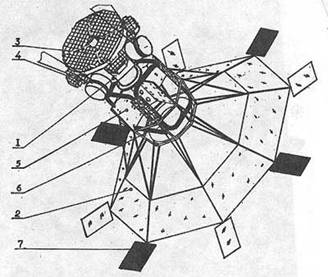
... , может приводить к большим потерям рабочего тела и раскрутке космического аппарата до недопустимых угловых скоростей. Таким образом разработка алгоритмов контроля и диагностики системы управления ориентацией космического аппарата – является актуальной задачей. В настоящей работе решается задача построения алгоритмов контроля и идентификации отказов командных приборов и исполнительных органов. ...
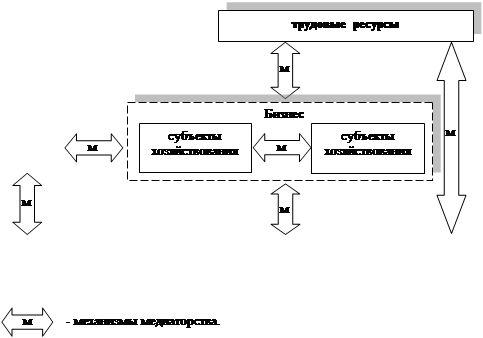
... процессов. Формирование институтов согласования интересов хозяйствующих субъектов на основе осуществления медиаторской деятельности, выступающей механизмом обеспечения институциональной устойчивости социально-экономической системы, наиболее значимо для экономических систем регионального уровня, что определяется спецификой организационно-управленческих связей хозяйственных образований данного ...
... — практической специализации, в процессе которой студенчество получает профессиональное образование, ибо оно послужит ему в дальнейшем в деле адаптации и социализации. 2. Особенности формирования ценностных ориентаций студенчества в КНР и России: сравнительный анализ 2.1 Содержание реформ: политические, экономические и социальные изменения в России и КНР 2.1.1 Содержание и итоги реформ ...
... поиск должен быть одним из важнейших ориентиров при формировании современной программы исследования космического пространства. Информация о реликтовом веществе в начальный период образования Солнечной системы будет способствовать углублению наших знаний о больших планетах, которые сформировались из мельчайших небесных тел, содержавших данное вещество. Таким образом, химический и физический анализы ...
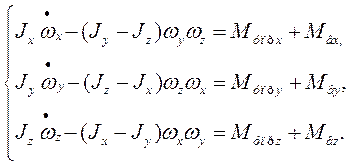
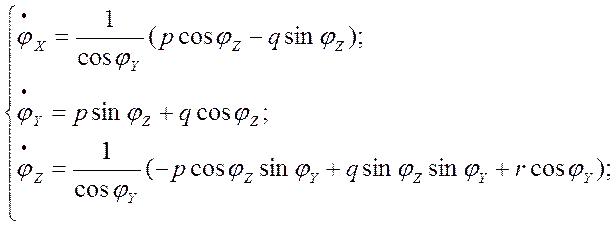

0 комментариев