Навигация
Обыкновенный процент и приблизительная продолжительность периода (T=360, t–приблизительное, когда считается, что в месяце 30 дней);
3. Обыкновенный процент и приблизительная продолжительность периода (T=360, t–приблизительное, когда считается, что в месяце 30 дней);
2.1.2. Наращение капитала по сложным процентам (декурсивный метод): а) начисление
процентов один
раз в году:
![]() ;
;
б) начисление
процентов m раз в году: 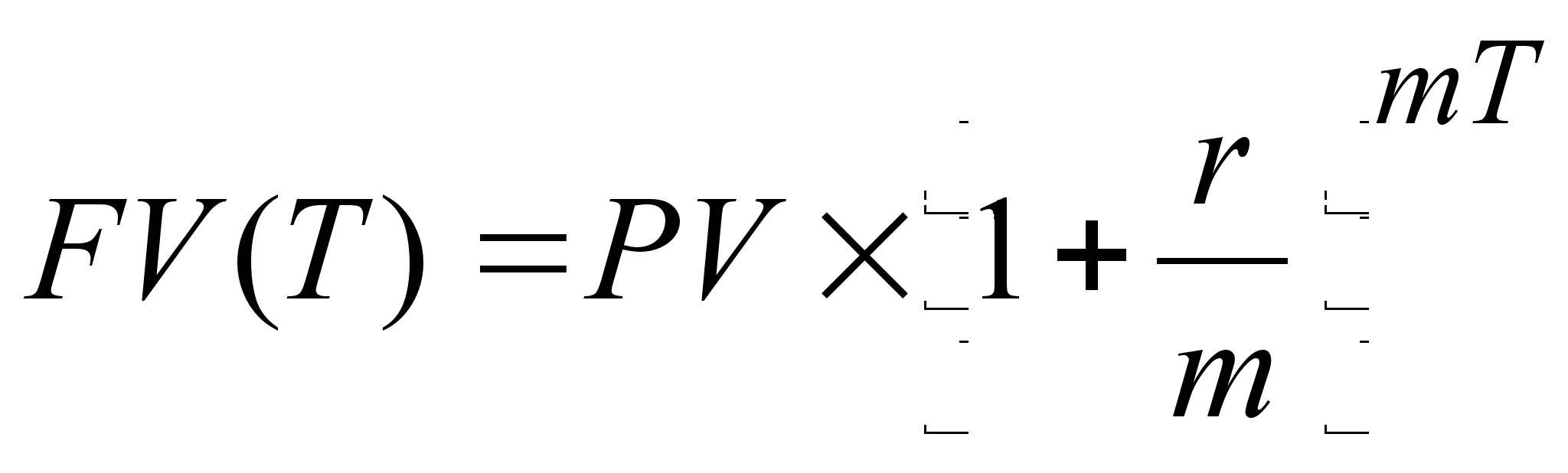 ;
;
в) Если
срок инвестиций
не является
целым числом,
тогда ![]() , где целое чисто
лет [T],
а {T}
– часть срока
сверх целого
числа лет (в
годах):
, где целое чисто
лет [T],
а {T}
– часть срока
сверх целого
числа лет (в
годах):
![]()
Определение: годовая ставка сложных процентов, дающая то же соотношение между выданной суммой PV и суммой FV, что и при любой схеме выплат называется эффективной.
а) Общий
случай: 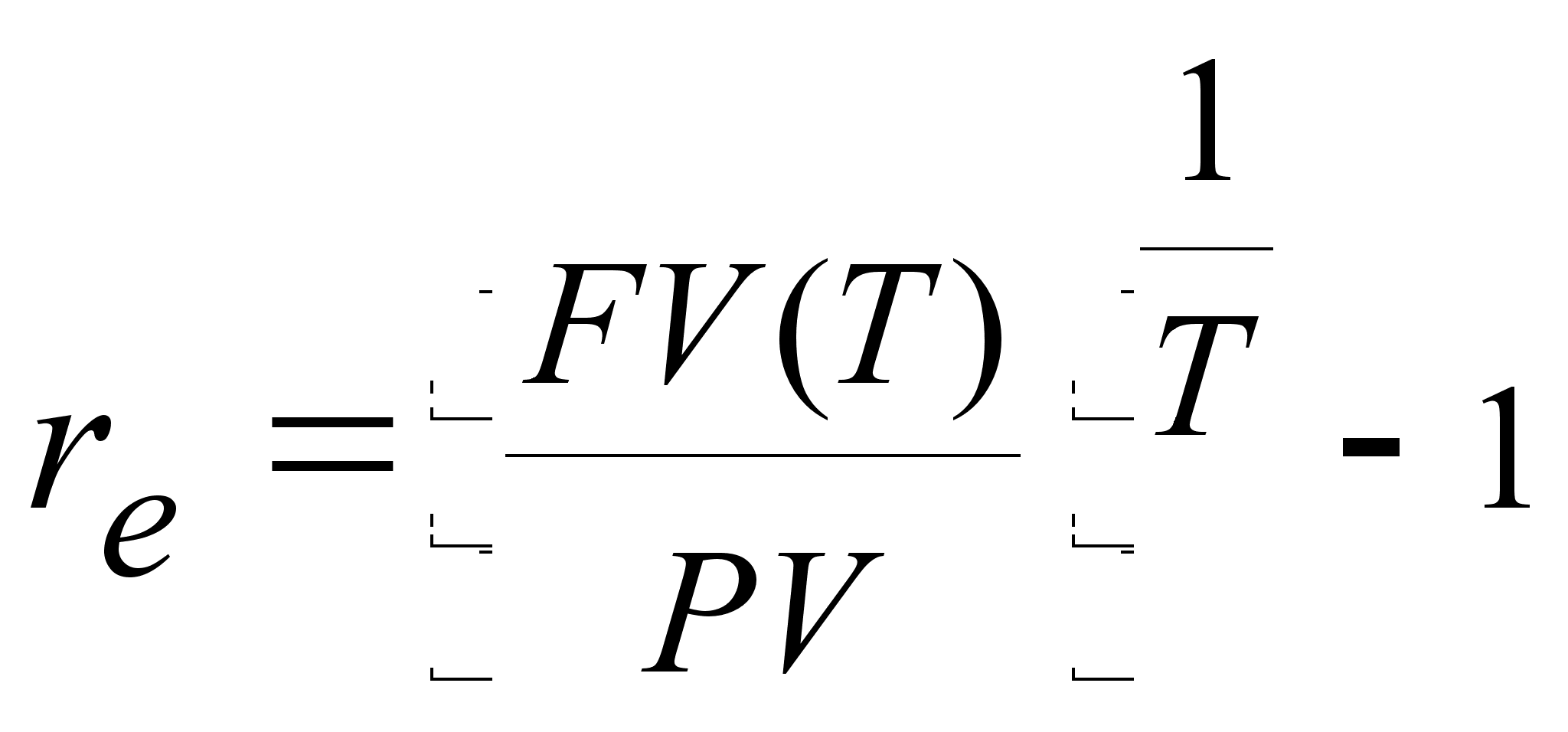 ;
;
б) наращение
по сложным
процентам с
начислением
m раз в году: 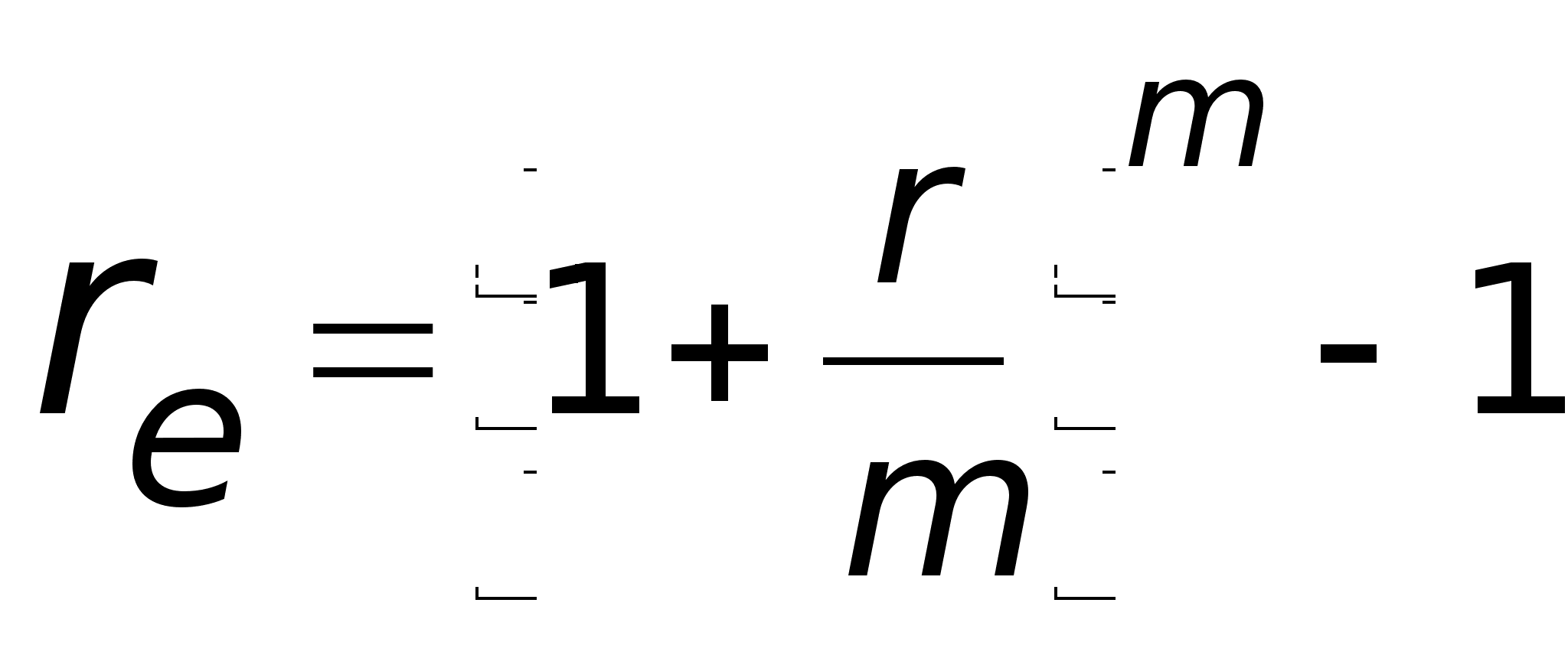 .
.
начисление процентов 1 раз в году по простым процентам:![]()
Очевидно, что должно
выполняться
условие: ![]() ,
т.е.
,
т.е. ![]() .
.
начисление процентов за период менее года( либо при не целом Т): 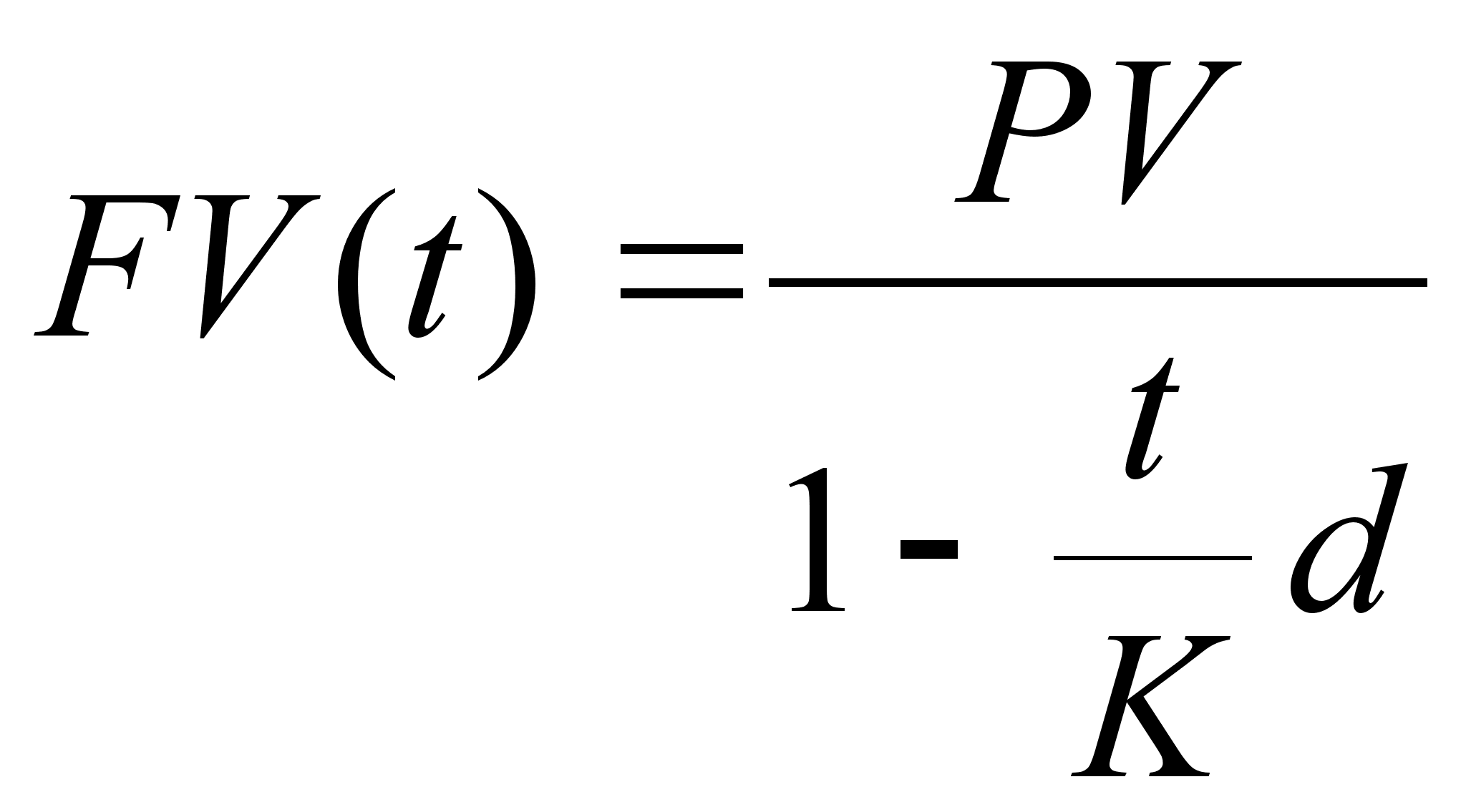
начисление по сложным процентам 1 раз в году: ![]() .
.
начисление по сложным процентам m раз в году: 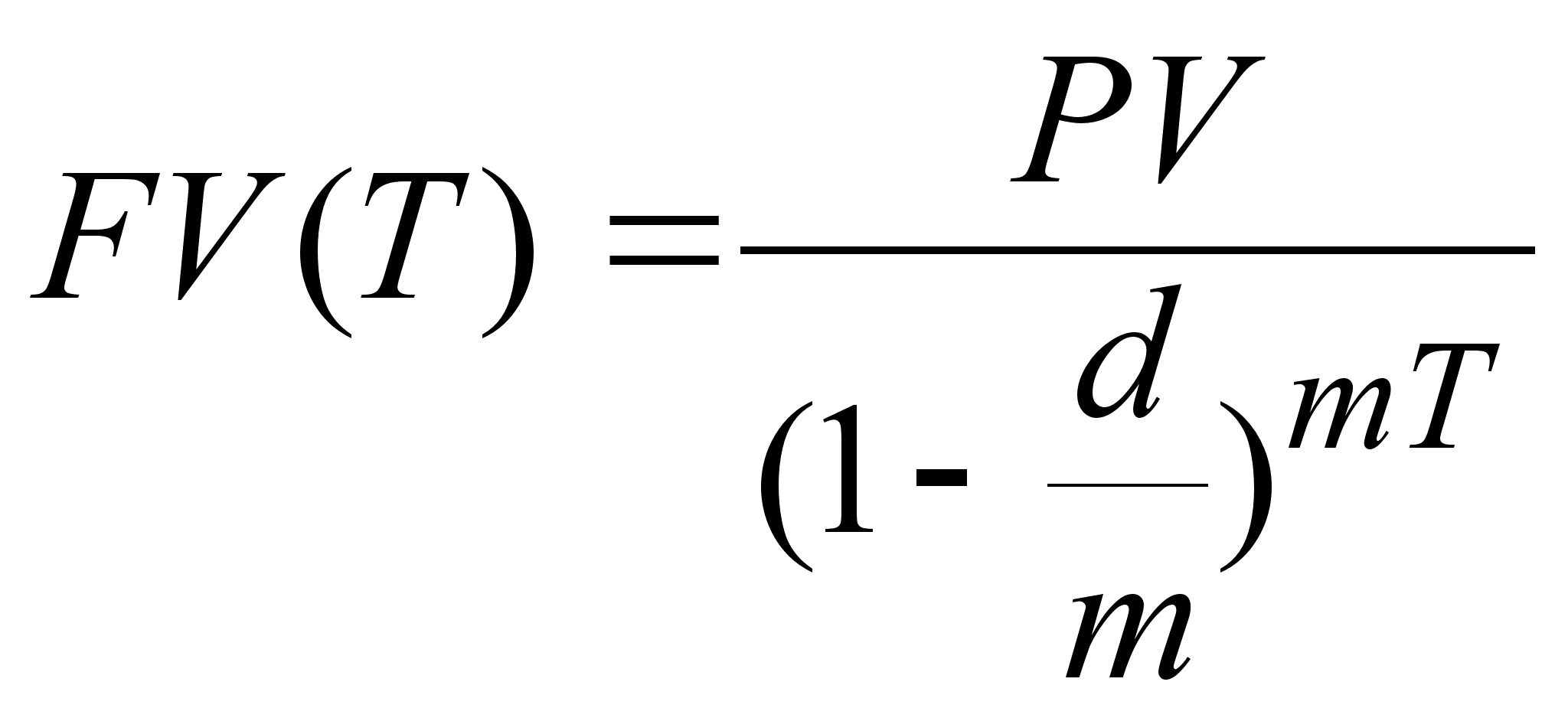
В финансовой практике часто сталкиваются с задачей обратной наращению процентов: по заданной сумме FV, которую следует уплатить через время T; необходимо определить сумму получаемой ссуды PV
Параметры операции: T– длительность финансовой операции (измеряется в годах), r–годовая ставка ссудного процента; d– учетная ставка (ставка дисконта)
PV-современная стоимость будущей суммы FV;
2.1. Математическое дисконтирование (с применением ставки ссудного процента –r)
а) по
ставке простого
процента:
![]()
б) по ставке
сложного процента
с начислением
один раз в году: ![]()
в) по ставке
сложного процента
с начислением
m
раз в году:
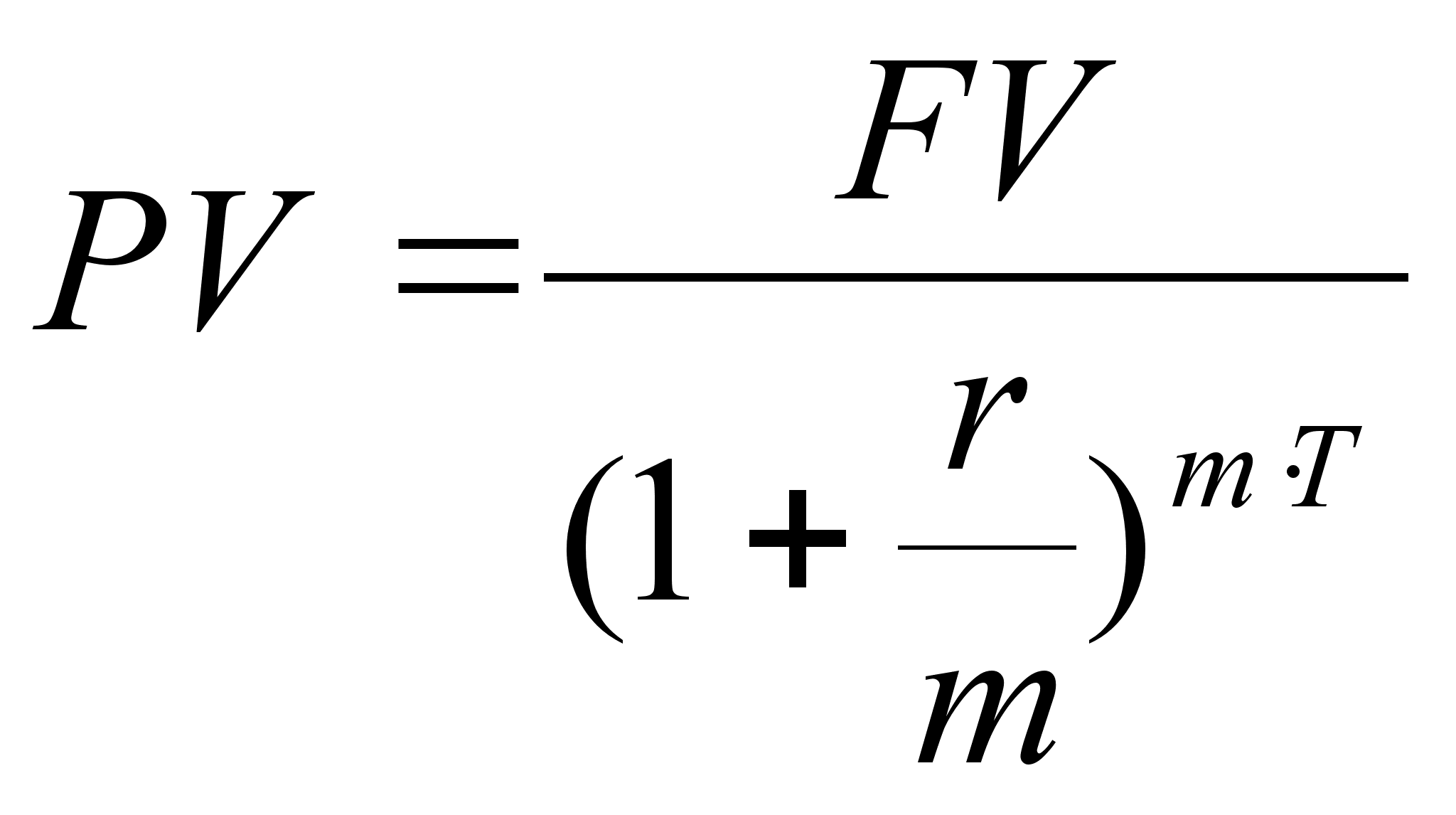
(Применяется схема дисконтирования с использованием учетной ставки d. )
Простые проценты: ![]() . В этой схеме чаще всего используется способ 365/360.
. В этой схеме чаще всего используется способ 365/360.
Сложные проценты с начислением 1 раз в году:![]()
Сложные проценты с начислением m раз в году:![]()
3. Определение параметров (r, T,d) простейшей финансовой операции
Для определения ставки ссудного процента, учетной ставки или срока проведения операций необходимо воспользоваться формулами наращения или дисконтирования, из которых находится искомый параметр.
![]() PV
и FV в этом случае
заданы.
PV
и FV в этом случае
заданы.
Тема. Анализ операции наращения процентов
Задание
Провести анализ операции наращения по простым декурсивным процентам с разными временными базами(360/360; 365/365; 365/360) и разных сроках операциию. Построить таблицу.
Провести анализ операции наращения по сложным декурсивным процентам, выбирая разные периоды начисления процентов (1 раз в год, 2,4,12 раз в год).
Сравнить результаты начисления сложных процентов при нецелом числе лет с комбинированным вариантом (при различных сроках операции; при различных периодах начисления). Построить таблицы.
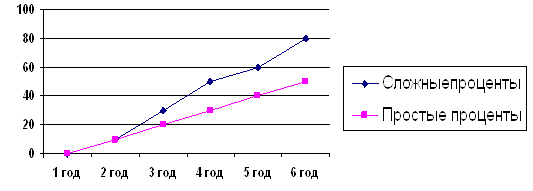
Построить таблицы зависимости и графики коэффициента наращения по сложным и простым декурсивным процентам при различных ставках процента.
Рассчитать эффективные ставки для схем начисления по простым и сложным декурсивным процентам при различных сроках операции. Построить таблицу зависимости.
Рассчитать и сравнить эффективные ставки для операций наращения по сложным декурсивным процентам с периодичностью начисления 1 раз в году, m раз в году. Построить таблицу зависимости.
Провести сравнительный анализ операций наращения по декурсивному и антисипативному методу в зависимости от срока и ставки простых процентов. Построить таблицу зависимости и дать графическую иллюстрацию.
Провести сравнительный анализ операций наращения по декурсивному и антисипативному методу в зависимости от срока и ставки сложных процентов. Построить таблицу зависимости и дать графическую иллюстрацию
Для проведения расчетов разработать специальные шаблоны.
Для построения таблицы зависимости воспользуйтесь таблицами постановки.
Лабораторная работа № 2.Тема:. Анализ процесса дисконтирования. Определение параметров простейших финансовых операций
Задание
Провести анализ операции математического дисконтирования в зависимости от срока операции и процентной ставки, используя схемы простого и сложного процентов с начислением один раз в году. Построить таблицы зависимостей и дать графическую иллюстрацию (построить графики коэффициентов приведения).
Построить графики коэффициента приведения при математическом дисконтировании по сложным и простым процентам (при одинаковой ставке процента).
Провести анализ операции дисконтирования с использованием учетной ставки по простым и сложным процентам, сравнить с аналогичной операцией при использовании ставки ссудного процента. (Построить таблицы зависимостей и дать графическую иллюстрацию)
Определение ставки процента в схемах наращения и дисконтирования с использованием декурсивных и антисипативных процентов. Результаты представить в виде таблицы.
Определение срока операции в схемах наращения и дисконтирования с использованием декурсивных и антисипативных процентов. Результаты представить в виде таблицы
Сравнить операции дисконтирования с применением ставки ссудного процента и учетной ставки. Построить графики коэффициентов приведения. Результаты представить в виде таблицы
| Для построения таблицы зависимости воспользуйтесь таблицами постановки |
| |
13
Лабораторная работа № 3. Потоки платежей (аннуитеты)
Поток платежей, все элементы которого распределены во времени так, что интервалы между любыми двумя последовательными платежами постоянны, называют финансовой рентой или аннуитетом (annuity).
Ренты характеризуются следующими параметрами:
A– член ренты, т.е. величина каждого годового платежа,
p - число платежей в году,
m– число начислений процентов в году,
T– срок ренты в годах (время от начала ренты до конца последнего периода выплат).
t–период ренты (временной интервал между двумя последовательными платежами,
r–годовая ставка процента;
FV– наращенная сумма (сумма всех членов потока платежей с начисленными на них к концу срока процентами);
PV– приведенная (современная) стоимость потока платежей–это сумма всех его членов, дисконтированных на начало срока ренты или некоторый упреждающий момент времени
Если платежи осуществляются в конце периода, имеем ренту постнумерандо, в начале периода– пренумерандо. Если платежи осуществляются равномерно в течении периода, то считают, что платеж приурочен к середине периода, а ренту называют равномерной.
Основные формулы наращения| Виды рент | Наращение постнумерандо FV | Наращение пренумерандо |
| Годовая с начислением % 1 раз в году (р=1, m=1 ) | | |
| Годовая с начислением % m раз в году (р=1, m1 ) | | |
| Рента р–срочная c начисленим % один раз в году (р1, m=1 ). | | |
| Рента р–срочная c начисленим % m раз в году (р1, m1,p=m). | | |
| Рента р–срочная c начисленим % m раз в году (р1, m1,pm). | | |
| Рента годовая c непрерывным начисленим %(p=1, | | |
| Рента P–срочная c непрерывным начисленим %( р1, | | |
Отличие постоянных
рент пренумерандо
от рент поснумерандо
состоит в том,
что время начисления
процентов на
каждую выплату
увеличивается
на один период
ренты, следовательно,
сумма наращения ![]() будет
больше, чем
сумма FV
в S(1,r)
раз, где S(1,r)
– множитель
наращения
платежа за один
период, соответствующей
данному типу
ренты.
будет
больше, чем
сумма FV
в S(1,r)
раз, где S(1,r)
– множитель
наращения
платежа за один
период, соответствующей
данному типу
ренты.
Это же правило сохраняется и для приведенных стоимостей указанных рент
Основные формулы приведения
| Виды рент | Приведение постнумерандо PV | Приведение пренумерандо |
| Годовая с начислением % 1 раз в году (р=1, m=1 ) | | |
| Годовая с начислением % m раз в году (р=1, m1 ) | | |
| Рента р–срочная c начисленим % один раз в году (р1, m=1 ). | | |
| Рента р–срочная c начисленим % m раз в году (р1, m1,p=m). | | |
| Рента р–срочная c начисленим % m раз в году (р1, m1,pm). | | |
| Рента годовая c непрерывным начисленим %(p=1, | | |
| Рента P–срочная c непрерывным начисленим %( р1, | | |
Группу функций EXCEL, предназначенную для автоматизации расчетов характеристик аннуитетов, составляют функции, применяемые в анализе простейших финансовых операций: БЗ(), КПЕР(), НОРМА(), ПЗ() (см. табл. 1.1), к которым добавляется функция определения периодического платежа – ППЛАТ().
Функция ППЛАТ(ставка; кпер; нз; [бс]; [тип])
Данная функция применяется в том случае, если необходимо определить величину периодического платежа – A.
В случае, если условиями контракта предусмотрено начисление процентов в начале каждого периода, при исчислении любой характеристики финансовой операции необходимо задавать аргумент “тип”, равный 1.
Отметим, что начисление процентов в начале каждого периода всегда приводит к большему значению будущей величины аннуитета за тот же срок.
При начислении процентов m-раз в году, величины r и n корректируются также, как и в случае простой финансовой операции.
ЗаданиеЗадавая параметры рент, найти наращенные суммы и приведенные стоимости всех перечисленных в таблице рент.
Проанализировать, как меняется наращенная сумма рент в зависимости от годовой процентной ставки, числа начислений процентов, числа платежей. Составить таблицы для сравнения.
Проанализировать, как меняется современная стоимость рент в зависимости от годовой процентной ставки, числа начислений процентов, числа платежей. Составить таблицы для сравнения.
Для различных видов рент, найти недостающий параметр величину платежа, срок ренты или годовую ставку процентов.
Для решения этой задачи воспользоваться соответствующими функциями EXCEL или вывести формулу нахождения соответствующего параметра, используя формулы наращения или приведения рент.
Задать темп инфляции постоянный в течение срока ренты и провести сравнительный анализ процесса наращения без инфляции и с инфляцией. Рассчитать барьерную и брутто ставки. Проделать то же самое, но при изменяющемся ежеквартально темпе инфляции.
Задать темп инфляции постоянный в течение срока ренты и провести сравнительный анализ получающихся приведенных стоимостей без инфляции и с инфляцией с постоянным и переменным темпом
Лабораторная работа 4 Тема. 3 Денежные потоки в виде серии платежей произвольной величиныДенежные потоки в виде платежей произвольной величины, осуществляемые через равные промежутки времени, представляют собой наиболее общий вид аннуитетов.
Суммарная
величина потока
рассчитывается
по исходному
потоку: F1,F2,...,Fn.
по формуле: ![]()
Современная
стоимость
потока по формуле: ![]()
Финансовая операция может также предусматривать неоднократные и разновременные переходы денежных сумм от одного владельца к другому. Рассматривая поток платежей с позиций одного из них, можно считать все поступления к нему положительными величинами, а все выплаты– отрицательными. Для оценки финансовой операции в целом используется чистая приведенная величина NPV, вычисляемая по формуле:
![]() ,
но с учетом
знака Fi.
,
но с учетом
знака Fi.
Таблица 1.4
| Наименование функции | Формат функции | |
| Оригинальная версия | Локализованная версия | |
| NPV | НПЗ | НПЗ(ставка; платежи) |
| IRR | ВНДОХ | ВНДОХ(платежи; [прогноз]) |
| MIRR | МВСД | МВСД(платежи;ставка;ставка_реин) |
| XNPV | ЧИСТНЗ | ЧИСТНЗ(ставка; платежи; даты) |
| XIRR | ЧИСТВНДОХ | ЧИСТВНДОХ(платежи;даты;[прогноз]) |
Обязательные для задания аргументы функций имеют следующие значения:
ставка – процентная ставка (норма прибыли или цена капитала);
платежи – поток из n - платежей произвольной величины;
ставка_реин – ставка реинвестирования полученных средств;
даты – массив дат осуществления платежей для потоков с произвольными интервалами времени.
Функции данной группы используют сложные итерационные алгоритмы для реализации дисконтных методов исчисления ряда важнейших показателей, широко используемых в инвестиционном анализе.
Первые три функции применяются в том случае, когда денежный поток состоит из платежей произвольной величины, осуществляемых через равные промежутки времени.
Функция НПЗ() вычисляет современную величину потока платежей PV. Две другие функции – ВНДОХ() и МВСД() позволяют определить внутреннюю норму рентабельности инвестиций (internal rate of return – IRR) и модифицированную внутреннюю норму рентабельности инвестиций (modified internal rate of return – MIRR) соответственно.
Функции ЧИСТНЗ( ) и ЧИСТВНДОХ( ) являются самыми мощными в рассматриваемой группе. Они позволяют определить показатели чистой современной стоимости (net present value – NPV) и внутренней нормы рентабельности IRR для потоков платежей произвольной величины осуществляемых за любые промежутки времени. Эти функции удобно использовать для ретроспективного анализа эффективности операций с ценными бумагами, периодический доход по которым выплачивается по плавающей ставке (например – ОГСЗ, ОФЗ и т.д.). Детальное описание технологии их применения можно посмотреть в «справке к EXCEL».
Задание.
1. Рассчитать конечную и приведенную сумму потока платежей с неравными поступлениями через равные промежутки времени. Вычислить внутреннюю норму рентабельности.
2. Рассмотреть инвестиционный проект с одноразовой инвестицией в начале первого периода ( в конце первого периода) и выплатами в начале (конце) с третьего по шестой год и рассчитать для него NPV и IRR, срок окупаемости и индекс рентабельности
3. Рассмотреть инвестиционный проект с инвестициями в течение m лет через неравные промежутки времени и поступлениями дохода после окончания инвестиций с m+1 года в течение n лет и рассчитать NPV и IRR, срок окупаемости и индекс рентабельности.
4. Проанализировать изменение NPV от выбранной ставки процента r и срока поступлений платежей (при одинаковой общей сумме). Использовать таблицы подстановки.
Литература
Базисные финансовые расчеты
Е.М. Четыркин, Н.Е. Васильева. Финансово-экономические расчеты. Справочное пособие. М.: Финансы и статистика, 1990.
Е.М. Четыркин. Методы финансовых и коммерческих расчетов. М.: Дело ЛТД, 1995.
В.Е. Черкасов. Практическое руководство по финансово-экономическим расчетам. М.: МЕТАИНФОРМ: АО "Консалтингбанкир", 1995.
Кредит. Ценные бумаги с фиксированным доходом
М.В. Лычагин. Финансы и кредит. Популярно о сложном. Новосибирск, изд-во НГУ, 1992.
В.С. Волынский. Кредит в условиях современного капитализма. М.: Финансы и статистика, 1991.
Ван Хорн, Джеймс. Основы управления финансами. М.: Финансы и статистика, 1996.
Н.Г. Антонов, М.А. Пессель. Денежное обращение, кредит и банки. М.: Финстатинформ, 1995.
Д.Л. Иванов. Вексель. М.: АО "Консалтбанкир", 1994.
А.А. Фельдман. Вексельное обращение. Российская и международная практика. М.: Инфра-М, 1995.
Вексель: 100 вопросов и ответов. М.: Менатеп-Информ, 1995.
Государственные и краткосрочные облигации: теория и практика рынка. М.: Моск. межб. валют. биржа, 1995.
Я.М. Миркин. Ценные бумаги и фондовый рынок. Профессиональный курс в финансовой академии при правительстве РФ. М.: Перспектива, 1995.
Иностранная валюта.
И.Т. Балабанов. Валютные операции. М., Финансы и статистика, 1993.
И.Т. Балабанов. Валютный рынок и валютные операции в России. М., Финансы и статистика, 1994.
И.Т. Балабанов. Основы финансового менеджмента. Как управлять капиталом? М., Финансы и статистика, 1994.
И.Т. Балабанов. Финансовый менеджмент. М., Финансы и статистика, 1994.
Э. Роде. Банки, биржи, валюты современного капитализма. М., 1986.
Б.Г. Федоров. Современные валютно – финансовые рынки. М., 1989.
М.В. Федоров. Валюта, валютные системы и валютные курсы. М., ПАИМС, 1995.
М. Бункина. Деньги. Банки. Валюта. М.: АО "ДИС", 1994.
М. Бункина. Валютный рынок. М.: АО "ДИС", 1995.
Т.Д. Валовая. Валютный курс и его колебания. М.: Финстатинформ, 1995.
А.Г. Ноговицин, В.В. Иванов. Валютный курс: Факторы. Динамика. Прогнозирование. М.: ИНФРА, 1995.
. Обыкновенные акции.
М.Ю. Алексеев. Рынок ценных бумаг. М., 1992.
Б.И. Алехин. Рынок ценных бумаг. Введение в фондовые операции. Самара, 1992.
А.Н. Буренин. Введение в рынок ценных бумаг. М., 1992.
В.Т. Мусатов. Фондовый рынок. Инструменты и механизмы. М., Международные отношения, 1991.
А. Ноздрачев. Регулирование рынка. М., 1991.
С.В. Павлов. Фондовая биржа и ее роль в экономике современного капитализма. М., Финансы и статистика, 1989.
А.А. Первозванский, Т.Н. Первозванская. Фондовый рынок: Расчет и риск. М., ИНФРА, 1994.
А.С. Чесноков. Рынок ценных бумаг, фондовые биржи, брокерская и дилерская деятельность. М., 1992.
Л. Энджел, Б. Бойд. Как покупать ценные бумаги. Самара, Самарский Дом Печати, 1993.
А. Эрлих. Технический анализ товарных и финансовых рынков. М.: ИНФРА-М, 1996.
Л.Дж. Гитман, М.Д. Джонк. Основы инвестирования. М., Дело, 1997.
У.Ф. Шарп, Г.Дж. Александер, Д.В. Бэйли. Инвестиции. М., ИНФРА-М, 1997.
Финансовые фьючерсы.
А.Н. Буренин. Фьючерсные, форвардные и опционные рынки. М.: Тривола, 1994.
Ф. Шварц. Биржевая деятельность запада (Фьючерсные и фондовые биржи, системы работы и алгоритмы анализа). М.,"Ай-Кью", 1992.
А.С. Чесноков. Инвестиционная стратегия, опционы и фьючерсы. М., НИИ Управления Мин. Экономики РФ, 1993.
А.С. Чесноков. Инвестиционная стратегия и финансовые игры. М., ПАИМС, 1994.
Финансовые фьючерсы. М., МГУ, Ассоциация "Гуманитарное знание", 1993.
Г.Г. Салыч. Опционные, фьючерсные и форвардные контракты. М., МГУ, 1994.
Опционы.
А.Н. Буренин. Фьючерсные, форвардные и опционные рынки.: Тривола, 1994.
А.С. Чесноков. Инвестиционная стратегия, опционы и фьючерсы. НИИ Управления Мин. Экономики РФ, 1993.
А.С. Чесноков. Инвестиционная стратегия и финансовые игры. М., ПАИМС, 1994.
Г.Г. Салыч. Опционные, фьючерсные и форвардные контракты. МГУ, 1994.
Арбитраж и хеждирование.
А.Н. Буренин. Фьючерсные, форвардные и опционные рынки. М.: Тривола, 1994.
Ф. Шварц. Биржевая деятельность запада (Фьючерсные и фондовые биржи, системы работы и алгоритмы анализа). М.,"Ай-Кью", 1992.
Р. Вейсвейллер. Арбитраж. Возможности и техника операций на финансовых и товарных рынках. М., Церих-Пэл, 1995.
Расчет премии опциона методом Монте-Карло.
Артемьев С.С., Михайличенко И.Г., Синицын И.Н. Статистическое моделирование срочных финансовых операций. - Новосибирск: Изд. ВЦ СО РАН, 1996.
А.Н. Буренин. Фьючерсные, форвардные и опционные рынки. М.: Тривола, 1994.
А.С. Чесноков. Инвестиционная стратегия, опционы и фьючерсы. М., НИИ Управления Мин. Экономики РФ, 1993.
Перечень тем курсовых работ по дисциплине « Финансовая математика»
Акции и их оценка.
Анализ различных подходов к выбору ставки дисконтирования в инвестиционном анализе.
Анализ устойчивости инвестиционных проектов.
Вероятностные финансовые операции и их оценка
Имитационное моделирование инвестиционных рисков.
Инвестиционные риски и методы их расчета.
Иностранная валюта и валютные рынки.
Инфляция и методы ее учета при реализации финансовых операций
Классификация и анализ экономических рисков при проведении финансово-экономического анализа инвестиционного проекта.
Количественный анализ риска инвестиционных проектов
Модели торгов.
Модели ценообразования активов.
Облигации. Определение их доходности и качества.
Опционы и ценообразование опционов.
Оценка экономической эффективности инвестиционных проектов
Финансовые фьючерсы.
Финансовый рынок и его модели
Формирование оптимального портфеля с помощью ведущего фактора финансового рынка.
Формирование эффективных портфелей ценных бумаг.
Анализ динамики и прогнозирование ставки рефинансирования Центрального банка.
Анализ динамики индекса потребительских цен.
Анализ доходности векселей (на примере какой либо корпорации)
Анализ динамики базовых ставок кредитования (на примере Сбербанка РФ).
Похожие работы
... . Переменные процентные ставки В некоторых случаях(каких) ставка может изменяться во времени, тогда формула начисления сложных процентов примет вид: S = P(1 + i)n1 (1 + i)n2 … (1 + i)nk. (7) Математическое дисконтирование P = S/(1+i)n (8) Р - первоначальная сумма долга; S - наращенная сумма, или сумма в конце срока; i - ставка наращения (десятичная дробь); n - срок ссуды. ...
... доходность – годовая процентная ставка, характеризующая полный относительный годовой доход по операции с учетом внутригодовой капитализации. ЗАКЛЮЧЕНИЕ Предлагаемое учебное пособие рассматривает финансовые вычисления, предметом которых является результат деятельности инвестиционных, биржевых, кредитных, страховых, валютных и иных заимствующих организаций. Эти финансовые вычисления называют ...
... и частных участков земли под застройку, для садово-огородных и дачных участков (с постройками) и для сельскохозяйственных угодий (мелких - до 0,2 га, средних - до 0,5 га, крупных - до 15 га). Рынок жилой недвижимости (жилищный рынок) обеспечивает обращение прав собственности или аренды - государственных, муниципальных, частных и коллективных жилых домов (в том числе с приусадебными участками), ...
... . В качестве средств разработки необходимо использование Borland C++ Builder 3.0 ClientServer, Microsoft Visual Basic for Applications. ГЛАВА 2. МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ СИСТЕМЫ ДОКУМЕНТООБОРОТА МИНТОРГА РФ. РЕШЕНИЕ ЗАДАЧ ИНФОРМАЦИОННОЙ БЕЗОПАСНОСТИ 2.1 Постановка задачи и её спецификация 2.1.1. Понятие информационной безопасности применительно к системе документооборота Минторга РФ Под ...
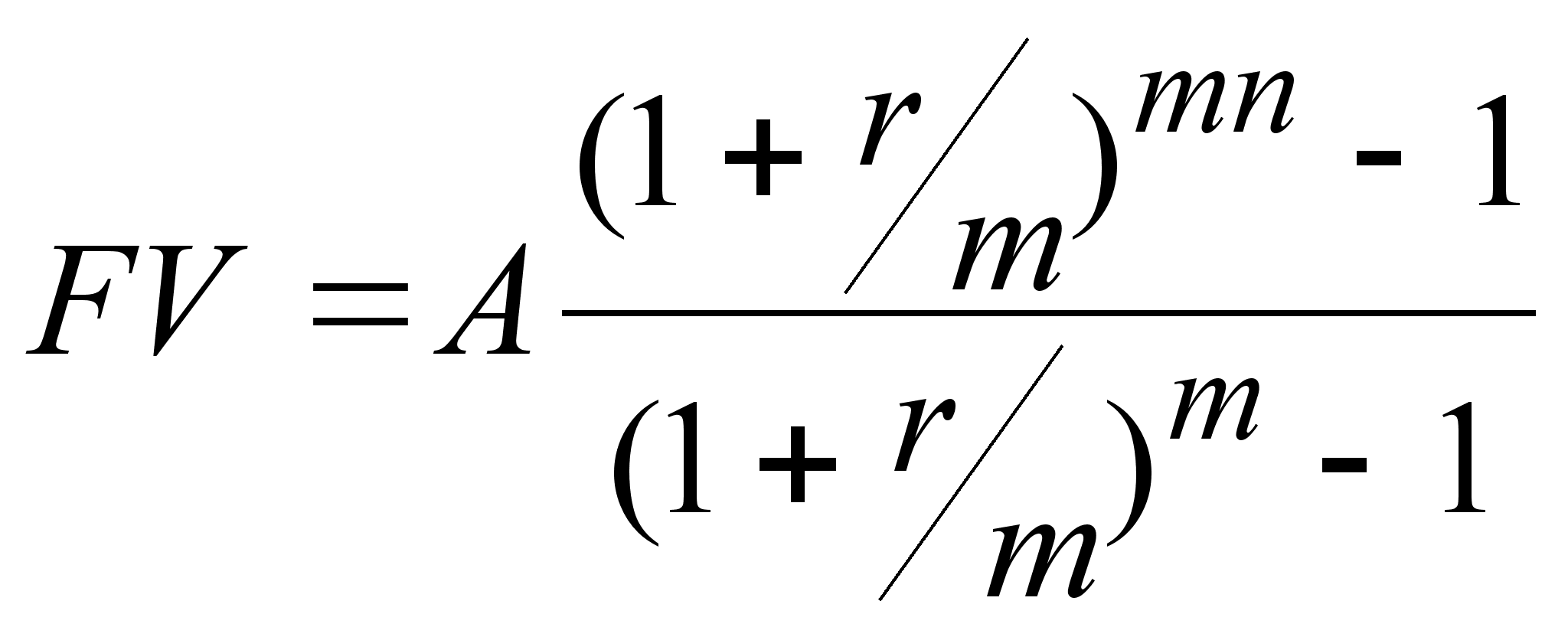
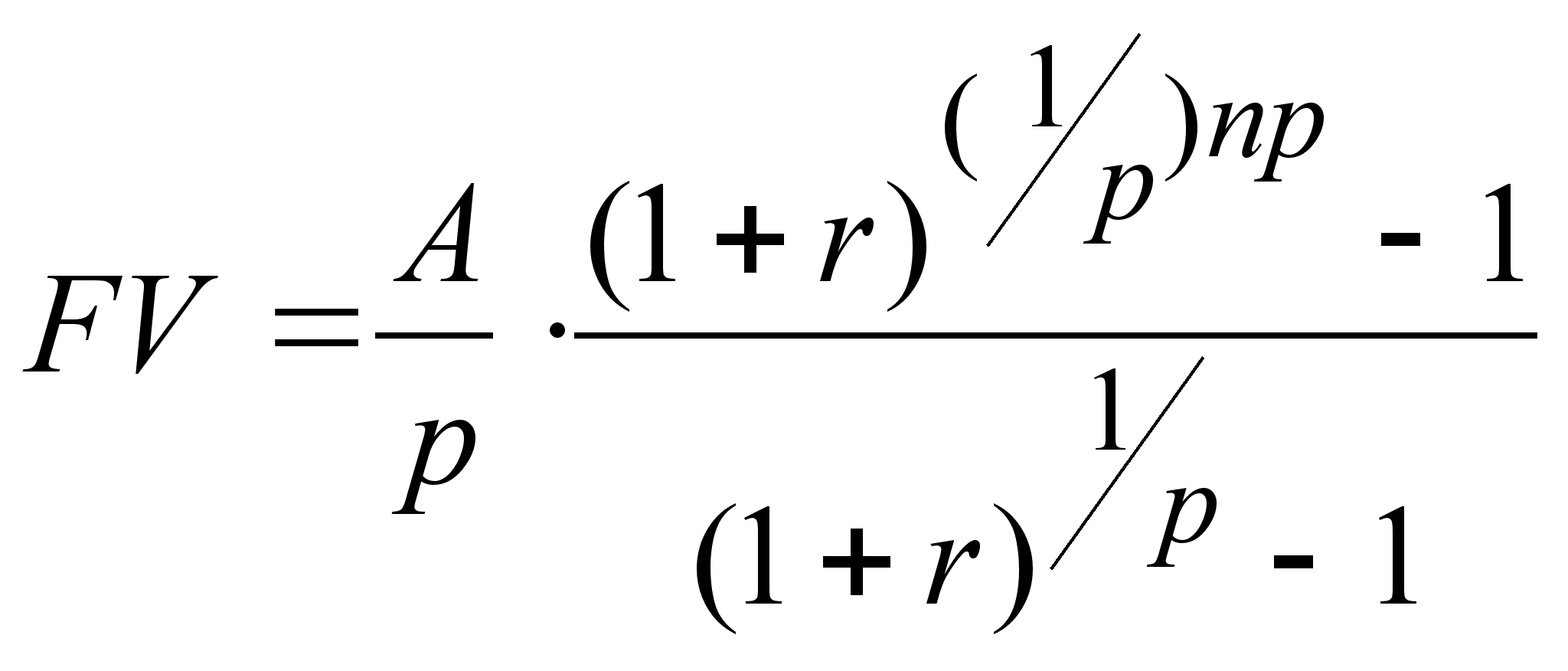
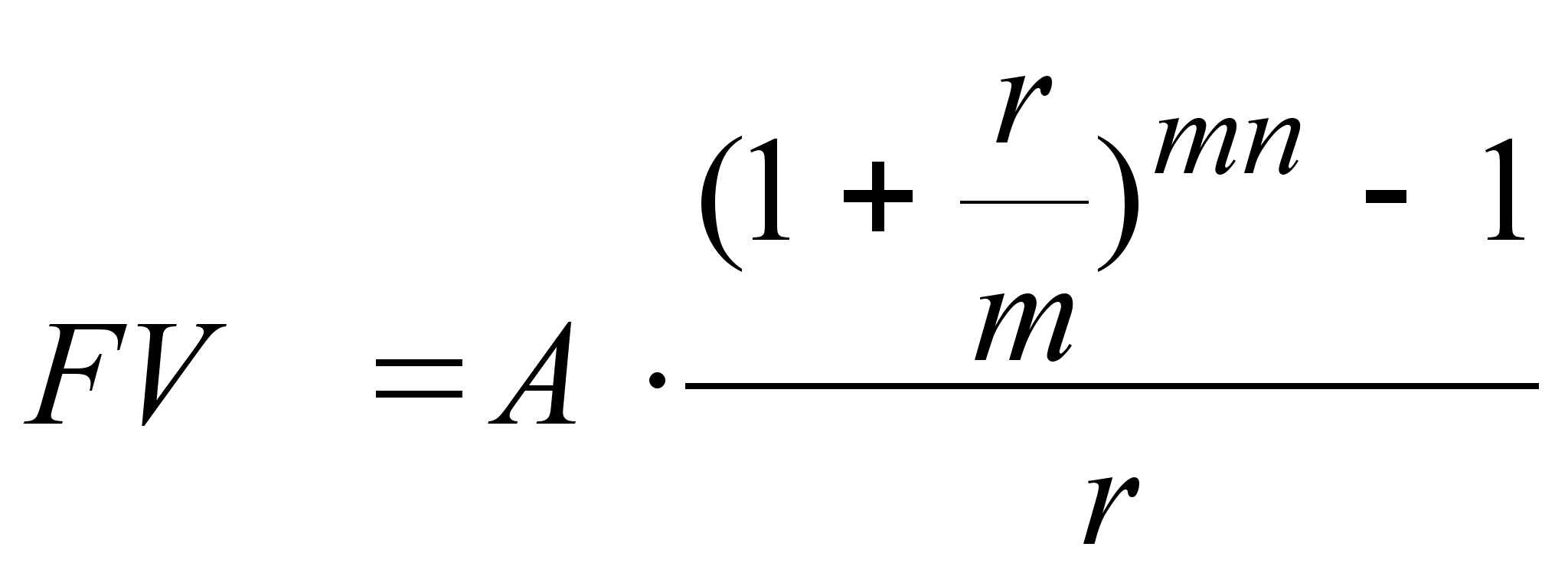
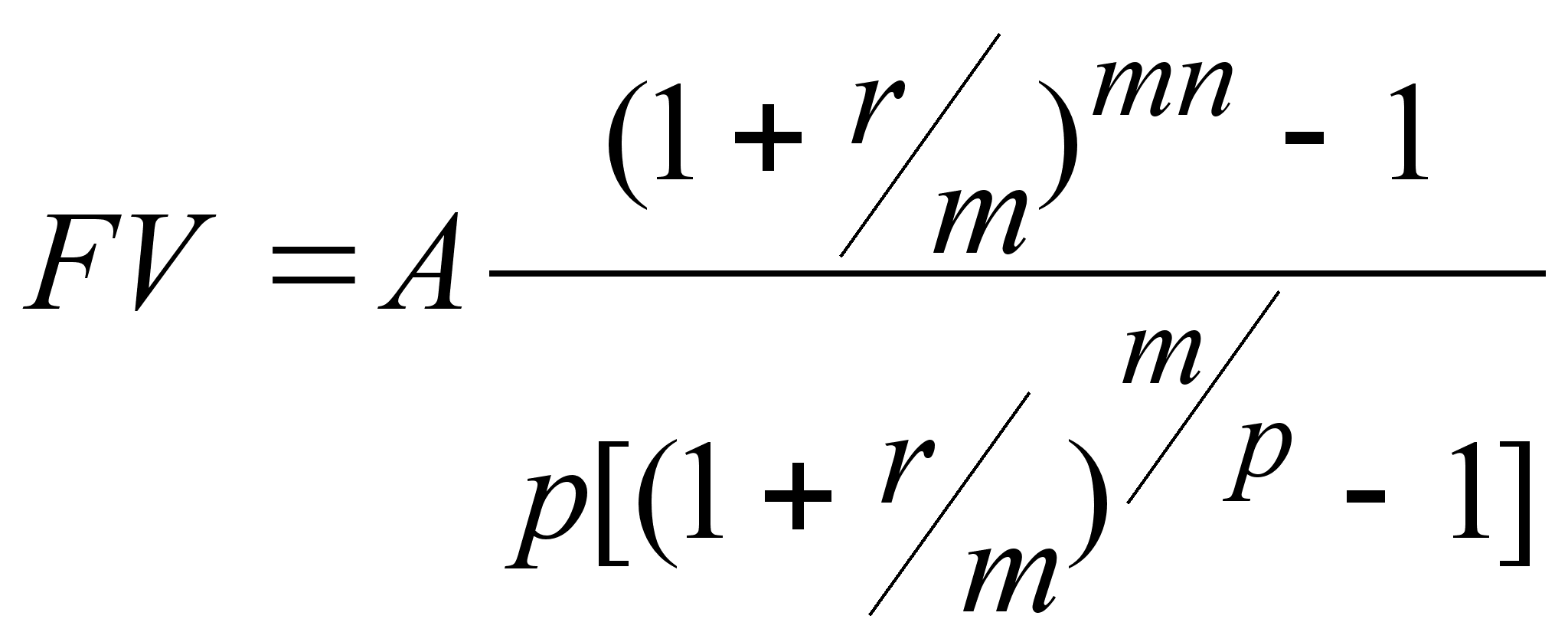
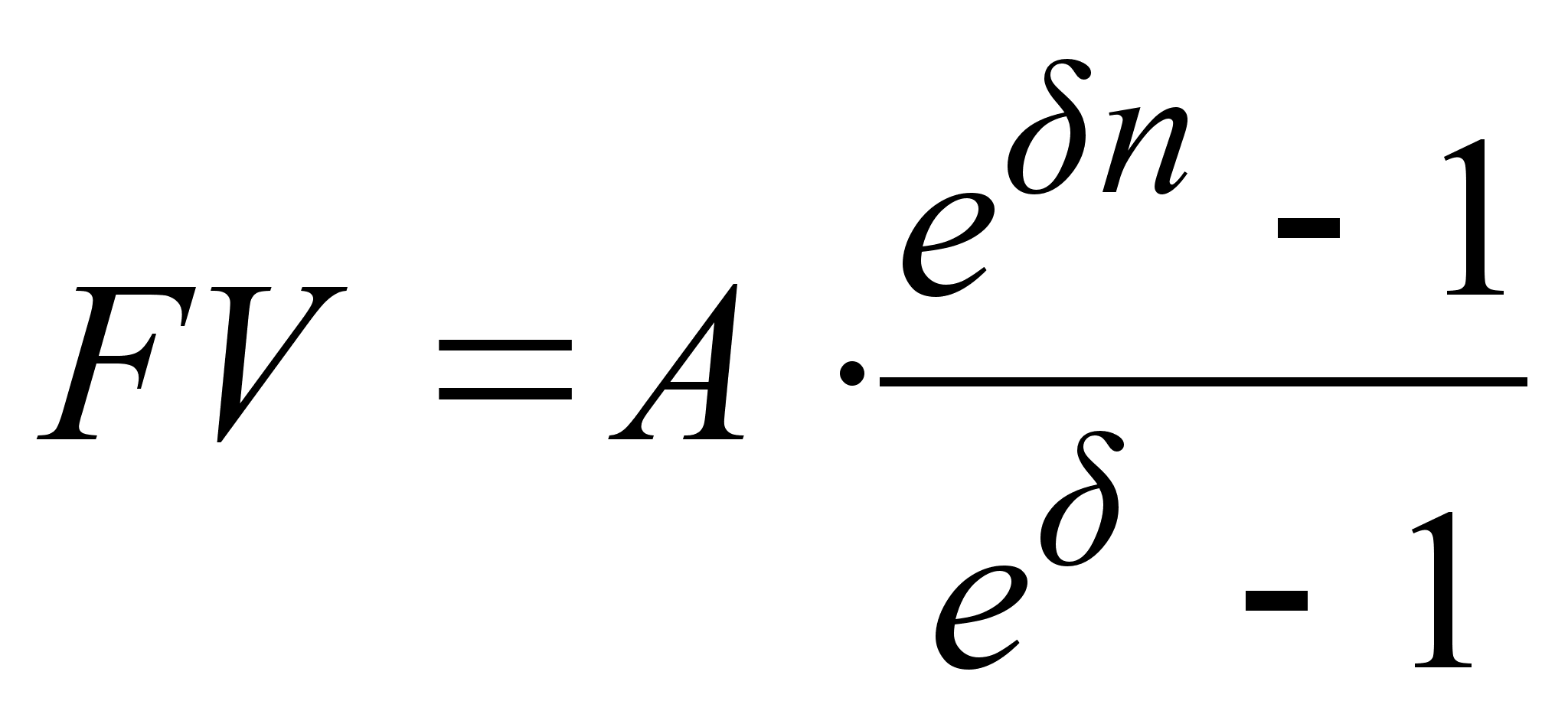
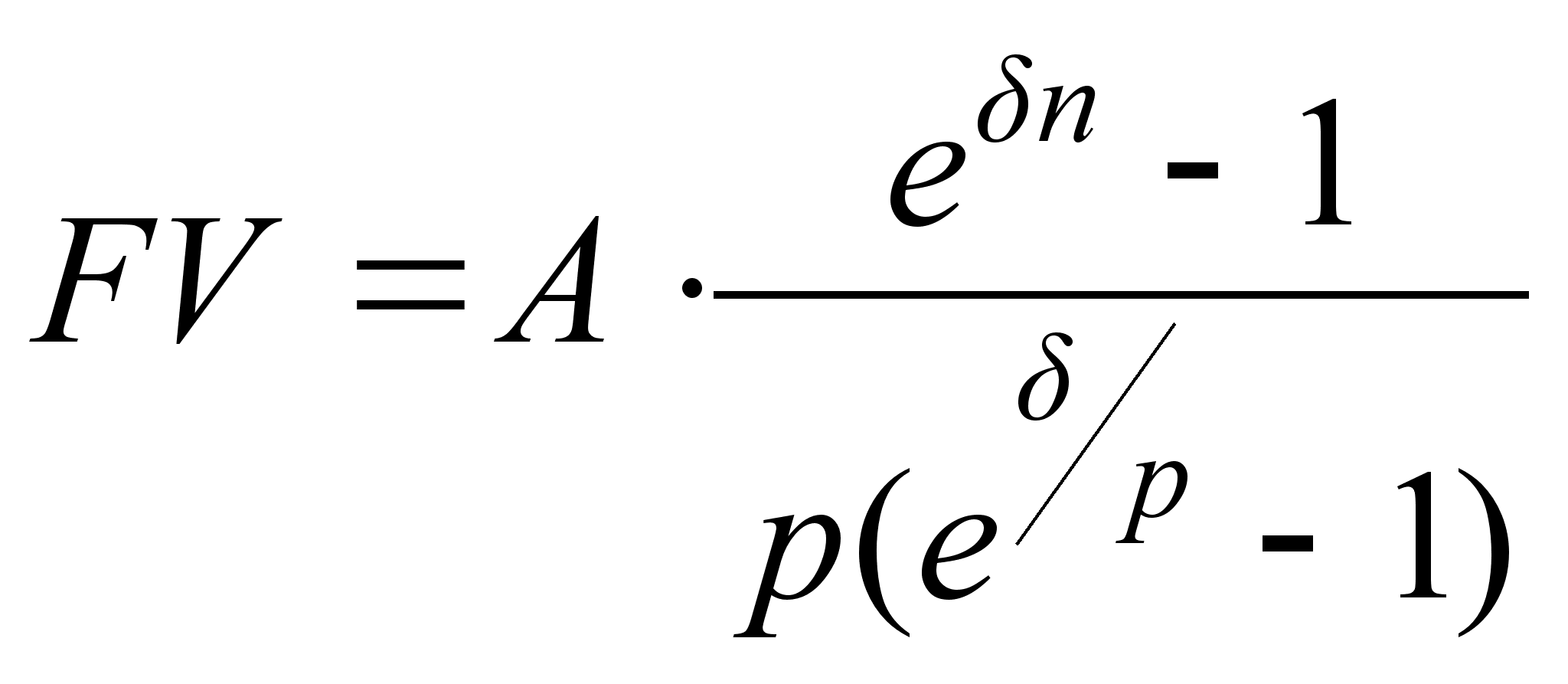
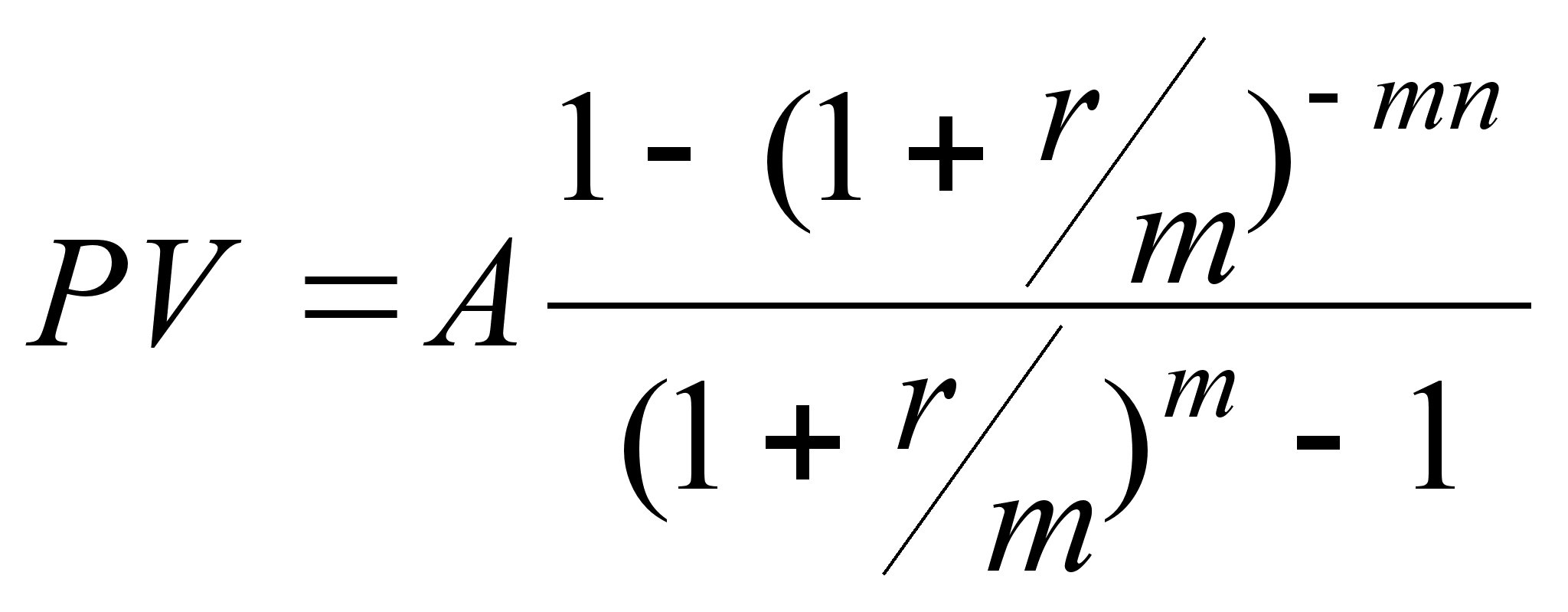
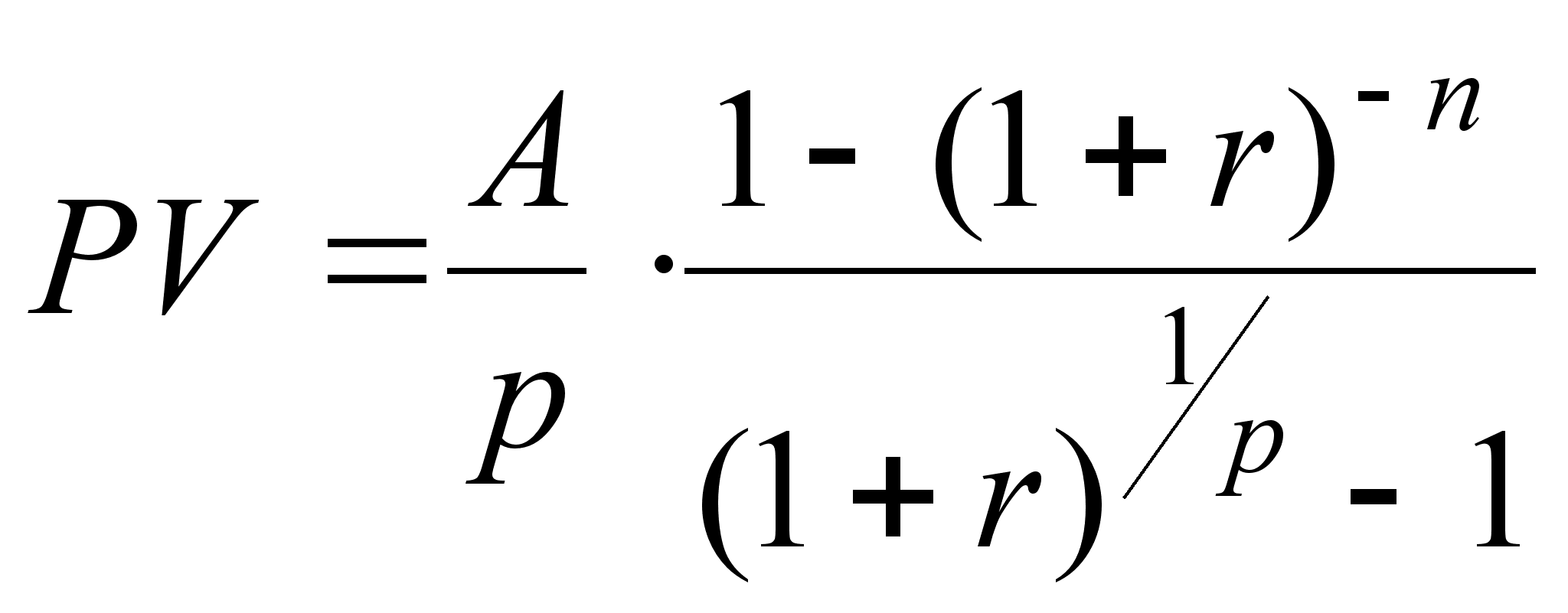
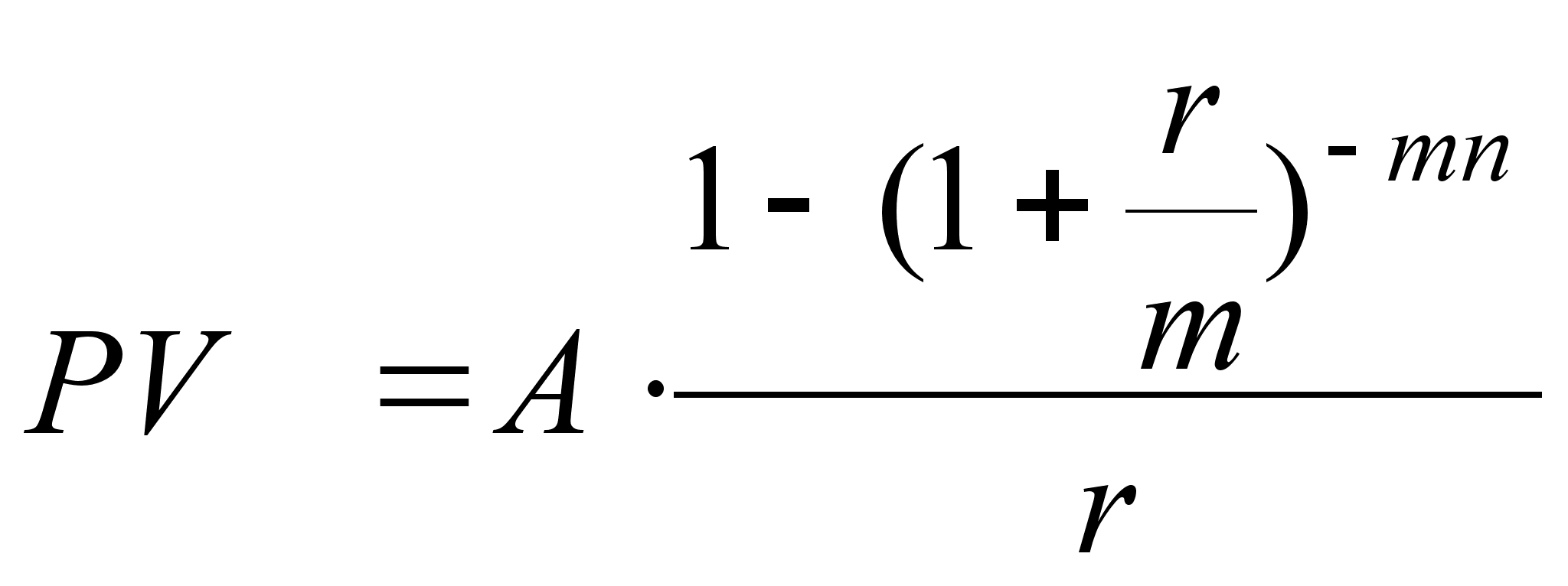
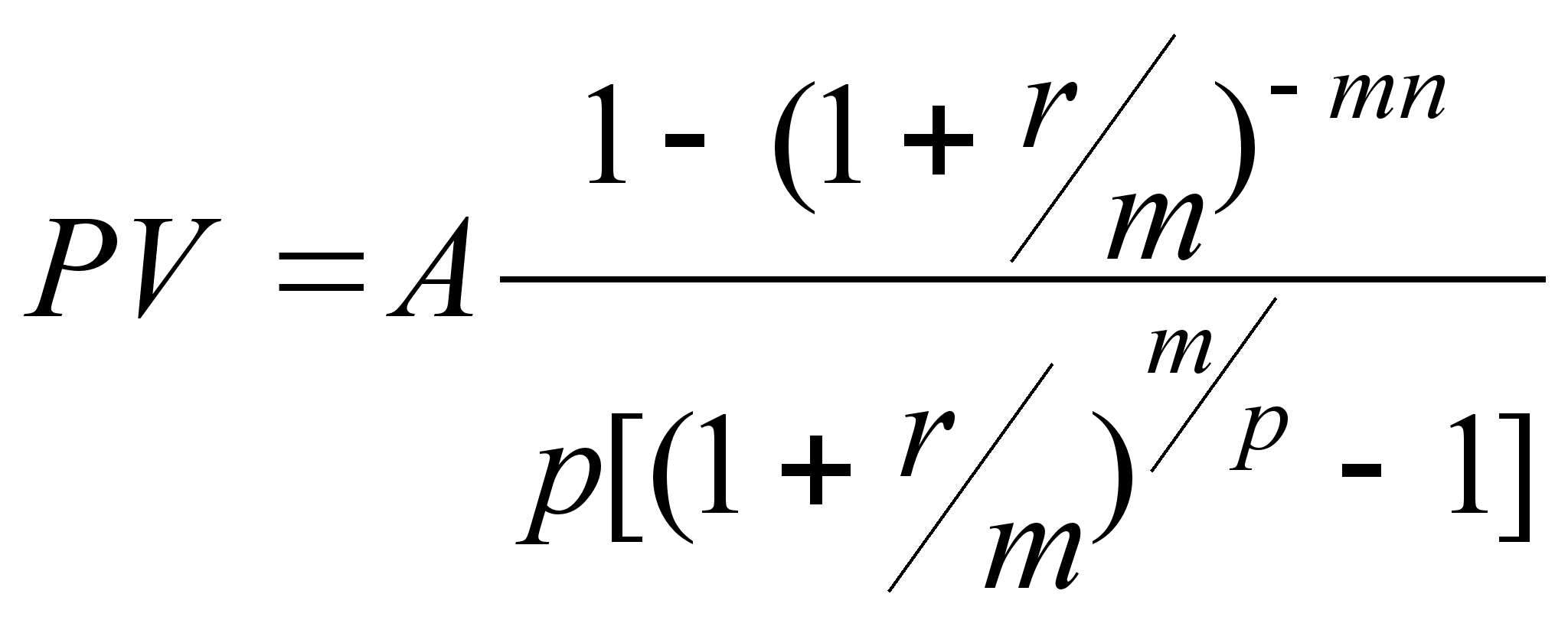
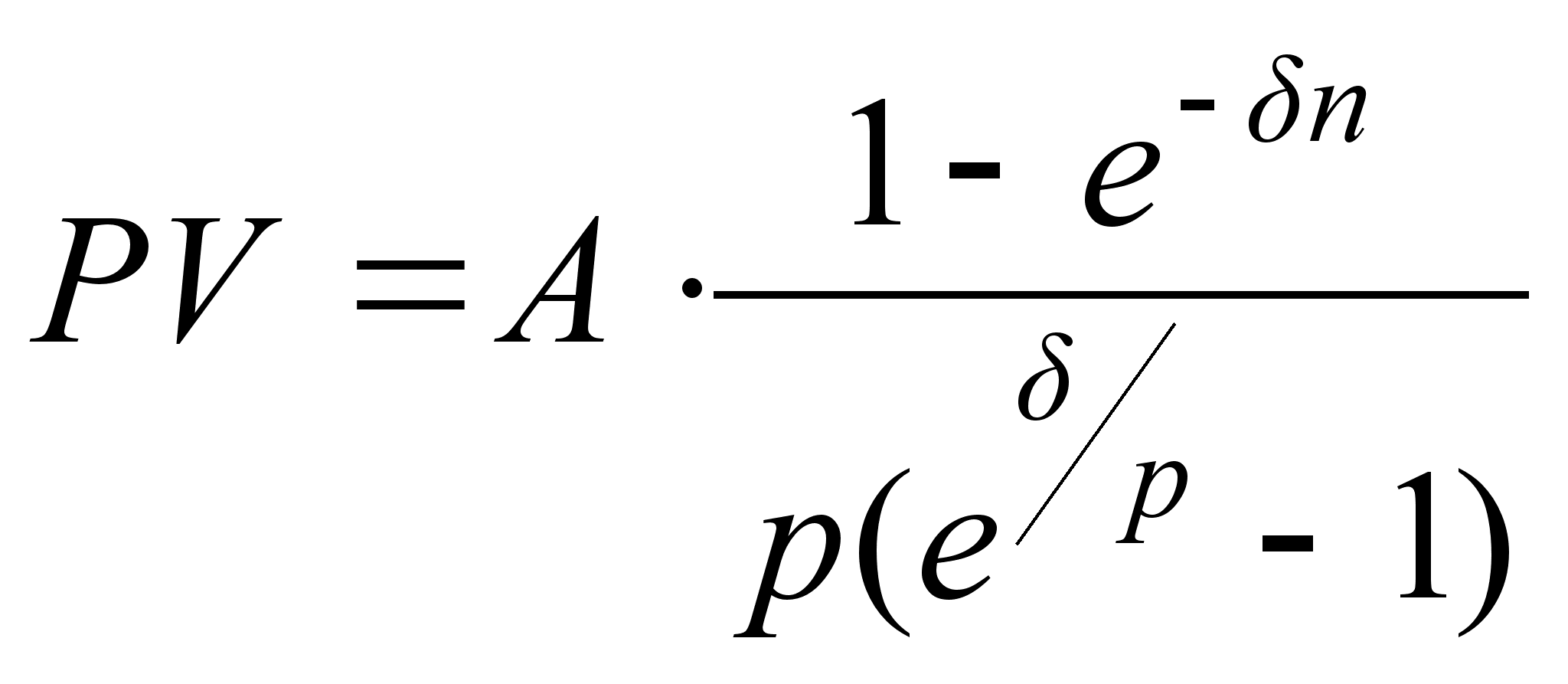

0 комментариев