Навигация
Условие уравнивания горизонта
2. Условие уравнивания горизонта.
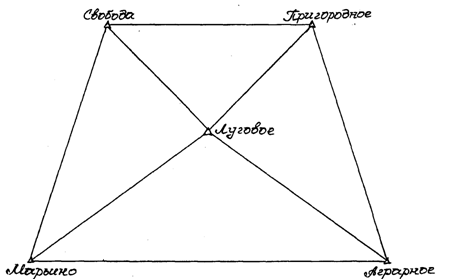
Сущность: в центральной системе при точке ТО сумма углов g должна быть равна 360°. Но практически будет невязка:
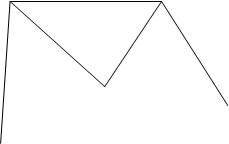
g4
![]() g5
g5

![]()
![]() g3
g3
 g1
g1
g2
![]()
а. g1+g2+g3+g4+g5-360°=¦g
поправка будет равна: ¦g/5
б. g1+(g1)+g2+(g2)+g3+(g3)+g4+(g4)+g5+(g5)-360° =0
Уравнение горизонта мы получим после вычитания формулы а. из б.
(g1)+(g2)+(g3)+(g4)+(g5)+¦g=0
Предельная невязка углов ¦ определяется формулой:
¦пред=2.5mbÖn
где n – количество углов при цетре.
3. Условное уравнение полюса:
Сущность: в каждом треугольнике должно быть выполнено условие пропорциональности сторон и противолежащих углов
bca/abc=1 это условие полюса в точке O для центральной системы.
Заменяя отношение сторон синусом противоположных углов, исправленных поправками. После логарифмирования и разложения функции в ряд мы получим:
W=lg(sin1sin3sin5/sin2sin4sin6)
Окончотельный вид полюсного условного уравнения будет выглядеть так:
d1(1)+d3(3)+d5(5)-d2(2)-d4(4)-d6(6)+W=0
Величина невязки зависит от ошибок в связующих углах
Wпред=2.5*mb*Ö(d)
4. Условное уравнивание сторон.
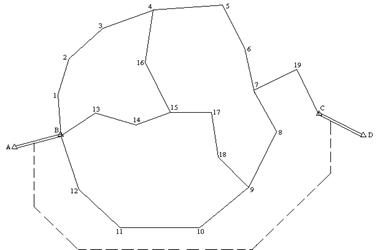
Условие сторон возникает в цепи треугольников расположенной между двумя сторонами исходной цепи. Геометрический смысл состоит в том, что при последовательном решении треугольников от начальной стороны должна быть получена конечная сторона.
d1(x1)+d2(x2)+d3(x3)+d4(x4)-b1(y1)-b2(y2)-b3(y3)-b4(y4)+WD=0
Wdпред=2.5*mb*Ö2mb+m2(d2+b2)
5. Условное уравнение координат
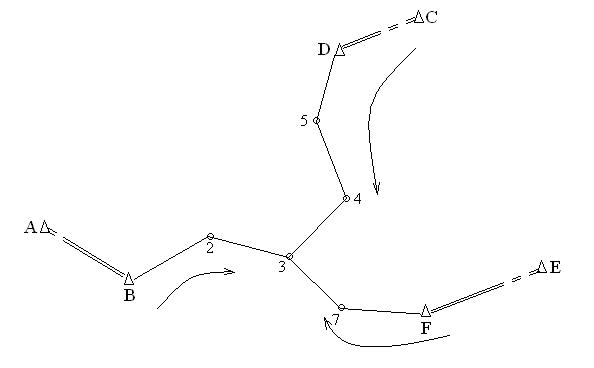
Условие координат возникает в сети, если в ней может быть выделен ход, заключенный между двумя твердыми точками.
Это условие заключается в том, чтобы сумма приращений по каждой координатной оси была равна разности координат конечной и начальной точек.
Невязки вычисляются по формуле:
¦x=åDx-(xк-xн); ¦y=åDy-(yк-yн)
сумма поправок приращений должна равнятся нулю.
dxBC+dxCD+dXDE+¦x=0
dyBC+dyCD+dyDE+¦=0
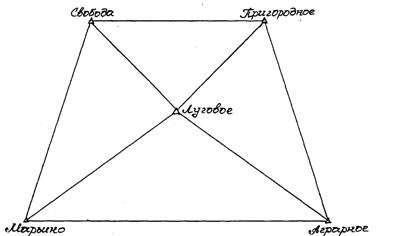
4. Упрощенное уравнивание центральной системы.
В центральной системе возникает условное уравнение фигур, горизонта и полюса. Математически эти условия выражаются уравнениями поправок. Число условных уравнений фигур равно числу треугольников:
(x1)+(y1)+f1=0
(x2)+(y2)+f2=0
(x3)+(y3)+f3=0
(x4)+(y4)+f4=0
(x5)+(y5)+f5=0
Одно условное уравнение горизонта имеет вид:
(g1)+(g2)+(g3)+(g4)+(g5)=fg=0
Условное уравнение полюса согласно формуле имеет вид:
d1(x1)+d2(x2)+d3(x3)+d4(x4)+d5(x5)- d1(y1)-d2(y2)-d3(y3)-d4(y4)-d5(y5)+W=0
Таким образом в этой центральной системе возникает семь условных уравнений. При этом распределение невязок и отыскание поправок по способу наименьших квадратов все уравнения надо решать совместно – это требует больших вычислений, поэтому в сетях сгущения уравновешивание выполняется упрощенным способом. Упрощение состоит в том, что система всех уравнений разделяется на однотипные группы. Для наиболее простого способа уравновешивания к первой группе относят условные уравнения фигур и решают их по способу наименьших квадратов. В этой группе уравнений каждоя неизвестная искомая поправка в уравнения входит один раз, т.е. каждое уравнение имеет три искомых неизвестных, не входящих в другие уравнения. Следовательно, каждое уравнение можна решать отдельно по способу наименьших квадратов. Решение такого уравнения с коэффициентами при неизвестных, равными единици, было описано.
Согласно формуле искомые поправки равны между собой и равны f/n, где f- невязки, а n- число углов.
Поэтому в условном уравнении фигуры треугольника n=3 поправки в углы треугольников выражаются формулами:
(x1)’=(y1)’=(g1)’=-f1 /3
(x2)’=(y2)’=(g2)’=-f2 /3
(x3)’=(y3)’=(g3)’=-f3 /3
(x4)’=(y4)’=(g4)’=-f4 /3
(x5)’=(y5)’=(g5)’=-f5 /3
Решение первой группы уравнений дает первичные поправки, обозначенные одним штрихом. Затем приступают к решению второй группы условных уравнений, т.е. уравнение горизонта. При упрощенном уравновешивании получают вторые поправки к углам.
Условное уравнение примет вид:
(g1)”+ (g2)”+ (g3)”+ (g4)”+(g5)”+fg=0
Здесь невязка вычисляется по первично исправленным углам, т.е.
fg=[g1+(g1)’]+ [g2+(g2)’]+ [g3+(g3)’]+ [g4+(g4)’]+ [g5+(g5)’]-360°
Условное уравнение горизонта имеет коэффициенты при неизвестном, равные единице, поэтому решение уравнения по способу наименьших квадратов выполняются так же, как и условие фигур, невязка распределяется поровну на все углы и поправка равна -fg /n, следовательно, вторичные поправки к углу g будут:
(g1)”= (g2)”= (g3)”= (g4)”= (g5)”-fg” /n
Чтобы не нарушать условие фигур, выполненные введением первых поправок, надо и в связующие углы x, y каждого треугольника ввести вторичные поправки, которые должны быть равны половине второй поправки к углу g с обратным знаком:
(x1)”=(y1)”=-(g1)”/2
(x2)”=(y2)”=-(g2)”/2
Результаты этих поправок записаны в таблице. После решения условных уравнений фигур и горизонта приступают к решению полюсного условного уравнения, что дает третьи поправки к углам, но при условии, чтобы условия фигур и горизонта не были нарушены. Условное уравнение полюса примет вид:
d1(x1)”’+d2(x2)”’+d3(x3)”’+d4(x4)”’+d5(x5)”’-d1(x1)”’- d1(x1)”’-d1(x1)”’-d1(x1)”’ --d1(x1)”’+W=0
здесь d1, d2, …d5 – перемена логарифмов синусов углов x, входящие в числитель свободного члена W, а b1, b2…b5 – перемены логарифмов синусов углов y, входящие в знаменатель свободного члена. Невязка, т.е. свободный член уравнения, выражается формулой:
Здесь связующие углы x, y каждого треугольника представляют углы, исправленные предыдущими двумя поправками. Чтобы решением полюсного уравнения не нарушить условие фигур и горизонта, надо ввести дополнительное условие, согласно которому в каждом треугольнике связующие углы должны иметь равные поправки, но с разными знаками, т.е. (xi)”’=-(yi)”’. Тогда полюсное уравнения примет вид.
a1(x1)”’+ a2(x2)”’+ a3(x3)”’+ a4(x4)”’+ a5(x5)”’+W=0
a1=(d1+b1), …
для решения этого уравнения по способу наименьших квадратов надо добавить условие: (x1)”’2+(x2)”’2+(x3)”’2+(x4)”’2+(x5)”’2=min
для нахождения минимума функции возьмем производные и прировняем их к нулю.
f’x1=2(x1)”’-2ka1=0
f’x2=2(x2)”’-2ka2=0
………………………
f’xi=2(xi)”’-2kai=0
откуда поправки:
(x1)”’=a1k
(x2)”’=a2k
…………………….
(xi)”’=aik
подставляем полученные (x) в формулу
a1a1k+ a2a2k+ a3a3k+ a4a4k+ a5a5k+W=0
или
[aa]k+W=0
откуда
k=-W/[aa]
после обработанной замены коэффициента ai=dI+bi формула кореллатты k примет вид:
k=-W/å(d+b)2
Значение k начисляют по записям. После подстановки значения k в формулу поправок получим:
Эти поправки записывают в таблицу. После исправления углов третьими поправками решают треугольники на основе исходной стороны, т.е. находят длины сторон, затем вычисляют дирекционные углы сторон от дирекционного угла начальной линии. После вычисления дирекционных углов и длин линий вычислений приращения. В сомкнутом полигоне центральной системы будут невязки приращений fx , fy, которые распределяют пропорционально длинам линий. Так как в треугольниках сети сгущения длины сторон не очень отличаются между собой, то невязки приращений можно распределять поровну. После исправления приращений вычисляют координаты пунктов.
РАЗДЕЛ IV
Охрана труду в землеустройстве.
Техника безопасности при выполнении работ по землеустройству
Землеустройство включает проектно- изыскательские, съемочные и обследовательские работы.
Поскольку работу выполняют под открытым небом, возможен перегрев и переохлаждение организма, а следовательно, возможны солнечные удары, простудные и ревматические заболевания.
При съемочных и обследовательских работах возможны укусы насекомых и змей.
К работе по землеустройству допускаются лица, прошедшие медосмотр и получившие вводный инструктаж на рабочем месте по технике безопасности. В нужных случаях назначаемые на выполнение полевых работ проходят вакцинацию и обеспечиваются соответствующими средствами безопасности и защиты: спецодеждой, спец обувью, очками и т. д.
Рабочий обязан следить за исправленностью и чистотой спецодежды и других средств защиты. Запрещается стирать спецодежду в легковоспламеняющихся жидкостях.
Все работники должны строго соблюдать трудовую и производственную дисциплину. Запрещается без разрешения руководителя работ отлучаться с места работы и из полевого лагеря.
При организации полевого лагеря, палатки нужно устанавливать вне пределов возможного затопления и падения сухостойных деревьев, камней, осыпей. Территорию лагеря очищают устраняя мешающие проходу предметы.
При движении по лесу следуют поддерживать зрительную и голосовую связь в движущиеся группы.
Во избежании травмирования ветками необходимо между идущими выдерживать расстояние не менее 3 м.
Когда работы проводят в безводных местах, люди должны знать, где расположены колодцы и водоемы, иметь термос с кипяченой водой.
В случае обследования земель в заболоченной местности передвигаются по целине болот нужно « след в след » с интервалами между идущими 2 – 3 м с применением шестов, веревок.
Кочковатые болота безопаснее переходить по кочкам со страховочным шестом.
Переезды на транспортных средствах разрешаются, если эти средства приспособлены для перевозки людей.
Во время выполнения работ необходимо строго подходить к питанию и к поддержанию питьевого режима.
Продукты следует хранить в упаковке.
Питьевая вода должна быть чистой, кипяченой.
Купаться можно в предварительно проверенных местах. Запрещается выходить на полевые работы без карты, компаса, медицинской аптечки, лопаты и топора.
РАЗДЕЛ VТЭР.
РАЗДЕЛ VIСписок литературы.
ПРИЛОЖЕНИЕПохожие работы
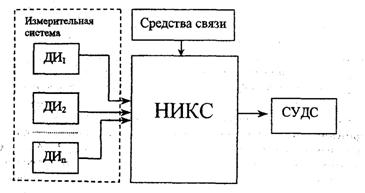
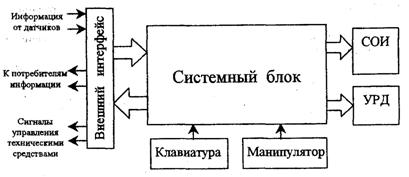
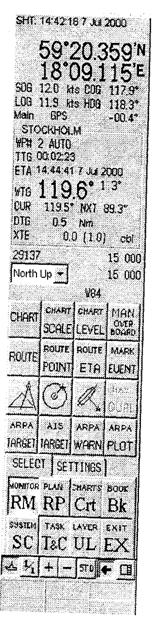
... информации. Набираемая информация отображается на дисплее, что позволяет контролировать ее правильность. Клавиатура и дисплей АИС должны быть независимыми от других навигационных устройств. Судовыми системами отображения АИС могут быть система отображения электронных карт (ECDIS, ECS, RCDS), РЛС, САРП или дисплей персонального компьютера. АИС и связанные с ней датчики информации питаются от ...
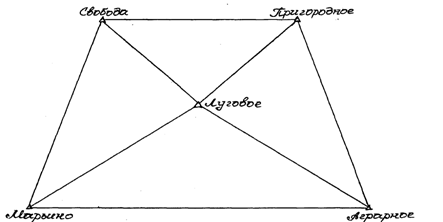
... 1 5008,50 1000,00 1753,45 2748,03 2376,28 72 º28'50'' 101 º12'25'' 351 º18'32'' Луговое Аграрное Свобода 2. Уравновешивание систем ходов плановой съемочной сети 2.1 Уравновешивание систем теодолитных ходов с одной узловой точкой 2.1.1 Задание Произвести уравновешивание систем теодолитных ходов, сходящихся в узловой точке 3 и опирающихся ...
0 комментариев