Навигация
Topic: Is Collusion Possible?
2 group.
Teacher: Alla Friedman.
Международный Институт Экономики и Финансов, 3 курс.
Высшая Школа Экономики
Essay in Microeconomics.
Topic:
Is Collusion Possible?
18.12.2000
Contents:
1. Introduction.
2. Two types of behaviour (Collusive and non-collusive).
3. Game theory.
a.) Concept.
b.) The problem of collusion.
c.) Predatory pricing.
4. Repeated games approach.
a.) Concept.
b.) Finite game case.
c.) Infinite game case.
i.) “Trigger” strategy
ii.) Tit-for-Tat.
d.) Finite game case, Kreps approach.
5. The motives for retaliation.
6. Conclusion.
7. Bibliography.
1. Introduction.
In this essay I would discuss the price and output determination under the one essential type of imperfect competition markets- oligopoly. Inter-firm interactions in imperfect markets take many forms. Oligopoly theory, those name refers to “competition among the few”, lack unambiguous results of these interactions unlike monopoly and perfect competition. There is a variety of results derived from many different behavioural assumptions, with each specific model potentially relevant to certain real-world situations, but not to others.
Here we are interested in the strategic nature of competition between firms. “Strategic” means the dependence of each person’s proper choice of action on what he expects the other to do. A strategic move of a person influences the other person’s choice, the other person’s expectation of how would this particular person behave, in order to produce the favourable outcome for him.
2. Two types of behaviour (Collusive and non-collusive).
Models of enterprise decision making in oligopoly derive their special features from the fact that firms in an oligopolistic industry are interdependent and this is realised by these firms. When there are only a few producers, the reaction of rivals should be taken into account. There are two broad approaches to this problem.First, oligopolists may be thought of as agreeing to co-operate in setting price and quantity. This would be the Collusive model. According to this model, firms agree to act together in their price and quantity decisions and this would to exactly the same outcome as would have been under monopoly. Thus the explicit or co-operative collusion or Cartel would take place.
Second approach of the oligopoly analysis is based on the assumption that firms do not co-operate, but make their decisions on the basis of guesses, expectations, about the variables to which their competitors are reaching and about the form and the nature of the reactions in question. The Non-collusive behaviour deals with this model. Here, though in equilibrium the expectations of each firm about the reactions of rivals are realised, the parties never actually communicate directly with each other about their likely reactions. The extreme case of this can even imply competitive behaviour. Such a situation is much less profitable for firms than the one in which they share the monopolistic profit. The purpose of this paper is to analyse the case of the possibility of collusion between firms in order to reach the monopolistic profits for the industry, assuming that they do not co-operate with each other. This would be the most interesting and ambiguous case to look at.
3. Game theory.
a.) Concept.
The notion of game theory would a good starting point in the study of strategic competition and would be very helpful in realising the model and the problems facing oligopolistic firms associated with it.
Game theory provides a framework for analysing situations on which there is interdependence between agents in the sense that the decisions of one agent affect the other agents. This theory was developed by von Neumann and Morgenstern and describes the situation, which is rather like that found in the children’s game “Scissors&Stones”. Each firm is trying to second-guess the others, i.e. the behaviour of one firm depends on what it expects the others to do, and the in turn are making their decisions based upon their expectations of what the rivals (including the first firm) will do. In our case, the players of the game are the firms in the industry and each of them wants to maximise its pay-off. The pay-off that a player receives measures how well he achieves his objective. Let’s assume in our model the pay-off to be a profit. Their profits depend upon the decisions they make (the strategies chosen by the various players including themselves). A strategy in this model is a plan of action, or a complete contingency plan, which specifies what the player will do in any of the circumstances in which he might find himself. The game also depends on the move order and the information conditions.
Games can be categorised according to the degree of harmony or disharmony between the players’ interests. The pure coordination game is the one extreme, in which players have the same objectives. The other extreme is the pure conflict of the opposite interests of players. And usually there is a mixture of coordination and conflict of interests- mixed motive games.
Although the importance of the other players’ choices takes place, sometimes a player has a strategy that is the best irrespective of what others do. This strategy is called dominant, and the other inferior ones are called dominated. A situation in which each player is choosing the best strategy available to him, given the strategies chosen by others, is called a Nash equilibrium. This equilibrium corresponds to the idea of self-fulfilled expectations, tacit, self-supporting agreement. If the players have somehow reached Nash equilibrium, then none would have an incentive to depart from this agreement. Any agreement that is not a Nash equilibrium would require some enforcement.
b.) The problem of collusion.
Now I would like to use an example of a game in which the Cournot output deciding duopoly is involved. This game is illustrated by the table below:
| Firm B’s output level | |||
| HIGH | LOW | ||
| Firm A’s output level | HIGH | (1;1) | (3;0) |
| LOW | (0;3) | (2;2) | |
Here a firm chooses between two alternatives: high and low output strategies. The corresponding pay-offs (profits) are given in the boxes. In this game, the best thing that can happen for a firm is to produce a high level of output while its rival produces low. Low output of the rival provides that price is not driven down too much, thus a firm could earn a good profit margin. The worst thing for a firm is to change places with its rival assuming the same situation takes place. If both firms produce high levels of output, then the price would be low, allowing each of them to earn still positive but very small profits. Nevertheless, (HIGH;HIGH) would be the dominant strategy of this game (we would observe a Nash equilibrium in strictly dominant strategies here). It is the best response of firm A whenever B produces a high or low output and this is also true for firm B. The non-co-operative outcome for each firm would be to get the pay-off of 1. But as we can see, it would be better for both to lower their output and thereby to raise price, as their profits would increase to 2 for each firm instead of 1 in NE. Strategy (LOW;LOW) would be the collusive outcome. The problem of collusion is for the firms to achieve this superior outcome notwithstanding the seemingly compelling argument that high output levels will be chosen.
This was an example of a “one-shot” game and we saw that the collusive outcome was not available for that case. But in reality these games are being played over and over (on a long-term basis) and we will see later in this essay how the collusion can be sustained by threats of retaliation against non-co-operative behaviour.
c.) Predatory pricing.
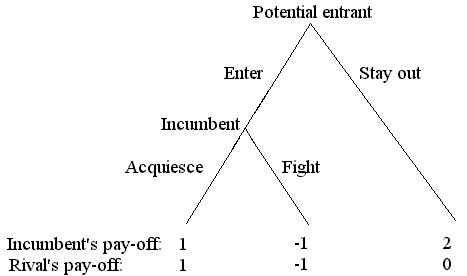 |
Here we need to introduce the explicit order of moves in the model. There are again two players-firms on the market- an incumbent firm and a potential entrant in the market. The game is illustrated below:
The potential entrant chooses between entering and staying out of the industry. In the case of his entering, the incumbent firm can either fight this entry (which as we see would be costly to both), or acquiesce and arrive at some peaceful co-existence (which is obviously more profitable). The best thing for incumbent is for entry not to take place at all. There are in fact two Nash equilibria: (IN;ACQUIESCE) and (OUT;FIGHT). But the last mentioned (OUT;FIGHT) is implausible, as if the incumbent were faced with the fact of entry, it would more profitable for him to acquiesce rather than to fight the entry. Due to this fact the potential entrant would choose to enter the industry and the only equilibrium would be (IN;ACQUIESCE). Thus we can conclude, that in this case the incumbent’s threat to fight was empty threat that wouldn’t be believed, i.e. that threat was not a credible one. The concept of perfect equilibrium, developed by Selten (1965;1975), requires that the “strategies chosen by the players be a Nash equilibrium, not only in the game as a whole, but also in every subgame of the game”. (In our model on the picture, the subgame starts with the word “incumbent”). We have got the perfect equilibrium to rule out the undesirable one.
Похожие работы
... agencies, mass media, narcological centers, and social services. The research component aims to define and analyze data on drug abuse, to work out recommendations for overcoming it, to set up and run special research labs, and to find new ways of ending drug addiction. The technical component includes identifying drugs, designing equipment for special labs, developing remote control devices to ...
... «Bloody Child» represents Macduff, who was «from his mother’s womb untimely ripped». These ingenlities might well have been intrusive in a play so elemental; as haundled by Shakespeare they contribute to the master plan by allowing us to watch Macbeth gradually stripped of hope by those juggling fiends» upon whom he has relied. Such lines us Hecate: O, well done! I commend your pains And ...
... on the subject. This absence of evidence is then replaced by ridiculing the subject through association with other 'fringe' topics; so-called experts are brought-in to explain away all the events as freak weather conditions or the work, general pranksters, even sexually excited animals! According to TV documentaries, all crop circles up to 1992 were made by two simple, elderly men called Doug ...
0 комментариев