Определение глубины предпрогнозной ретроспекции с учетом старения информации

4.4. Определение глубины предпрогнозной ретроспекции с учетом старения информации

Наиболее общая постановка задачи сравнения результатов прогнозных расчетов, полученных с использованием различной глубины ретроспекции, заключается в следующем. С целью выявления периода старения информации определяется k значений глубины ретроспекции (Т₂, Т₃, …, Т_k+1). Значение Т₁=0 целесообразно принять за контрольную точку, так как вполне очевидно, что в этой точке информация еще не устарела и ее можно считать наиболее ценной и достоверной. В ходе прогнозных исследований определяется … значений точечных оценок прогноза X_j(T_j). Если ввести в рассмотрение разность точечных оценок

Z₁=X₂(T₂)-X₁(T₁), Z₂=X₃(T₃)-X₃(T₂),…,Z_j=
=X_j+1(T_j+1)-X_j(T_j),…Z_k=X_k+1(T_k+1)-X_k(T_k), (2.27)

то значения Z_j(j=1, …, k) можно считать независимыми случайными величинами, поведение которых описывается некоторым неизвестным законом распределения F(Z).

Ограниченный объем используемой информации не позво­ляет достаточно надежно его определить методами математи­ческой статистики. Поэтому требуется разработка специальных методов решения задачи сравнения результатов прогнозов по ограниченному набору ретроспекций.

Следует заметить, что выборочные моменты (математиче­ское ожидание, дисперсия и др.) могут быть определены по вы­борке Z_j(j=1, …, k).

Определение закона распределения случайной величины Z и его анализ позволяют дать статистическую и смысловую интер­претацию результатов сравнения прогнозных исследований, оп­ределить коэффициент доверия (или построить доверительную область), проверить статистическую гипотезу о непротиворечи­вости данных прогноза и контрольного значения динамического ряда.

Традиционно для описания подобного рода случайных ве­личин обращаются прежде всего к нормальному (гауссовскому) распределению, которое играет фундаментальную роль в вероятностно-статистических исследованиях.

Традиционная универсальность нормального закона, как было отмечено выше, объясняется, прежде всего, полнотой теоретических исследований, относящихся к нему. При са­мых широких предположениях суммы случайных величин ведут себя асимптотически нормально (соответствующие ус­ловия и составляют содержание так называемой предельной теоремы). Во многих случайных величинах можно видеть суммарный аддитивный эффект большого числа независимых причин и т.д. В силу изложенных обстоятельств этот закон распределения широко используется в качестве модели для различных статистических совокупностей. В тех случаях, ко­гда гипотеза о принадлежности статистической совокуп­ности генеральной нормальной совокупности не под­тверждается опытными данными или когда теорети­ко-вероятностная схематизация вероятностного эксперимента порождает другую модель, представляется целесообраз­ным в силу универсальности нормального закона обра­титься к теории суммирования случайного числа нормаль­ных случайных величин.

Теоретической основой процедуры уточнения математиче­ской модели формирования закона распределения случайной величины Z является аппарат характеристических функций.

В этом случае функция распределения F(Z) суммы случай­ного числа n случайных величин Z, на основании мультиплика­тивного свойства характеристических функций определяется характеристической функцией

(2.28)

где характеристическая функция нормальной слу­чайной величины с параметрами m и a.

В качестве примера, имеющего прикладное значение в рас­сматриваемой области, рассмотрим распределение суммы пуассоновского числа нормально распределенных случайных вели­чин. С этой целью составим уравнение

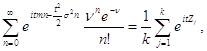(2.29)

правая часть которого равна эмпирической характеристиче­ской функции. Параметры нормального закона распределения m и a и закона Пуассона v могут быть определены в результате минимизации невязки или с помощью моментов. Метод момен­тов применительно к рассматриваемому уравнению заключа­ется в приравнивании некоторого количества выборочных моментов, оцениваемых по правой части уравнения (2.29), к со­ответствующим теоретическим, определяемым по характери­стической функции левой части уравнения в соответствии с за­висимостью

(2.30)

Естественно, что число получаемых в этом случае уравне­ний должно быть равным числу оцениваемых параметров (в данном случае трем).

Последовательно дифференцируя характеристические функции по t и приравнивая в полученных производных значе­ния t нулю, можно составить следующую систему уравнений

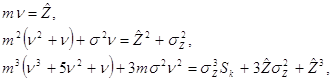(2.31)

где S_k-асимметрия закона распределения, равная центральному моменту третьего порядка.

После некоторых алгебраических преобразований из систе­мы уравнений (2.31) можно определить среднее число сумми­руемых случайных величин (параметр закона Пуассона).

(2.32)

математическое ожидание и среднеквадратическое отклонение суммируемой нормальной случайной величины

 и (2.33)

В формулах (2.32) и (2.33) коэффициент вариации V_z опре­деляется по первым двум моментам  и

Используя формулу обращения

можно получить плотность распределения пуассоновского чис­ла нормальных случайных величин

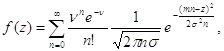(2.34)

Очевидно, что плотность распределения (2.34), а точнее па­раметры v, m и s, зависят от объема выборок случайных вели­чин {Z_j}, j=1,…,k; j=1, k=1, k-1 и т.д. Последовательно от этапа к этапу анализируя ретроспективную информацию, можно построить семейство плотностей распределения f_j(z) (j=k, k-1, …). Задачу отбраковки устаревшей информации в этом случае сводится к решению последовательного ряда задач проверки статистических гипотез о принадлежности контрольного значе­ния параметра Z₀ генеральной совокупности, описываемой за­коном распределения с плотностью (2.34). При этом следует учесть, что в силу проведенной схематизации процесса Z₀=0. Тогда, задаваясь уровнем значимости a и учитывая симметрич­ный характер закона распределения (2.34), можно найти такое значение индекса j, при котором выполнилось бы одно из сле­дующих неравенств

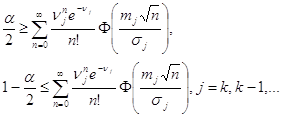(2.35)

где 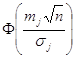 – функция Лапласа.

Справедливость соотношений (2.35) вытекает из очевидной процедуры вычисления функции распределения через плотность (2.34)

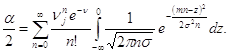(2.36)

Таким образом, задача определения глубины предпрогнозной ретроспекции с учетом старения информации может быть достаточно надежно решена традиционными методами матема­тической статистики с помощью математической модели (рас­пределения сумм пуассоновского числа нормально распреде­ленных случайных величин).

ЗАКЛЮЧЕНИЕ

В данной курсовой работе рассмотрены основные методы прогнозирования экономической среды с учетом фактора старения информации на примере рыночного механизма спрос-предложение.

Проанализировав полученную информацию, можно сделать выводы о том, что для различных наук, отраслей, экономических сфер старение информации понятие растяжимое. Для одних информация, полученная десять лет назад, все еще представляется важной, а для других, неважной является информация, полученная в течении последних суток.

Также для различных отраслей применяют различные методы учета фактора старения информации. С помощью таких методов можно из имеющейся в наличии информации для прогнозирования выжать максимум полезной информации.

Список литературы

1.   Б.П Ивченко, Л.А. Мартыщенко, И.Б. Иванцов. «Информационная микроэкономика». Часть 1. Методы анализа и прогнозирования, СПб.: «Нордмед-Издат», 1997. – 160 с.

2.   Романенко И.В. Социальное и экономическое прогнозирование: Конспект лекций. – СПб.: Издательство Михайлова В.А., 2000 г. – 64 с.

3.   Прогнозирование и финансирование экономики в условиях рыночных отношений. – М.: Мысль, 1970. – 448 с.

4.   Рябушкин Б.Т. Применение статистических методов в экономическом анализе и прогнозировании. – М.: Финансы и статистика, 1987. – 75 c.

5.   Статистическое моделирование и прогнозирование: под ред. А.Г. Гранберга. – М.: Финансы и статистика, 1990. – 382 с.

6.   Грисеев Ю.П. Долгосрочное прогнозирование экономических процессов: – Киев: Наукова думка, 1987 – 131 с.

7.   Шибалкин О.Ю. Проблемы и методы построения сценариев социально-экономического развития. – М.: Наука, 1992 – 176 с.

8.   Суворов А.В. Методы построения макроэкономических сценариев социально-экономического развития// Проблемы прогнозирования. – 1993. – №4 – сс. 27-39

9.   Калинина А.В. Современный экономический анализ и прогнозирование (микро- и макроуровень): Учебное пособие // А.В. Калинина и др., Межрегиональная Академия управления персоналом, 2-е изд. –Л.: МАУП, 1998.

10.              Глущенко В.В. Прогнозирование –2-е изд., Испр. и доп. –СПб: СПГУВК, 1999. –245 с.

Приложение А:

Таблица 1

Этапы	Стадии
Общая постановка задачи	1.   Общее знакомство с проблемой, указание цели; 2.   Определение используемых понятий; 3.   Сбор и анализ данных, оценка их точности; 4.   Анализ различных возможных общих постановок задач с точки зрения существования и единственности их решения и его использования; уточнение цели.
Построение конструкций для решения задачи	1.   Формулировка априорных предположений и построение знаковой модели для математической постановки задачи; 2.   Математическая постановка задачи.
Решение задачи	1.   Построение алгоритма решения математической задачи; 2.   Получение решения математической задачи (обработка данных).
Интерпретация решений	1.   Проверка полученного решения в соответствии с известными принципами и законами и экспериментальными данными; 2.   Определение области применимости и точности полученного решения. Перспектива использования в практических и теоретических целях.

Приложение В:

Таблица 2 Принципы системного подхода

Наименование принципа	Его содержание
Целостности	Проблема анализа рыночного спроса рассматривается как самостоятельная проблема или как часть другой, более общей, проблемы, в которую она входит. Система. Выделенная для самостоятельного исследования, должна иметь возможность изменять своё состояние (движение) в зависимости от состояния старших или младших (в иерархическом смысле) систем.
Многомерности	Проблема анализа рыночного спроса рассматривается с позиции таких концепций, которые учитывают основные существенные факторы и взаимовлияние на спрос сопутствующих и конкурирующих видов товаров.
Неопределённости и стохастичности	Изменение рыночного спроса происходит под влиянием различных воздействий. Анализ показателей спроса должен производиться своевременно (в реальном масштабе времени), а математические зависимости, описывающие закономерности рыночного спроса, должны содержать в своей структуре модель прогнозирования. Кроме того, необходимо учитывать, что исходная информация, которую реально удастся собрать и подготовить для решения проблемы, оказывается, как правило, в значительной степени неполной и неточной. Статистическому анализу может быть подвергнута лишь некоторая часть всей совокупности микроэкономических параметров (характеристик), статистическое обследование всей генеральной совокупности затрудняется малым объёмом наблюдений.

Приложение С:

Таблица 3

Направления и методы прогнозных исследований в микроэкономике.

№ п/п	Методы прогнозирования	Краткосрочное	Среднесрочное	Долгосрочное
1	Корреляционно-регресионный анализ временных тенденций **	++	++	-
2	Метод экспоненциального сглаживания **	+	++	-
3	Экстраполяция временных тенденций по отшибающим кривым **	-	-	+
4	Метод статистического моделирования временных тенденций **	++	++	-
5	Анкетные опросы экспертов	+	++	-
6	Выработка коллективного мнения экспертов	-	++	+
7	Системный анализ результатов фундаментальных исследований *	-	+	++
8	Структурные схемы целей развития экономической системы и ее отдельных подсистем	-	-	+
9	Сценарий действий экономических структур	-	+	++
10	Игровое моделирование **	-	++	+
11	Генерация идей в ходе «мозговой атаки»	-	++	+
12	Морфологический анализ *	-	+	++
13	Историческая аналогия *	-	-	+

«-» - применение метода прогнозирования невозможно или нецелесообразно;

«+» - применение метода прогнозирования целесообразно и обосновано;

«++» - метод находит преимущественное применение при прогнозировании;

* - метод прогнозирования требует периодического учета фактора старения информации;

** - устаревшая исходная информация может оказать существенное влияние на конечный результат (учет фактора старения информации требует постоянного учета в реальном масштабе времени).