Навигация
Определить параметры h ФПВ
1. Определить параметры h ФПВ
2. Построить ФПВ случайного процесса
3. Определить первый и второй (m1 и m2) начальные моменты, а также дисперсию Д(х) случайного процесса.
| 15(65) | 17 | 4 | 35 | 0.3 | |
| 16(66) | 18 | 3 | 35 | 0.3 | |
| 17(67) | 19 | 2 | 40 | 0.2 | |
| 18(68) | 20 | 3 | 40 | 0.2 | |
| 19(69) | 21 | 4 | 45 | 0.2 | |
| 20(70) | 22 | 5 | 45 | 0.2 | |
| 21(71) | 23 | 6 | 50 | 0.18 | |
| 22(72) | 24 | 5 | 50 | 0.18 | |
| 23(73) | 25 | 4 | 55 | 0.16 | |
| 24(74) | 26 | 3 | 55 | 0.16 | |
| 25(75) | 27 | 2 | 60 | 0.15 | |
| 26(76) | 28 | 3 | 60 | 0.15 | |
| 27(77) | 29 | 4 | 65 | 0.14 | |
| 28(78) | 30 | 5 | 65 | 0.12 | |
| 29(79) | 29 | 6 | 60 | 0.12 | |
| 30(80) | 28 | 5 | 60 | 0.13 | |
| 31(81) | 27 | 4 | 60 | 0.13 | |
| 32(82) | 26 | 3 | 55 | 0.15 | |
| 33(83) | 25 | 2 | 55 | 0.15 | |
| 34(84) | 24 | 3 | 50 | 0.16 | |
| 35(85) | 23 | 4 | 50 | 0.16 | |
| 36(86) | 22 | 3 | 40 | 0.16 | |
| 37(87) | 21 | 2 | 40 | 0.18 | |
| 38(88) | 20 | 3 | 35 | 0.18 | |
| 39(89) | 19 | 4 | 35 | 0.2 | |
| 40(90) | 18 | 5 | 30 | 0.2 | |
| 41(91) | 17 | 6 | 30 | 0.25 | |
| 42(92) | 16 | 5 | 28 | 0.25 | |
| 43(93) | 15 | 4 | 28 | 0.3 | |
| 44(94) | 14 | 3 | 26 | 0.3 | |
| 45(95) | 13 | 2 | 26 | 0.4 | |
| 46(96) | 12 | 3 | 25 | 0.4 | |
| 47(97) | 11 | 4 | 25 | 0.5 | |
| 48(98) | 10 | 5 | 22 | 0.5 | |
| 49(99) | 9 | 6 | 22 | 0.6 | |
| 50(100) | 8 | 4 | 22 | 0.6 |
Для защиты курсовой работы студент должен знать следующие вопросы:
1. Для чего прибегают к дискретизации непрерывных сигналов?
2. Что дает уплотнение каналов?
3. Почему дискретные системы помехоустойчивее непрерывных?
4. Этапы дискретизации.
5. Шаг дискретизации.
6. Теорема В.А. Котельникова
7. Что влияет на величину шага дискретизации по времени?
8. Из чего исходят, выбирая величину шага квановая по уровню?
9. Причины погрешности, возникающих при восстановлении непрерывного сигнала по его отсчетам.
10. Причина погрешностей при дискретизации сигналов.
11. В каких случаях возможно определение полной погрешности?
12. Из чего складывается полная погрешность дискретизации?
13. Когда полная погрешность будет равна нулю?
14. Определение полной погрешности при дискретизации детерминированного сигнала.
15. Определение полной погрешности при дискретизации случайного сигнала.
V. КОНТРОЛЬНЫЕ ЗАДАНИЯ
В контрольной работе внимание уделяется вопросам количественной оценке сигналов, спектральному анализу, амплитудно-частотным и фазо-частотным характеристикам, модуляции и детектированию, а также помехоустойчивому кодированию.
Каждый студент выполняет 4 из девяти работ в соответствии с индивидуальным заданием или 4 задачи из таблицы 4.1. Студент выбирает номера задач по последней цифре шифра (номера зачетной книжки).
Таблица 4.1.
| Последняя цифра шифра Номер задач | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1-задача | 9 | 2 | 9 | 1 | 9 | 2 | 1 | 9 | 2 | 1 |
| 2-задача | 7 | 4 | 7 | 3 | 8 | 4 | 4 | 8 | 3 | 3 |
| 3-задача | 5 | 6 | 6 | 6 | 5 | 5 | 6 | 5 | 6 | 5 |
| 4-задача | 3 | 8 | 4 | 8 | 3 | 7 | 7 | 3 | 8 | 7 |
Задача 1
Задан источник сообщений А=![]() с вероятностями, представленными в табл. 2 в зависимости от последней цифры шифра.
с вероятностями, представленными в табл. 2 в зависимости от последней цифры шифра.
Таблица 4.2.
| Последняя цифра шифра Номер задач | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Р (а1) | 0,2 | 0,3 | 0,15 | 0,25 | 0,15 | 0,2 | 0,25 | 0,4 | 0,2 | 0,1 |
| Р (а2) | 0,3 | 0,2 | 0,35 | 0,2 | 0,2 | 0,35 | 0,2 | 0,2 | 0,3 | 0,2 |
| Р (а3) | 0,25 | 0,15 | 0,3 | 0,1 | 0,3 | 0,25 | 0,3 | 0,3 | 0,4 | 0,3 |
| Р (а4) | 0,15 | 0,1 | 0,1 | 0,15 | 0,1 | 0,5 | 0,1 | 0,2 | 0,3 | 0,4 |
| Р (а5) | 0,1 | 0,25 | 0,2 | 0,1 | 0,2 | 0,1 | 0,15 | 0,1 | 0,2 | 0,3 |
1. Найти количество информации, содержащейся в каждом из символов источника при их независимом выборе.
Вычислить энтропию и избыточность заданного источника.
2. Показать, что при равных объемах алфавитов N, энтропия H(A) имеет максимальное значение Hmax (A)= log2 N при равновероятных символах.
3. Описать физические характеристики дискретных каналов и сигналов, а также процесс преобразования дискретных сообщений в электрические сигналы.
Задача 2
Задан канал связи с полосой частот Fк, время использование Tк. В канале действует шум с равномерной спектральной плотностью мощности Gш, физический объем канала Vк
Таблица 4.3.
| Параметры | Последняя цифра шифра | |||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| Fк, кГц | 10 | 10 | 20 | 10 | 1 | 10 | 5 | 7 | 10 | 5 |
| Тк, с | 10 | 5 | 10 | 1 | 10 | 5 | 2 | 7 | 10 | 1 |
| Gш, МВТ/Гц | 10-4 | 10-4 | 10-3 | 10-4 | 10-3 | 10-3 | 10-5 | 10-4 | 10-5 | 10-3 |
| Vк | 106 | 106 | 107 | 105 | 106 | 106 | 105 | 106 | 104 | 105 |
1. Найти предельную мощность сигнала, который может быть передан по данному каналу.
2. Представить структурную схему системы передачи информации
3. Привести классификацию и дать описание помех возникающих в канале связи.
Задача 3
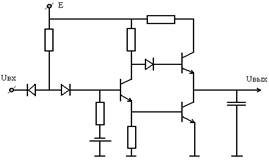
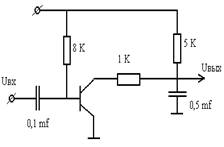
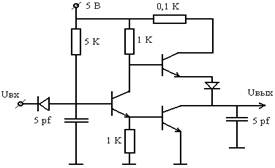
Задан стационарный случайный процесс x(t) который имеет одномерную функцию плотности вероятности (ФПВ) мгновенных значений W(x). График и параметры сигнала приведены в табл. 4.4.
[11]
[12]
[13]
[14]
[15]
[16]
Похожие работы
... . 1.2. Если в данный момент времени , это означает, что направление тока в проводнике совпадает с направлением, указанным стрелкой, т. е. положительные заряды перемещаются в направлении стрелки. В теории электрических цепей допускается возможность однозначной, не зависящей от выбора пути, оценки электрических напряжений меду любыми двумя зажимами исследуемой электрической цепи. Это позволяет ...
... к расчету. ¨ В оглавлении указываются названия разделов и номера страниц, соответствующие началам разделов. ¨ Во введении кратко рассматривается общенаучное значение теории электрических цепей (ТЭЦ) для изучения электромагнитных явлений и их практического приложения. Описываются связи ТЭЦ с соответствующими разделами математики и физики, а также с различными ...
... любой из ветвей выбранного сечения приводит к связному графу. Отмеченные выше понятия и положения будут использованы в дальнейшем при расчете электрических цепей по методам, вытекающим из законов Кирхгофа. Теорема замещения В теории электрических цепей как при доказательствах ряда ее положений, так и при численных расчетах используется теорема замещения: значения всех напряжений и токов в ...
... Мгновенное напряжение на проводимости G =10 Cм при заданном токе i=12sin(ωt+φ) равно: u=1,2sin(ωt + φ) 4. Электрические цепи при гармоническом воздействии в установившемся режиме Основные свойства линейных цепей: Принципа суперпозиции. Независимыми называют узлы, которые: отличаются одной ветвью. Независимыми называются контура, которые: отличаются одной ...







0 комментариев