Вывод уравнения колебания в электрических проводах.
Электрический ток в проводах характеризуется величиной
и напряжением 
которые зависят от координат Х точки провода и от времени t. Рассмотрим элемент провода ∆Х. Можем написать, что падение напряжения на элементе ∆Х равно -
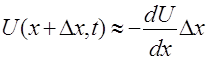.Это падение напряжения складывается из омического, равного 
и индуктивного, равного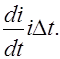 
Итак
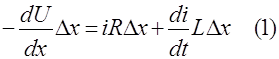
где R и L –сопротивление и коэффициент индуктивности рассчитанные на единицу длинны провода. Знак минус взят потому, что ток течёт в направлении, обратном возрастанию U.Сокращая на ∆Х, получим уравнение
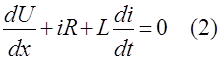
Далее разность токов, выходящего из элемента ∆Х за время ∆t , будет
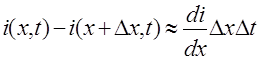
Она расходуется на зарядку элемента, равную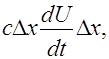 
и на утечку через боковую поверхность провода в следствии несовершенства изоляции, равную 
Здесь А- коэффициент утечки. Приравняем эти выражения
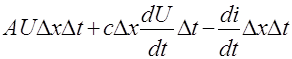
Сократим на 
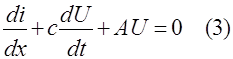
Уравнения (2) и (3) принято называть телеграфными уравнениями. Составим систему уравнений
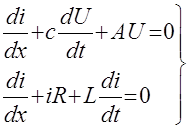
Из этой системы уравнений можно получить уравнение, содержащее только искомую функцию, и уравнение, содержащее только искомую функцию .
Продифференцируем члены уравнения (3) по Х; члены уравнения (2) продифференцируем по t и умножим их на С.
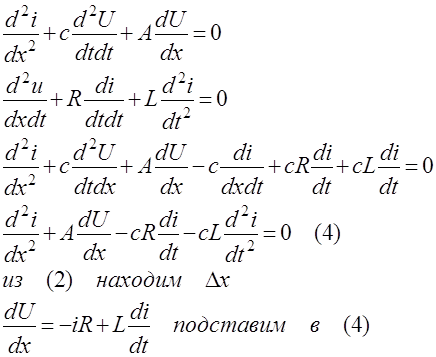
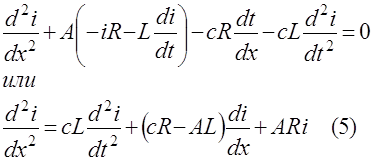
Аналогичным образом получим уравнение для определения
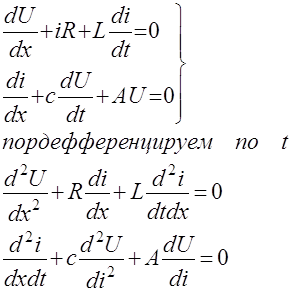
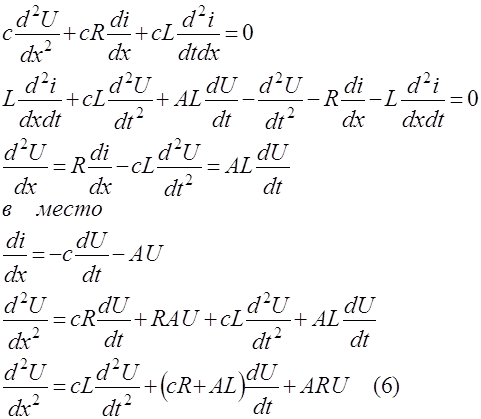
Если можно пренебречь утечкой через изоляцию (А=0) и сопротивлением (R=0), то уравнения (5) и (6) переходят в волновые уравнения:
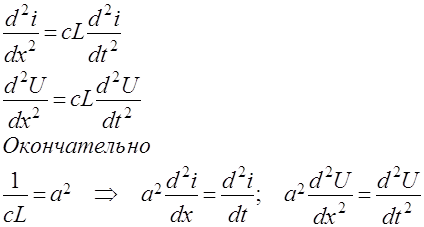
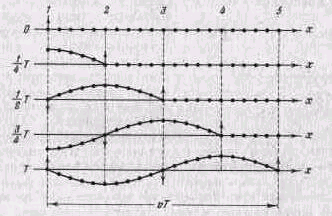
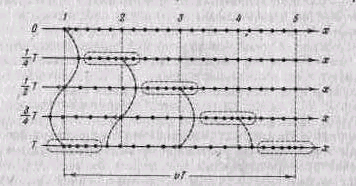
Исходя из физических условий формулируются граничные и начальные условия задачи.
Навоийский Государственный горный институтГорный факультет
Кафедра «Высшей математики»
Волновые уравнения
Подготовил: студент 2-го курса группы 20-02 ГД
Дерюга А.М.
Навоий 2004 г.
Похожие работы
... с u его важнейшей акустической характеристикой. Название величины связано с формальной аналогией между уравнениями (2.14) и законом Ома (р аналогично разности потенциалов, v - силе тока). § 2. Упругие волны в газах и жидкостях 1. Волновое уравнение. Мы рассматриваем здесь газ или жидкость (так же как твердое тело в предыдущих параграфах) как сплошную непрерывную среду, отвлекаясь от его ...
... где. Функция f не должна быть решением волнового уравнения. Мы видим, что второе решение существует и отлично от нуля при t>0. Таким образом, теорема о нарушении единственности решения задачи Коши для волнового уравнения доказана. Применение результатов Полученное доказательство служит обоснованию метода получения новых решений, описанного в [2], [3] и др. статьях авторов. Оно имеет прямую ...
... при наличии сил, действующих на частицу, вместо Е в уравнение (16) нужно ввести кинетическую энергию частицы Т = Е –U. Произведя такую замену, мы придем к уравнению (12). Приведенные нами рассуждения не могут рассматриваться как вывод уравнения Шрёдингера. Их цель — пояснить, каким образом можно было прийти к установлению вида волнового уравнения для микрочастицы. Доказательством же правильности ...
... энергии одного электрона на их максимальное число, соответствующее определенному энергетическому уровню. Таким образом, мы выходим на представление о существовании в каждом атоме одной или нескольких изоэнергетических поверхностей, которые следует отнести к наиболее сохраняющимся физическим величинам. По всей видимости, эта новая не совсем привычная величина определяет те внешние пространственные ...
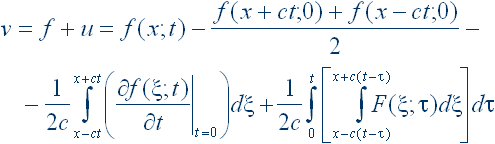
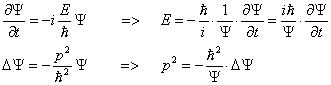
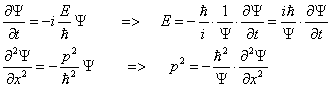
0 комментариев