Лабораторная работа № 2
Интерполирование и экстраполирование данных.
Интерполяционный многочлен Лагранжа.
Многочлен Лагранжа, принимающий заданные значения в узловых точках имеет вид:
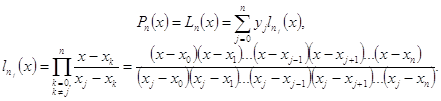
Задание . Восстановить многочлен Лагранжа, удовлетворяющий приведенным исходным данным.
 |
Пример:
Варианты:
| 1). | 0 | 1 | 2 | 5 |
| |||||
| | 2 | 3 | 12 | 147 |
| |||||
| 2). | -2 | 1 | 2 | 4 |
| |||||
| | 25 | -8 | -15 | -23 |
| |||||
| 3). | -2 | -1 | 0 | 1 | 2 | ||||||
| | 6 | 0 | 2 | 0 | 6 | ||||||
| 4). | 0 | 1 | 2 | 5 |
| |||||
| | 3 | 4 | 13 | 148 |
| |||||
| 5). | -2 | 1 | 2 | 4 |
| |||||
| | 26 | -7 | -14 | -22 |
| |||||
| 6). | -2 | -1 | 0 | 1 | 2 | ||||||
| | 5 | 0 | 1 | 0 | 5 | ||||||
| 7). | -1 | 0 | 1 | 4 |
| |||||
| | 2 | 3 | 12 | 147 |
| |||||
| 8). | 1 | 2 | 3 | 6 |
| |||||
| | 2 | 3 | 12 | 147 |
| |||||
| 9). | -3 | 0 | 1 | 3 |
| |||||
| | 25 | -8 | -15 | -23 |
| |||||
| 10). | -1 | 2 | 3 | 5 |
| |||||
| | 25 | -8 | -15 | -23 |
| |||||
| 11). | -3 | -2 | -1 | 0 | 4 | ||||||
| | 6 | 0 | 2 | 0 | 6 | ||||||
| 12). | -1 | 0 | 1 | 2 | 3 | ||||||
| | 6 | 0 | 2 | 0 | 6 | ||||||
| 13). | 2 | 3 | 4 | 7 |
| |||||
| | 2 | 3 | 12 | 147 |
| |||||
| 14). | -2 | -1 | 0 | 3 |
| |||||
| | 2 | 3 | 12 | 147 |
| |||||
| 15). | -4 | -1 | 0 | 2 |
| |||||
| | 25 | -8 | -15 | -23 |
| |||||
| 16). | 0 | 3 | 4 | 6 |
| |||||
| | 25 | -8 | -15 | -23 |
| |||||
| 17). | -1 | 0 | 1 | 4 |
| |||||
| | 3 | 4 | 13 | 148 |
| |||||
| 18). | 1 | 2 | 4 | 6 |
| |||||
| | 1 | 2 | 34 | 146 |
| |||||
| 19). | -3 | 0 | 1 | 3 |
| |||||
| | 26 | -7 | -14 | -22 |
| |||||
| 20). | -1 | 2 | 3 | 5 |
| |||||
| | 26 | -7 | -14 | -22 |
| |||||
| 21). | -3 | -2 | -1 | 0 | 1 | ||||||
| | 7 | 1 | 3 | 1 | 7 | ||||||
| 22). | -1 | 0 | 1 | 2 | 3 | ||||||
| | 5 | -1 | 1 | -1 | 5 | ||||||
| 23). | -1 | 0 | 1 | 2 | 3 | ||||||
| | 2 | 1 | 0 | 1 | 10 | ||||||
| 24). | -2 | -1 | 0 | 1 |
| |||||
| | 1 | 6 | 5 | 4 |
| |||||
| 25). | -3 | -2 | -1 | 0 |
| |||||
| | 40 | 27 | 12 | 1 |
| |||||
| 26). | -2 | -1 | 0 | 1 | 2 | ||||||
| | -27 | -4 | -1 | -6 | -7 | ||||||
| 27). | -1 | 0 | 1 | 2 |
| |||||
| | -5 | -10 | -1 | 34 |
| |||||
| 28). | -2 | -1 | 0 | 1 | 2 | ||||||
| | 16 | -1 | 0 | 1 | 8 | ||||||
| 29). | -2 | -1 | 0 | 1 | 2 | ||||||
| | -23 | -6 | 1 | -2 | 9 | ||||||
| 30). | 1 | 2 | 3 | 4 |
| |||||
| | 1 | 2 | 13 | 40 |
| |||||
Похожие работы
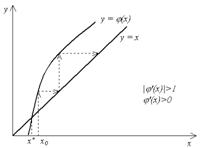
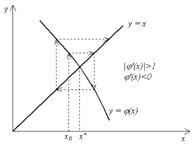
... при построении итерационных методов решения уравнения =0. Например взяв за корень линейного интерполяционного алгебраического многочлена, построенного по значениям и в узле или по значениям и в узлах и , приходят соответственно к методу Ньютона и метода секущих , где - разделенная разность функций для узлов и . Другой подход к построению численных методов решения уравнения ...
... (5.16) Непосредственное использование оценок погрешности (5.4), (5.8) и (5.12) неудобно, так как при этом требуется вычисление производных функции f(x). В вычислительной практике используются другие оценки. Вычтем из равенства (5.15) равенство (5.16): Ih/2 – Ih » Chk(2k – 1). (5.17) Учитывая приближенное равенство (5.16), получим следующее приближенное ...
... суммы и позволит вычислить приближенное значение приращения Dy: где Метод четвертого порядка для q = 3, имеет вид где Особо широко известно другое вычислительное правило Рунге-Кутта четвертого порядка точности: где Метод Рунге-Кутта имеет погрешность четвертого порядка (~ h4 ). Правило Рунге. Если приближенный метод имеет порядок погрешности m, то погрешность можно приближенно ...
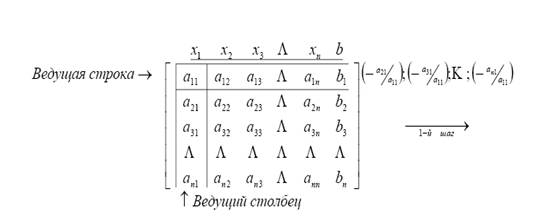
... на языке Turbo Pascal 7.0 для решении систем линейных алгебраических уравнений, используя метод простой итерации. 1.2 Математическая формулировка задачи Пусть А – невырожденная матрица и нужно решить систему где диагональные элементы матрицы А ненулевые. 1.3 Обзор существующих численных методов решения задачи Метод Гаусса В методе Гаусса матрица СЛАУ с помощью равносильных ...
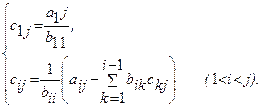
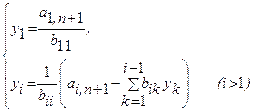
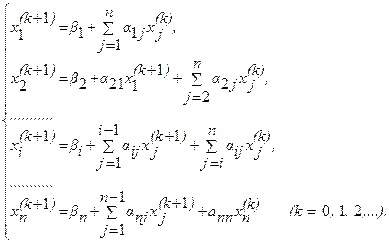
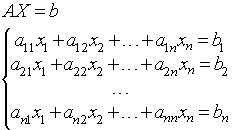
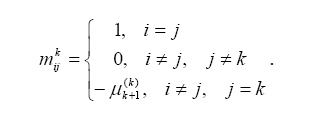
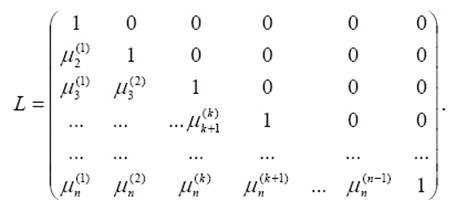
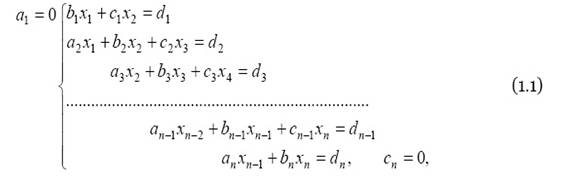
0 комментариев