 КУРСОВОЙ
ПРОЕКТ
КУРСОВОЙ
ПРОЕКТ
по дисциплине «Информатика»
студента группы КС-31
Кузнецова Дмитрия Олеговича
![]()
![]()
СОДЕРЖАНИЕ
ВВЕДЕНИЕ 2
1.Задача 1
Постановка задачи
Решение 4
2. Задача 2
2.1.Постановка задачи
2.2.Решение 6
3.Задача 3
3.1.Постановка задачи
3.2.Решение 10
4.Задача 4
4.1.Постановка задачи
4.2.Решение 15
СПИСОК ЛИТЕРАТУРЫ 16
ВВЕДЕНИЕ
Основой автоматизации умственного труда человека является широкое внедрение вычислительной техники во все сферы деятельности человека . Применение ЭВМ ускорило процесс математизации науки и техники . Расширяется круг профессий ,для которых математическая грамотность и наличие практических навыков применения ЭВМ становятся необходимыми.
Решение технической или научной задачи включает её математическое описание на языке уравнений, функций .Очень часто математическая формулировка задачи может оказаться непереводимой на язык ЭВМ ,так как ЭВМ выполняет только арифметические действия.
Численный метод решения задачи –это определённая последовательность операций над числами , язык которого числа и арифметические действия .Численные методы легко реализуются на ЭВМ ,что делает эти методы мощным и универсальным инструментом. Процесс решения инженерной задачи на ЭВМ сложный и длительный .Он включает в себя этапы, требующие от разработчика профессиональной подготовки и грамотности. Для снижения трудоёмкости , на всех типах ЭВМ создан мощный аппарат технологической поддержки работы пользователя ЭВМ.
1.Задача 1
1.1.Постановка задачи
Необходимо графически определить один корень уравнения . Уточнить корень уравнения с точностью Е=0,001 методом Ньютона. Дано нелинейное уравнение :
tg(x+)=x2
где =0,5 и =0,2
1.2.Решение
Для того ,чтобы определить корень ,преобразуем уравнение к виду :
tg(0.5x+0.2)=x2
Построим графики двух функций :
y1= tg(0.5x+0.2) и y2=x2;
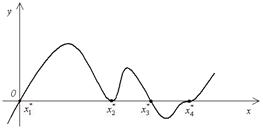
Кривые на рис.1 описаны следующим образом:
y1= tg(0.5x+0.2) функция периодическая ,её значения сведём в таблицу 1.1
Таблица 1.1.
| x | -3.1 | -3 | -2 | -1 | 0 | 1 | 2 | 2.1 | 2.2 |
| y | -4.45 | -2.57 | -1.02 | -0,3 | 0,2 | 0,84 | 2.57 | 3.0 | 3.6 |
y2=x2 – парабола
y2=0 когда x=0
y2=4 при x=2
По графику определяем ,что уравнение имеет несколько корней .Для уточнения корня выберем интервал 0,1 .Уточняем корень по формуле Ньютона:
xn+1=
xn- 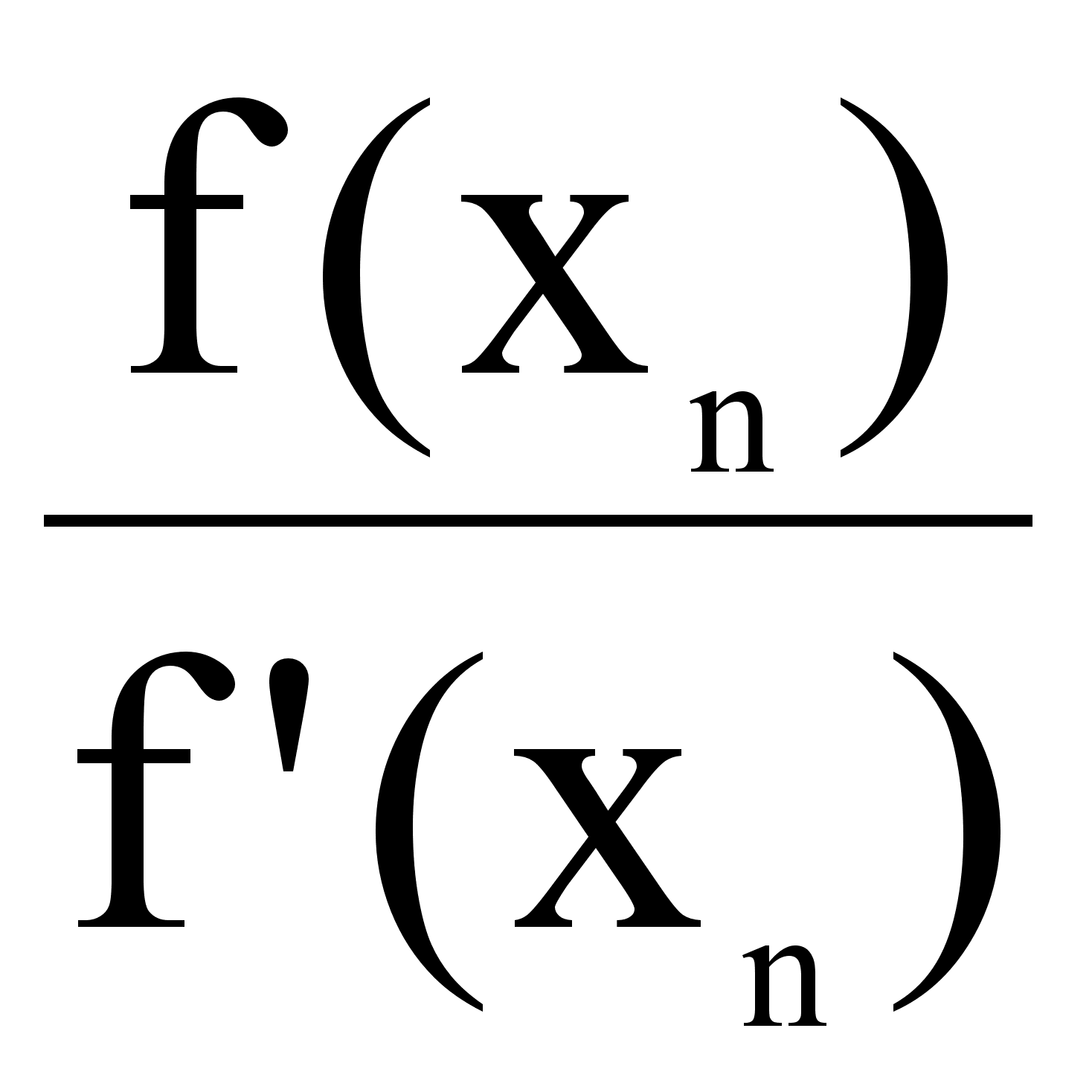
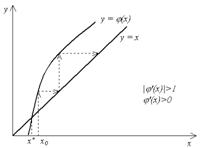
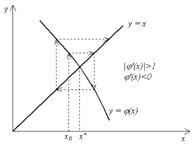
Необходимо выбрать начальное значение x0 , исходя из условия сходимости:
f(x0)f "(x0)>0
f(x)= tg(0.5x+0.2) – x2
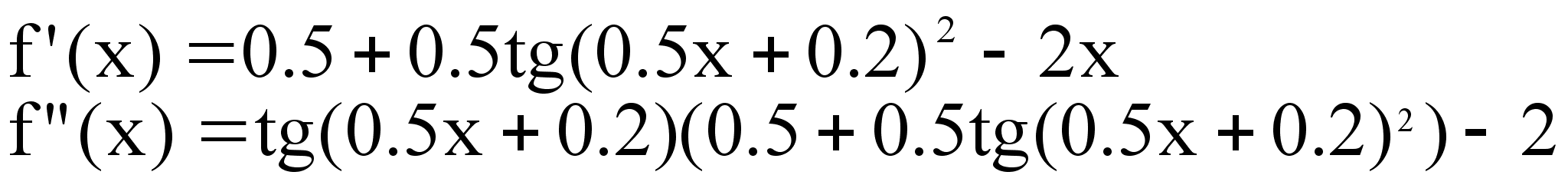
Проверяем условия сходимости для x=0 :
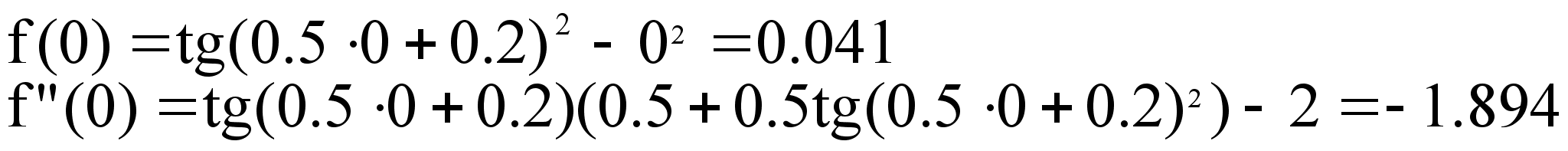
f(0)f"(0)0,условие соблюдается
берём за x0=1
и условие:
Т=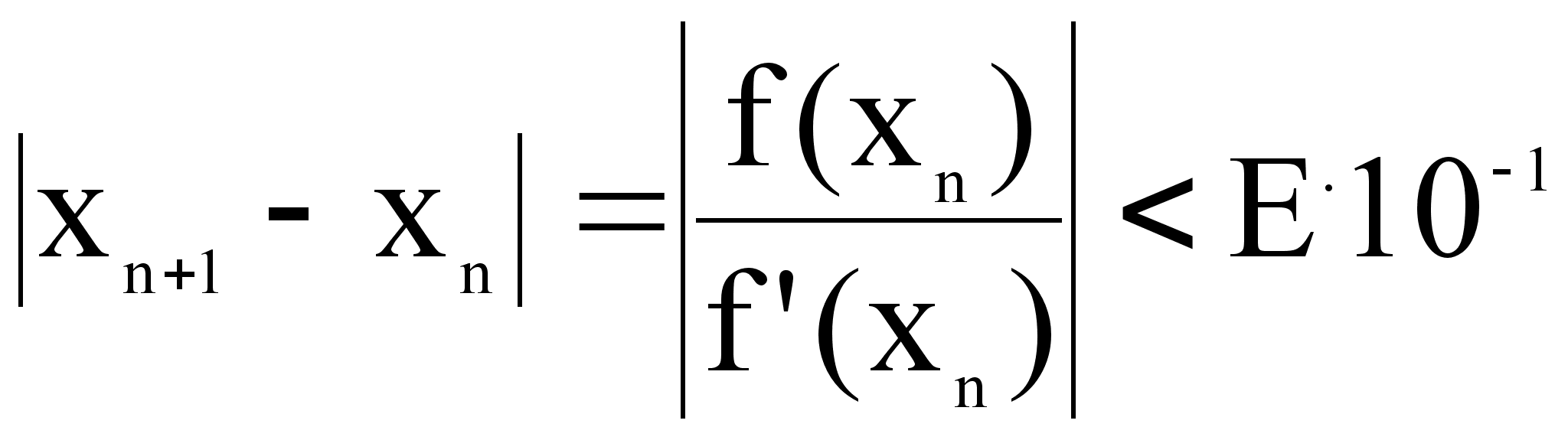
Решение запишем в виде таблицы:
| n | x n | f(x n) | f '(x n) |
| T |
Похожие работы
помощью метода Рунге-Кутты четвертого порядка с автоматическим выбором шага на отрезке . Задачу можно решить аналитически, найдя решение дифференциального уравнения и подставив в него начальное условие, тем самым, отыскав требуемую интегральную кривую. Но для нас интерес представляет решение данной задачи с применением численного метода, а конкретнее – метода Рунге-Кутты 4-го порядка с ...
... (5.16) Непосредственное использование оценок погрешности (5.4), (5.8) и (5.12) неудобно, так как при этом требуется вычисление производных функции f(x). В вычислительной практике используются другие оценки. Вычтем из равенства (5.15) равенство (5.16): Ih/2 – Ih » Chk(2k – 1). (5.17) Учитывая приближенное равенство (5.16), получим следующее приближенное ...
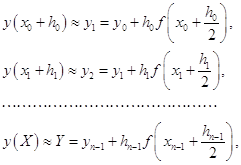
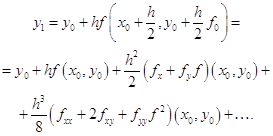
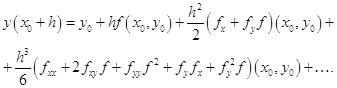
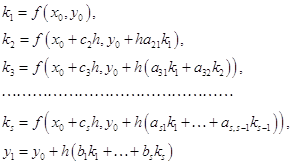
0 комментариев