Лекции (1-18) по мат. анализу 1 семестр

По всем вопросам и по дальнейшему пополнению лекций обращаться на ящик

van_mo_mail@mtu-net.ru или на сотовый:

8-901-7271056 спросить Ваню

Ведущая: Голубева Зоя Николаевна

Дата: вторник, 5 сентября 2000 г.

Тема: Введение

Условные обозначения:

: - так, что def – по определению

 – включает ’’’ – [dⁿf(x)]/dxⁿ=(d/dx)([d^n-1f(x)]/dxⁿ)

 - следует, выполняется

 - тогда и только тогда

 - любой

 - существует

] – пусть

! – единственный

[x] – целая часть

~ - эквивалентно

о - малое

Все R представляют десятичной дробью.

Все Q представляют конечной дробью, либо периодичной дробью.

Все иррациональные числа представляют бесконечной десятичной дробью ( не периодичной).

Рассмотрим числовую ось. Числовая ось – направленная прямая с отмеченной точкой и отмеченным масштабом.

x

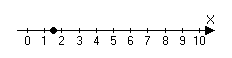
0 – отвечает за ноль.

Отрезок [0;1] отвечает за единицу

Единица за единицу.

Каждой точки х на числовой прямой отвечает некоторое действительное число. Если длинны отрезков [0;x] из заданного масштаба соизмеримы, тогда числу х отвечает рациональное число. Если не соизмеримы, то иррациональны.

Каждому R отвечает точка на числовой прямой и наоборот, каждой точке отвечает R.

Основные числовые множества.

x

Отрезок: [/////////] x

a b

Обозначается [a;b] ab

Частный случай отрезка точка

Или axb – в виде неравенства.

х

Интервал: (/////////) x – множество точек на числовой прямой.

a b

Обозначается (a;b) или в виде неравенства aε

n>log₂ε

N=[log₂ε]+1

Правило формирования обратного утверждения: нужно поменять местами значки  и , а знак неравенства на дополнительный.

Пример:

Утверждение lim a_n=a0 NN:n>N  a_n-a0 NN: n>N  a_n-aN  a_n-a0 возьмем ε=1  N:n>N  a_n-aN

Теорема (о единстве предела сходящейся последовательности).

Если lim a_n=a 0 для определенности пусть b>a N₁:n>N₁ a_n-aN₂  a_n-b1/ε N=max{N₁;N₀}

Тогда n>N  1/a_nN₀ зададим ε>0 положим ε=1/ε>0

N₁:n>N₁ _nN  1/_n=, то есть 1/_n – бесконечно большая.

Основные теоремы о существование предела последовательности.

Теорема Вейрштрасса:

Пусть a_n- ограниченная и моннатонна. Тогда  lim a_n=а