ГАУСС (Gaus ) Карл Фридрих (1777-1855), нем. математик, ин. ч.-к. (1802) и ин. поч. ч. (1824) Петерб. АН. Для творчества Г. характерна органич. связь между теоретич. и прикладной матедатикой, широта проблематики. Тр. Г. оказали большое влияние на развитие алгебры (доказательство осн. теоремы алгебры), теории чисел (квадратичные вычеты), дифференц. геометрии (внутр. геометрия поверхностей), матем. физики (принцип Г.), теории электричества и магнетизма, геодезии (разработка метода наименьших квадратов) и мн. разделов астрономии.
2. КРАТКАЯ ТЕОРИЯ .Пусть дана система линейных уравнений
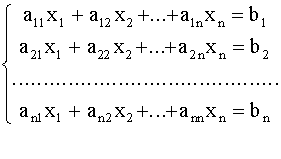 (1)
(1)
Коэффициенты a11,12,..., a1n, ... , an1 , b2 , ... , bn считаются заданными .
Вектор -строка н x1 , x2 , ... , xn э - называется решением системы (1), если при подстановке этих чисел вместо переменных все уравнения системы (1) обращаются в верное равенство.
Определитель n-го порядка D = з A к = з a ij з , составленный из коэффициентов при неизвестных , называется определителем системы (1). В зависимости от определителя системы (1) различают следующие случаи.
a). Если D № 0 , то система (1) имеет единственное решение, которое может быть найдено методом ГАУССА .
б). Если D = 0 , то система (1) либо имеет бесконечное множество решений , либо несовместна ,т.е. решений нет.
2. МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ1. Рассмотрим систему 3-х линейных уравнений с тремя неизвестными.
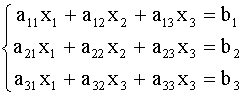 (2).
(2).
Метод Гаусса решения системы (2) состоит в следующем:
Разделим все члены первого уравнения на ![]() , а затем ,умножив полученное уравнение на
, а затем ,умножив полученное уравнение на ![]() , вычтем его соответственно из второго и третьего уравнений системы (2). Тогда из второго и третьего уравнений неизвестное
, вычтем его соответственно из второго и третьего уравнений системы (2). Тогда из второго и третьего уравнений неизвестное ![]() будет исключено ,и получиться система вида:
будет исключено ,и получиться система вида:
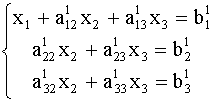 (3)
(3)
Теперь разделим второе уравнение системы (3) на![]() , умножим полученное уравнение на
, умножим полученное уравнение на ![]() и вычтем из третьего уравнения. Тогда из третьего уравнения неизвестное
и вычтем из третьего уравнения. Тогда из третьего уравнения неизвестное ![]() будет исключено и получиться система треугольного вида :
будет исключено и получиться система треугольного вида :
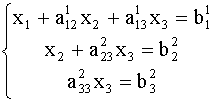 (4)
(4)
Из последнего уравнения системы (4) находим ![]() ,подставляя найденное
,подставляя найденное
подставляя найденное значение в первое уравнение , находим ![]() .
.
Методом Гаусса решить систему:
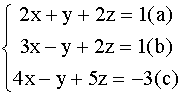
Решение: Разделив уравнение (а) на 2 , получим систему 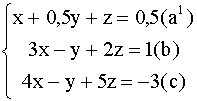
Вычтем из уравнения (b) уравнение ![]() , умноженное на 3, а из уравнения (c) -
, умноженное на 3, а из уравнения (c) -
уравнение ![]() , умноженное на 4.
, умноженное на 4.
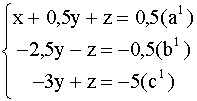
Разделив уравнение![]() (
(![]() ) на -2,5 , получим :
) на -2,5 , получим : 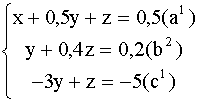
Вычтем из уравнения (![]() ) уравнение
) уравнение ![]() , умноженное на -3:
, умноженное на -3:
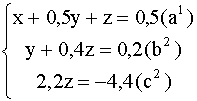
Из уравнения ![]() находим Z=-2; подставив это значение в уравнение
находим Z=-2; подставив это значение в уравнение ![]() , получим Y=0,2-0,4Z=0,2-0,4(-2)=1; наконец , подставив значение Z=-2 и Y=1 в уравнение(a1) , находим X=0,5-0,5Y-Z=0,5-0,5 1 - (-2)=2. Итак, получаем ответ X=2, Y=1, Z=-2 .
, получим Y=0,2-0,4Z=0,2-0,4(-2)=1; наконец , подставив значение Z=-2 и Y=1 в уравнение(a1) , находим X=0,5-0,5Y-Z=0,5-0,5 1 - (-2)=2. Итак, получаем ответ X=2, Y=1, Z=-2 .
Проверка:
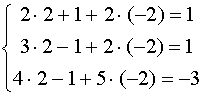
Похожие работы
... 4.Исходный текст программы Составить программу решения систем линейных алгебраических уравнений с квадратной невырожденной матрицей порядка n методом Гаусса с использованием языка С++ . // Решение системы линейных уравнений методом Гаусса. #include<io.h> #include "stdio.h" #include "conio.h" #include <windows.h> #include <iostream> #include <time.h> #include ...
... . Также мы получим графическое отображение процесса интегрирования на участках возрастания и убывания функции. 2. Выбор математической модели задачи Кратко рассмотрим основные методы численного интегрирования и выясним почему метод Гаусса наиболее подходит для решения нашей задачи. 2.1 Метод прямоугольников Метод прямоугольников получается при замене подынтегральной функции на ...
... 1.2 0.4 -0.8 -0.8 3.6 4 4.7 10.4 9.7 9.7 -8.4Результат вычислений по методу Гаусса x1 = 5.0000000000E+00 x2 = -4.0000000000E+00 x3 = 3.0000000000E+00 x4 = -2.0000000000E+00 2.2 Программа решения систем линейных уравнений по методу Зейделя 2.2.1. Постановка задачи. Требуется решить систему линейных алгебраических уравнений с вещественными коэффициентами вида a11x1 + a12x2 + … + a1nxn = ...
... "деление" для матриц не вводится. Для квадратных невырожденных матриц вводится обратная матрица. С понятием обратной матрицы можно познакомиться в рекомендуемой литературе. 2 – ой учебный вопрос РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ МЕТОДОМ ГАУССА Метод Гаусса (или метод последовательного исключения неизвестных) применим для решения систем линейных уравнений, в которых число неизвестных ...
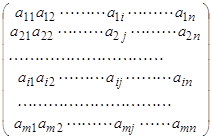
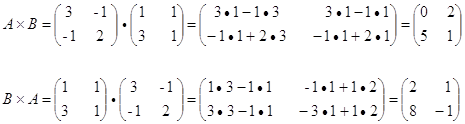
0 комментариев