Середні значення
Статистика оперує такими середніми значеннями: середнє арифметичне, середнє квадратичне, середнє геометричне.
Середнє арифметичне. Нехай ми маємо п об'єктів, у яких виміряно деяку характеристику, що має значення x1, x2, …, xn.
Середнім значенням (або середнім арифметичним) називається таке число ![]() , яке дістають діленням суми всіх даних вибірки x1, x2, …, xn на число цих даних n,
, яке дістають діленням суми всіх даних вибірки x1, x2, …, xn на число цих даних n,
![]()
або ![]() (
(![]() - знак суми – “сигма” велика)
- знак суми – “сигма” велика)
Приклади. 1) Протягом перших п’яти днів березня температура повітря, вимірювана о 8 год. ранку, становила 3°, 5°, 4°, 1°, 2°. Знайти середню температуру за ці дні.
Маємо: ![]()
2) 3 двох учнів треба вибрати одного в баскетбольну команду. Відомі кількості їхніх влучень м'яча в корзину на кожні десять кидків під час тренувань.
Таблиця 1
| Номер тренувань | 1 | 2 | 3 | 4 | 5 |
| Перший учень | |||||
| 4 | 3 | 5 | 3 | 6 | |
| Кількість влучень | Другий учень | ||||
| 5 | 4 | 3 | 6 | 5 | |
Розв'язання.
Знаходимо середню кількість влучень.
Для першого учня:
![]()
Для другого учня:
![]()
Отже, в команду слід узяти другого учня.
Розглянемо деякі властивості середнього арифметичного.
1) Знайдемо відхилення l кожного значення xj від середнього![]() . Різниця х —
. Різниця х —![]() може бути від'ємною або додатною.
може бути від'ємною або додатною.
Сума всіх п відхилень дорівнює нулю. Проілюструємо цю властивість на прикладі. Вихідні дані:. (0; 0; 1; 1; 3;3;3; 5); n= 8; ![]() = 2.
= 2.
2) Якщо до кожного результату спостережень додати деяке число с (константу), то середнє арифметичне ![]() перетвориться в
перетвориться в ![]() + с. Візьмемо, наприклад, попередні 8 значень і додамо до кожного з них по 5. Дістанемо числа 5; 5; 6: 6; 8; 8; 8; 10, середнє арифметичне яких (5 + 5+ 6 + 6 + 8 + 8 + 8+10) : 8 = 7. Середнє на 5 одиниць більше.
+ с. Візьмемо, наприклад, попередні 8 значень і додамо до кожного з них по 5. Дістанемо числа 5; 5; 6: 6; 8; 8; 8; 10, середнє арифметичне яких (5 + 5+ 6 + 6 + 8 + 8 + 8+10) : 8 = 7. Середнє на 5 одиниць більше.
| Значення | Середнє арифметичне | Відхилення |
| 0 | 2 | -2 |
| 0 | 2 | -2 |
| 1 | 2 | -1 |
| 1 | 2 | -1 |
| 3 | 2 | 1 |
| 3 | 2 | 1 |
| 3 | 2 | 1 |
| 5 | 2 | 3 |
| - | ||
| 0 | ||
3) Якщо кожне значення сукупності з середнім ![]() помножити на константу с, то середнє арифметичне стане с
помножити на константу с, то середнє арифметичне стане с![]() . Перевірте властивість, використовуючи попередні дані.
. Перевірте властивість, використовуючи попередні дані.
Якщо величини деяких даних повторюються, то середнє арифметичне визначають за формулою
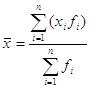 ,де
,де
fi — частота повторення результату xi.
Приклади. 1) Протягом двадцяти днів серпня температура повітря вранці була такою: 17°, 18°, 19°, 20°, 18°, 18°, 18o, 19o, 19°, 20°, 20°, 19°, !9°, 19°, 20°, 19o, 18°, 17°, 16°, 19°.
Знайти середню температуру за цими даними.
Тут окремі значення (17°, 18°, 19°, 20°) повторюються. Середня температура дорівнює:
![]()
2) Подаємо запис обчислення середнього арифметичного при повторенні деяких даних у вигляді таблиці.
Таблиця 3| Вихідні дані | xi | Частота fi | xifi | Остаточне обчислення | ||
| 2 | 6 | 10 | 2 | 2 | 4 |
де I=1,2,3,…,11 |
| 2 | 6 | 10 | 3 | 1 | 3 | |
| 3 | 6 | 11 | 4 | 3 | 12 | |
| 4 | 6 | 12 | 5 | 2 | 10 | |
| 4 | 8 | 12 | 6 | 4 | 24 | |
| 4 | 9 | 15 | 8 | 1 | 8 | |
| 5 | 9 | 15 | 9 | 3 | 27 | |
| 5 | 9 | 15 | 10 | 2 | 20 | |
| 11 | 1 | 11 | ||||
| 12 | 2 | 24 | ||||
| 15 | 3 | 45 | ||||
|
| ||||||
3) За контрольну роботу учні одержали такі оцінки
Оцінки (бали) 5 4 3 2Кількість
учнів 6 7 4 17
Чи достатньо засвоєний матеріал?
Знайдемо середню величину оцінок.
![]()
Ця оцінка є задовільною. Але частота оцінки «2» (мода) дуже висока, вона дорівнює 17. Отже, матеріал засвоєний учнями недостатньо.
Середнє квадратичне відхилення. Ми вже встановили, що сума відхилень даних від середнього значення дорівнює нулю. Тому, якби ми вирішили шукати середній показник відхилень, то він також дорівнював би нулю. В статистиці користуються іншим показником — середнім квадратичним відхиленням, який знаходять так: усі відхилення підносять до квадрата; знаходять середнє арифметичне цих квадратів; із знайденого середнього арифметичного добувають квадратний корінь. Середнє квадратичне відхилення позначають грецькою буквою σ (“сигма” мала):
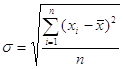
Знаходження середнього квадратичного відхилення подано в таблиці 4.
Таблиця 4| Значення xi | Середнє арифметичне | Відхилення xi — | Квадрат відхилення (xi- | Квадратичне відхилення σ |
| 5 | - 7 | 49 | ||
| 8 | - 4 | 16 | ||
| 10 | - 2 | 4 | ||
| 12 | 0 | 0 | ||
| 17 | 5 | 25 | ||
| 20 | 8 | 64 | ||
|
|
|
|
|
|
У статистиці користуються також величиною σ2 (квадрат середнього квадратичного відхилення), яку називають дисперсією.
Середнє геометричне п додатних чисел х1, х2, х3, ...,хп визначається виразом
![]() , тобто середнє геометричне х1х2х3...п є корінь n-го степеня з добутку всіх xi (і = 1, 2, ...).
, тобто середнє геометричне х1х2х3...п є корінь n-го степеня з добутку всіх xi (і = 1, 2, ...).
У випадку двох чисел а і b середнє геометричне називають середнім пропорційним цих чисел. З рівності тс = аb випливає, що а : mc= тс : b.
На практиці окремим особам, організаціям, керівникам підприємств доводиться розв'язувати різноманітні задачі, пов'язані з використанням поняття моди, медіани, середнього. Наприклад, яких розмірів дитячого взуття слід випускати більше, ніж інших; на якому з міських маршрутів треба пустити автобусів більше, ніж на решті; якого розміру спортивних костюмів слід виготовити найбільше для учнів 10—11 класів тощо.
Розглянуті моду, медіану і середні значення називають мірами центральної тенденції.
Похожие работы
... ВИСНОВОК: на виконання такого завдання студенти в середньому затрачають 11 хв. Середня квадратична для величин х1, х2. .....хn від їх середнього значення х. Середня квадратична незважена буде: (3) Середня квадратична зважена — (4) Середню квадратичну використовують тоді, коли варіанти є відхиленням фактичних величин від їх середньої арифметичної або від заданої норми. СЕРЕДНЯ ...
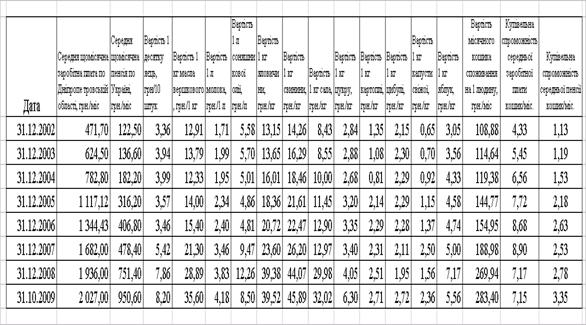
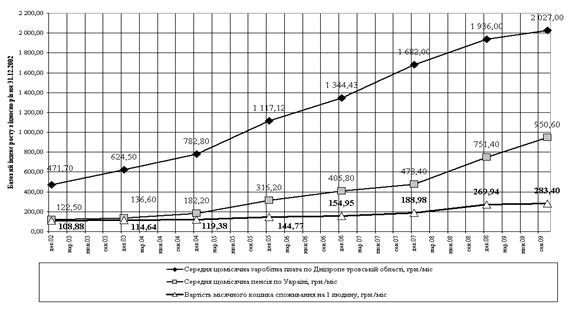
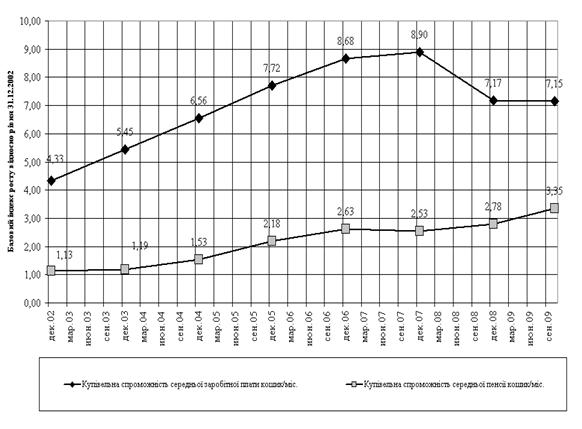
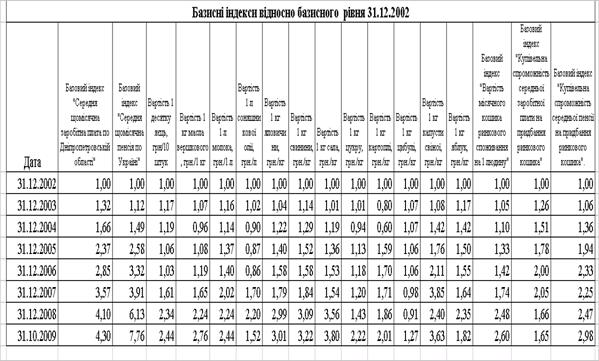
... /міс (грудень 2002) до 283,4 грн. /міс. (жовтень 2009). Таблиця 2.1 Групування результатів статистичних досліджень за 2002 - 2009 роки в таблиці абсолютних значень хронологічних рядів факторних та результативних параметрів статистичного дослідження Рис.2.1 Хронологічні ряди середньої заробітної плати, середньої пенсії та вартості „кошика" продовольчих продуктів ринка у 2002 - 2009 роках, ...
... підлітка на його статус серед однолітків. ВИСНОВОК Матеріали дійсного психолого-педагогічного дослідження дозволяють нам зробити наступні висновки про психологічні особливості неформальних лідерів у групах дітей середнього шкільного віку. 1. З 6 виявлених у групі підлітків, що мають дуже високий статус серед однолітків (неофіційні лідери) 4 дівчинки мають найбільш високі в групі показники ...
... (що убуває) порядку. Варіаційні ряди будуються на основі кількісної групувальної ознаки. Варіаційні ряди складаються з двох елементів: варіант і частот [3]. Варіанта - це окреме значення варійованої ознаки, яке він приймає у ряді розподілу. Вони можуть бути позитивними і негативними, абсолютними і відносними. Частота - це чисельність окремих варіант або кожної групи варіаційного ряду. Частоти, ...
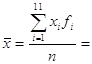
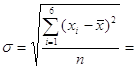



0 комментариев