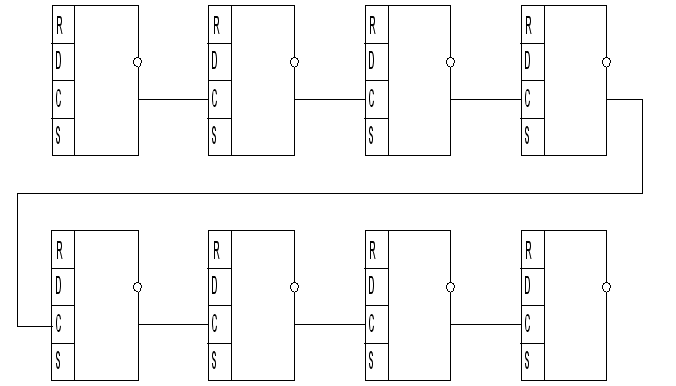
 -ми
разрядный
счётчик на
триггерах типа
D серии К155
-ми
разрядный
счётчик на
триггерах типа
D серии К155
(К155ТМ5 – 4 D-триггера)
Анализ программы на примерах
Y1 = 0 1001101 110100101110011011100011 = 0 4D D2E6E3
X1 = 1 1001011 110001100101110110100111 = 1 4B C65DA7
Выравнивание порядков:
МК: РгС>РгD (01001101>01001011) переход на МК1
MК1: сдвигаем мантиссу Х1 вправо на 4 разр. получаем 000011000110010111011010 и увел. порядок Х1 на 1 получаем 01001100 переход на МК
МК: РгС>РгD (01001101>01001100) переход на МК1
МК1: сдвигаем мантиссу Х1 вправо на 4 разр. получаем 000000001100011001011101 и увел. порядок Х1 на 1 получаем 1001101 переход на МК
МК: РгС=РгD (01001101=01001101)
Порядки выравненны.
Сложение мантисс:
ТгЗн1 ТгЗн2 переход на М3
М3:
ТгЗн1
0
РгВ = ![]() (00110010 111111110011100110100010); РгСм=РгА
+ РгВ + 1 = 01011011 110100100010000010000110;
(00110010 111111110011100110100010); РгСм=РгА
+ РгВ + 1 = 01011011 110100100010000010000110;
См[0] = 0 переход на М1
М1: РгСм [ 1 7]: = Сч1 [1 7] = 1001101;
РгСм [0] :== если Тг3н1=0 то 0;
ШИВых: = РгСм = 0 1001101 110100100010000010000110 = 0 4D D22086 ;
КОНЕЦ.
Y2 = 0 1001100 110100101110011011100011 = 0 4С D2E6E3
X2 = 0 1001101 110001100101110110100111 = 0 4D C65DA7
Выравнивание порядков:
РгD > РгС переход на МК2
МК2: сдвигаем мантиссу Y2 вправо на 4 разр. получаем 000011010010111001101110; уменьшаем порядок Х2 на 1 получаем 1001100; РгD = РгС
Порядки выравненны.
Сложение мантисс:
ТгЗн1 = ТгЗн2 См = РгА + ргВ = 00000000 110100111000110000010101; переход на М1
М1: РгСм [ 1 7]: = Сч1 [1 7] = 1001110;
РгСм [0] :== если Тг3н1=0 то 0;
ШИВых: = РгСм = 0 1001101 110100111000110000010101 = 0 4D D38C15;
КОНЕЦ.
Сложения и вычитания чисел с плавающей запятой
1. Производится выравнивание порядков чисел. Порядок меньшею (по модулю) числа принимается равным порядку большего числа, а мантисса меньшего числа сдвигается вправо на число S-ичных разрядов, равное разности порядков чисел.
2. Производится сложение (вычитание) мантисс, в результате чего получается мантисса суммы (разности).
3. Порядок результата принимается равным порядку большего числа.
4. Полученная сумма (разность) нормализуется.
Примем, что числа с плавающей запятой имеют основание порядка S = 16.
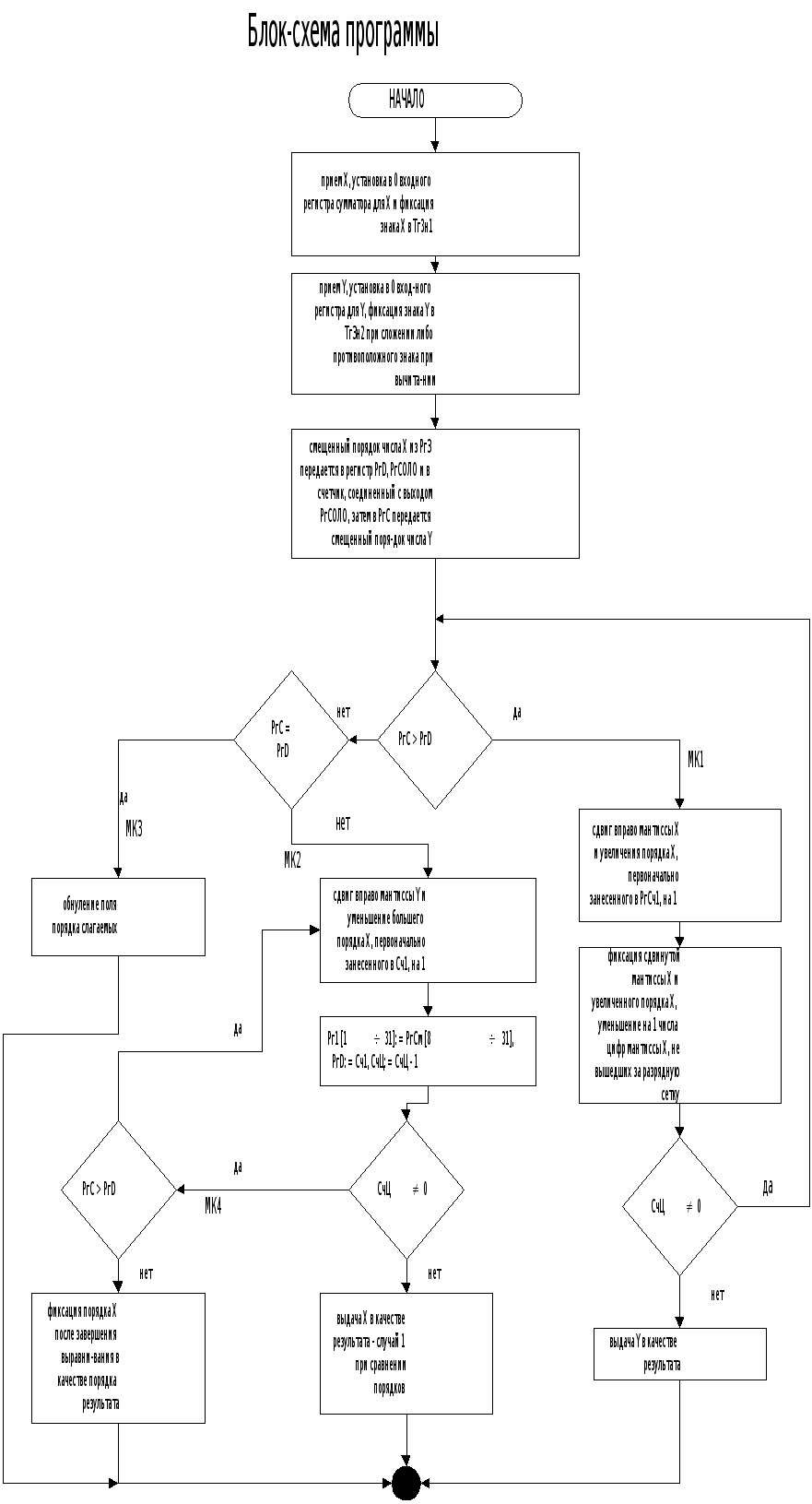
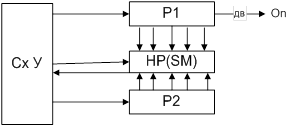
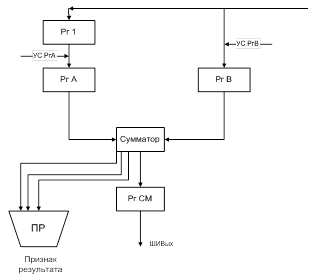
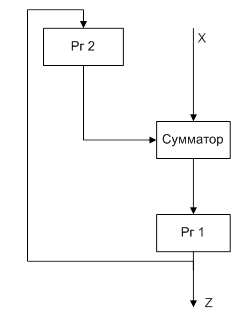
Первое слагаемое (уменьшаемое) поступает на входной регистр Рг1, второе слагаемое (вычитаемое) — на входной регистр Рг3. Знаки слагаемых хранится в триггерах знаков Тг3н1 и Тг3н2. Смещенные порядки слагаемых пересылаются в регистры РгС и РгD. Схема СОЛО применяется для сравнения и выравнивания порядков слагаемых. Сумматор См, его входные регистры РгА и РгВ и выходной регистр РгСм используются при сложении (вычитании) мантисс, а также при передаче мантисс в процедурах выравнивания порядков и нормализации результата.
Операция сложения (вычитания) может быть подразделена на следующие этапы: 1) прием операндов, 2) выравнивание порядков, 3) сложение мантисс и 4) нормализация результата.
Прием операндов описывается следующей микропрограммой:
РгЗ: = ШИВх, РгВ: = 0, Тг3н1: = Рг3[0]
< прием X, установка в 0 входного регистра сумматора для Х и фиксация знака Х в Тг3н1>;
Рг1: = ШИВых,
РгА: = 0, Тг3н2: = если
сложение то
Рг1[0]
иначе
![]() < прием
Y, установка
в 0 входного
регистра для
Y, фиксация знака
Y в ТгЗн2 при
сложении либо
противоположного
знака при вычитании
>;
< прием
Y, установка
в 0 входного
регистра для
Y, фиксация знака
Y в ТгЗн2 при
сложении либо
противоположного
знака при вычитании
>;
Выравнивание порядков начинается с их сравнения. Мантисса числа с меньшим порядком при выравнивании сдвигается вправо на число разрядов, равное разности порядков. Поскольку рассматриваемые числа с плавающей запятой имеют S = 16, сдвиг осуществляется шестнадцатеричными разрядами, т. е. каждый сдвиг производится на четыре двоичных разряда.
При сравнении порядков возможны пять случаев:
1) ![]() (m— число
разрядов мантиссы).
В качестве
результата
суммирования
сразу же может
быть взято
первое слагаемое,
так как при
выравнивании
порядков все
разряды мантиссы
второго слагаемого
принимают
нулевое значение;
(m— число
разрядов мантиссы).
В качестве
результата
суммирования
сразу же может
быть взято
первое слагаемое,
так как при
выравнивании
порядков все
разряды мантиссы
второго слагаемого
принимают
нулевое значение;
2) ![]() .
В качестве
результата
суммирования
может быть
взято второе
слагаемое;
.
В качестве
результата
суммирования
может быть
взято второе
слагаемое;
3) ![]() .
Можно приступить
к суммированию
мантисс;
.
Можно приступить
к суммированию
мантисс;
4) ![]() Мантисса
второго слагаемого
сдвигается
на
Мантисса
второго слагаемого
сдвигается
на ![]() разрядов вправо,
затем производится
суммирование
мантисс;
разрядов вправо,
затем производится
суммирование
мантисс;
5) ![]() Перед
выполнением
суммирования
мантисс производится
cдвиг
на
Перед
выполнением
суммирования
мантисс производится
cдвиг
на ![]() разрядов вправо
мантиссы первого
слагаемого.
разрядов вправо
мантиссы первого
слагаемого.
За порядок результата при выполнении суммирования принимается больший из порядков операндов.
Выравнивание порядков осуществляется следующим образом. Смещенный порядок числа Х из РгЗ передается в регистр РгD, РгСОЛО и в счетчик, соединенный с выходом РгСОЛО. Затем в РгС передается смещенный порядок числа Y:
РгС: = О, PD [0]: = 0, PгD [1 7] := Рг3 [1 7];
РгСОЛО: = РгС PгD;
Сч1: = РгСОЛО;
РгС [О]: = 0, РгС [1 7] = Pг [1 7];
После этого начинается сравнение порядков чисел Х и Y на СОЛО и сдвиг мантиссы числа с меньшим порядком вправо,
Для того чтобы учесть случаи 1 и 2, возникающие при сравнении порядков, и не делать лишних сдвигов мантиссы, превратившейся в процессе выравнивания порядков в 0, на счетчике циклов СчЦ фиксируется предельное число сдвигов, равное количеству шестнадцатеричных цифр мантиссы:
СчЦ: = 6;
При выполнении сдвига на один шестнадцатеричный разряд содержимое СчЦ уменьшается на 1. При СчЦ = 0 сдвиги прекращаются и в качестве результата берется большее слагаемое.
Микропрограмма выравнивания порядков:
| МК: | если РгС > РгD то МК1 иначе если РгС = РгD то МКЗ иначе МК2; |
| MK1: | PгB [8 31]: = PгЗ [8 31]; РгСм: = П(4) См, РгСм [0 3]: = 0, Сч1 := Сч1+1 ; Рг3[8 31]:=РгСм[8 31]; РгD:=Сч1, СчЦ: = СчЦ - 1 ; если СчЦ 0 то МК; РгВ: = 0, РгА: = Рг1, РгСм := См; ШИВых: = РгСм; конец ; |
| МК2: | РгА[8 31] :=Рг1 [8 31]; РгСм: = П (4) См, РгСм [0 3] : = 0, Сч1 := Сч1-1 ; Рг1 [1 31]: = РгСм [8 31], РгD: = Сч1, СчЦ: = СчЦ - 1, если СчЦ 0, то МК4 иначе РгА: =0, РгВ: =Рг3, РгСм: =См, ШИВых: = РгСм, конец ; |
| МК4: | если РгС > PгD то МК2; PгD[0]: = 0, РгD[1 7]: = Рг3[1 7], РгС = 0; РгСОЛО : = РгС PгD; Сч1: = РгСОЛО ; |
| МКЗ: | РгСм: = 0, Pгl [0 7] : = РгСм, РгЗ [0 7] : = РгСм ; |
После выравнивания порядков модули мантисс хранятся в Pгl и РгЗ в разрядах с 8-го по 31-й, их знаки в Тг3н2 и Тг3н1, а порядок результата в Сч1.
Сложение мантисс. Анализируются знаки мантисс и при равенстве знаков модули мантисс складываются. Если оказывается, что См [7] = 1, то возникло переполнение при сложении мантисс. В случае переполнения мантисса суммы сдвигается на четыре двоичных разряда (один шестнадцатеричный разряд) вправо, а порядок увеличивается на 1 (Сч1: = Сч1 + 1). Если после этого Сч1 [0] = 1, то формируется признак прерывания из-за переполнения порядка. Если переполнения нет, то в РгСм формируется результат операции, для чего содержимое Сч1 [1 7] заносится в РгСм [1 7], в РгСм [0] передается знак, а в РгСм [8 31]— мантисса суммы.
При различных знаках мантисс отрицательная мантисса передается на входной регистр сумматора в обратном коде и производится суммирование ее с прямым кодом положительной мантиссы и 1, прибавляемой к младшему разряду сумматора. Знак результата фиксируется в триггере знака. От полученного результата, если он отрицателен, берется его модуль. Если результат нормализован (См [8 11] 0), то на РгСм заносятся знак результата (по значению триггера знака), порядок по значению Сч1 и модуль мантиссы.
Если результат не нормализован и нет исчезновения значимости (мантисса не равна 0), производится нормализация. Мантисса результата сдвигается влево и одновременно уменьшается порядок результата (Сч1: = Сч1 - 1). При отрицательном переполнении порядка (Сч1 [0] = 1) формируется признак исчезновения порядка. Если нормализация завершается без исчезновения порядка, формируется результат операции из кода знака, порядка и мантиссы.
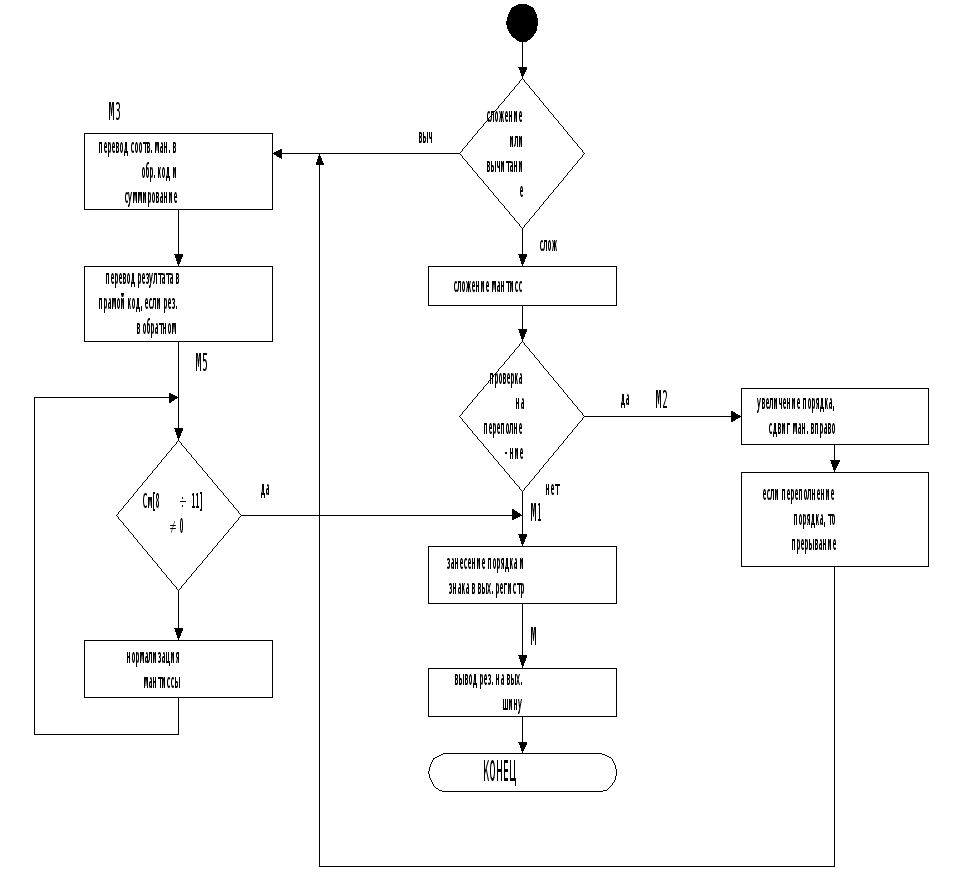
Микропрограмма процедуры сложения мантисс:
| если ТгЗн Тг3н2 то МЗ; РгА: = Рг1, РгВ: = РгЗ; РгСм: = См; если См[7] = 1 то М2; | |
| М1: | РгСм [ 1 7]: = Сч1 [1 7]; РгСм [0] :== если Тг3н1=0 то 0 иначе 1; |
| М: | ШИВых: = РгСм; конец; |
| М2: | Сч1:=Сч1+1, РгСм := П(4)См, РгСм[0 3]:=0; если Сч1[0]=0 то М1 иначе прерывание из-за переполнения порядка; |
| МЗ: | если Тг3н1=0 то РгА := РгА : = Рг1, РгВ: = РгСм :=РгА+РгВ +1; если См[0]=0 то M4; Рг3:= РгСм; РгА :=0, РгВ: = РгСм:= РгА +РгВ +1; |
| М4: | ТгЗн1 := РгЗ [0]; |
| М5: | если См [8 11] 0 то M1; если См 0 то М6; РгСм: = 0, прерывание из-за потери значимости; |
| M6: | Сч1:=Сч-1, РгСм := Л(4)См, РгСм[2831]: = 0; РгЗ: = РгСм; РгВ : = РгЗ, РгА: = 0; РгСм: = См; если Сч1[0]=0 то М5; РгСм: = 0, прерывание из-за исчезновения порядка; |
Сложение и вычитание выполняются приближенно, так как при выравнивании порядков происходит потеря младших разрядов одного из слагаемых. В этом случае погрешность всегда отрицательна и может доходить до единицы младшего разряда. Чтобы уменьшить погрешность, применяют округление результата. Для этого может быть использован дополнительный разряд сумматора, в который после выполнения суммирования добавляется 1.
5
Похожие работы
... с их сравнения. Мантисса числа с меньшим порядком при выравнивании сдвигается вправо на число разрядов, равное разности порядков. Поскольку рассматриваемые числа с плавающей запятой имеют S = 16, сдвиг осуществляется шестнадцатеричными разрядами, т. е. каждый сдвиг производится на четыре двоичных разряда. При сравнении порядков возможны пять случаев: 1) (m— число разрядов мантиссы). В качестве ...
... . 3.2.2. Деление чисел с плавающей запятой выполняется в соответствии с формулой: X S_аpx_Аgx gx --- = ------ = S_аp_АX_а-py_А --- Y S_аpy_Аgy gy . При делении чисел с плавающей запятой мантисса частного равначастному от деления мантиссы делимого на мантиссу делителя, а порядокчастного - разности порядков делимого и делителя. Частное нормализуется и ...
... систем: 1) Возможность работы в различных режимах 2) модульная структура 3) стандартизация 4) иерархия 5) адаптация 6) сервис Структура ЭВМ ВС – совокупность компонентов и связей между ними. Архитектура ЭВМ – организация ЭВМ. Функциональная классификация: 1) по назначению – универсальные и специализированные. 2) многомашинные и многопроцессорные Основная особенность – параллельная работа ...
... этих кодов операция вычитания (или алгебраического сложения) сводится к арифметическому сложению. В результате упрощаются арифметические устройства машин. Для представления двоичных чисел в машине применяют прямой, обратный и дополнительный коды. Во всех этих кодах предусматривается дополнительный разряд для представления знака числа, причем знак «+» кодируется цифрой 0, а знак « — » - цифрой 1. ...
0 комментариев