Формирование понятия призмы и умение ее видеть

I этап: Введение понятия призмы

Цель: Ввести понятие призмы (прямой, наклонной, правильной).

Оборудование: пластилиновые модели призмы, плакаты, различные модели призм.

Ученики работают группами. Перед ними на столах по одному комплекту моделей геометрических тел (призмы наклонные, прямые, с различными основаниями, конусы, цилиндры – пластиковые, пирамиды).

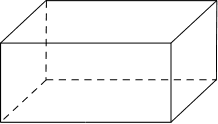
Упражнение 1: Возьмите Пластилиновый цилиндр и впишем в его основание многоугольник. Проведем через вершины многоугольника образующие и разрежем цилиндр по ним.

Проблема 1: Что из себя представляет полученная фигура?

Упражнение 2: Выберите из предложенных моделей фигуры схожие с полученной фигурой (пластилиновой).

Проблема 2: Как вы можете охарактеризовать группу выделенных фигур? Сформулируйте определение данных фигур.

В результате дискуссии с учениками, учитель корректирует определения, предложенные ими, и дает соглашение.

Соглашение 1: Если направляющая замкнутая ломаная линия, то в этом случае цилиндрическая поверхность называется призматической поверхностью.

Соглашение 2: Призмой называется цилиндр, боковая поверхность которого является частью призматической поверхности.

Соглашение 3: Сели многогранник, ограниченный замкнутой призматической поверхностью, пересеченной двумя параллельными плоскостями, то он называется призмой.

Соглашение 4: Призмой называется многогранник, который состоит из двух плоских многоугольников, лежащих в разных плоскостях и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих многоугольников.

Историческая справка: Призма: Греч. Прiσμΰ – отпиленное (тело), опилки. Античный термин Прiω (прио) – пилю.

Упражнение 3: Как еще можно подразделить эти фигуры?

Ученики замечают, что часть стоит “прямо”, “ровно”, другие “косо”, “наклонно”.

Проблема 3: Описать прямые призмы, выделить существенные свойства.

Упражнение 4: Обвести карандашом основание (на листе бумаги).

Вывод: Получился многоугольник. Выясним сколько таких равных многоугольников есть у призмы и соглашаемся называть их нижним и верхним основаниями.

Проблема 4: Равны ли основания призмы?

Упражнение 5: А теперь рассмотрим призмы и постараемся их охарактеризовать в соответствии с многоугольниками в основаниях.

Упражнение 6: Какими фигурами являются боковые грани, боковые грани прямых призм?

Вывод: Независимо от основания, грани прямых призм являются прямоугольниками.

Соглашение 5: Общую часть двух граней призмы будем называть ребром призмы, общую часть двух боковых граней призмы будем называть боковым ребром призмы.

Ученики делают вывод, что число ребер зависит от многоугольника являющегося основанием призмы, в результате чего можно сформулировать гипотезу: Если многоугольник является основанием призмы и имеет n сторон, то призма имеет 3n ребер, в том числе n боковых ребер.

Упражнение 7: Сформулируйте определение высоты призмы.

Распознавая на моделях их высоты, ученики равным образом устанавливают, что высота прямой призмы равна длине ее бокового ребра.

Упражнение 8: Сколько вершин имеют призмы, изображенные на рисунке.

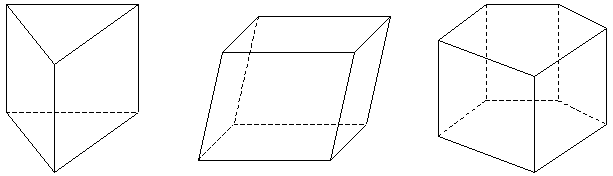
Вывод: Число вершин призмы зависит от многоугольника являющегося его основанием: если он имеет n вершин, то число его вершин равно 2n.

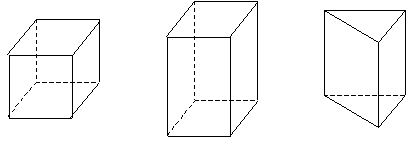
Упражнение 9: Выберите из комплекта правильные призмы.

II этап: Взаимное расположение ребер и граней призы

Цель: Сформировать понятие параллельности и перпендикулярности прямых и плоскостей.

Оборудование: модели, рисунки призм.

Сначала на моделях, затем на рисунках этих моделей учащиеся распознают и указывают параллельные, перпендикулярные, наклонные ребра, параллельные и перпендикулярные грани.

Упражнения на выявление свойства призм.

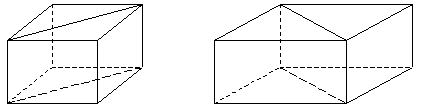
Упражнение 1: Назовите параллельные ребра и грани на призмах, изображенных на рисунке.

Упражнение 2: Отметьте все ребра и грани перпендикулярные к нижнему основанию призм, изображенных на рисунке.

Упражнение 3: Проанализируйте взаимное расположение прямых содержащих соответствующие ребра.

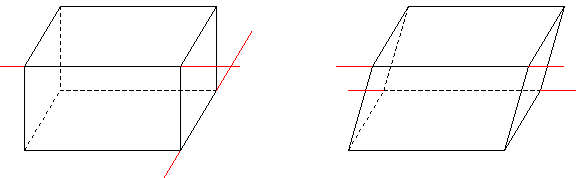
Упражнение 4:

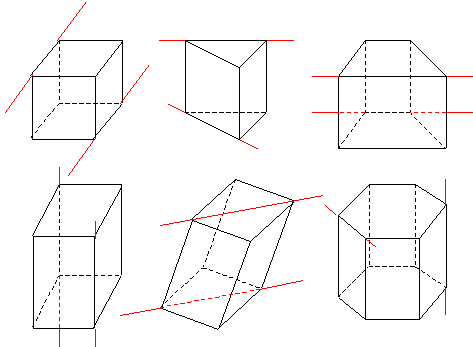
Ответьте на вопросы:

параллельны ли эти ребра? лежат ли эти ребра в одной плоскости? можно ли указать пару плоскостей, каждая из которых содержит одно из этих ребер? перпендикулярны ли эти ребра? пересекаются ли прямые, содержащие указанные ребра?

Упражнение 5: Выберете в своем наборе моделей призм, призмы изображенные а рисунке. Покажите на каждой из выбранной модели ребра, пересекающиеся с ребрами, отмеченными на рисунке. Покажите еще одну пару ребер, которые не лежат в одной плоскости и не являются ни параллельными, ни перпендикулярными.

Вывод: В результате второго этапа отработанного визуальное представление призмы и отработаны у учащихся понятия параллельности, перпендикулярности прямой и плоскости в пространстве.

III этап: Введение понятия развертки призмы (поверхности)

Цель: Расширение знаний учащихся связанных с общим понятием призмы. Ввести понятие развертки (опираясь на понятие развертки прямого параллелепипеда на уроках черчения, труда).

Оборудование: Картонные модели призм, ножницы, раскладные модели призм.

Перед учениками на партах находятся картонные модели призм.

Упражнение 1: Разрежьте взятую модель призмы по некоторым ребрам так, чтобы получилась фигура, которую можно разложить на плоскости (на парте).

Проблема 1: Что вы понимаете под разверткой?

Соглашение 1: Под разверткой будем понимать плоское изображение всех граней, соединенных между собой ребрами.

Упражнение 2: Объединение каких многоугольников является фигура, полученная как развертка призмы?

Ученики устанавливают, что развертка призмы является объединением всех ее граней.

Соглашение 2: Плоскую фигуру, являющуюся объединением всех боковых граней и оснований призмы, будем называть разверткой призмы.

Упражнение 3: Представьте мысленно, как могут выглядеть развертки данной модели призмы. Нарисуйте эти развертки, вырежьте их и склейте из нее модель призмы, выделив необходимые сгибы.

Упражнение 4: Постройте хотя бы еще одну развертку той самой призмы, две развертки которой изображены на рисунках.

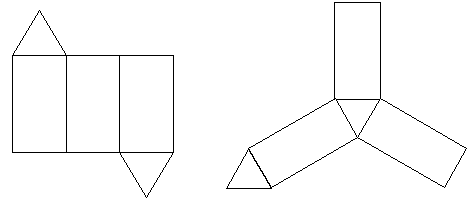
После этих упражнений понятие развертки и поверхности следует систематизировать.

Упражнение 5: Объясните связь рисунков (2) и (3) с призмой (1).

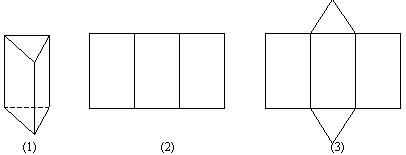
После этого упражнения ученики выявляют полную и боковую развертки.

Упражнение 6: Построить полные и боковые развертки следующих призм:

IV этап: Введение понятия площади поверхности призмы

Цель: Углубление и расширение понятий площади поверхности на наглядно интуитивной основе.

Оборудование: модели призм.

Каждый ученик выбирает модель над которой будет выполнять следующие упражнения, которое позволит выяснить степень усвоения понятия развертки призмы.

Упражнение 1: Постройте развертку выбранной призмы. Выясните, есть ли равные многогранники в развертке, если есть то зарисуйте их.

Проблема 1: Как вычислить площадь поверхности развертки призмы?

Используя знания приобретенные ранее учащиеся убеждаются, что развертка призмы является объединением всех его граней, причем некоторые из граней равны друг другу.

Проблема 2: Как вычислить полную площадь поверхности призмы?

Соглашение 1: Площадью полной поверхности призмы называют сумму площадей всех граней призмы (Sп).

Соглашение 2: Площадью боковой поверхности призмы называется сумма площадей ее боковых граней (Sб)

Sп = Sб + 2 SоснSб = S1 + S2 + …

Упражнение 2: Поменяйте себе модель призмы, и вычислите боковую и полную ее поверхность.

Итог: Обобщим с помощью учащихся сведения о полной поверхности призмы и боковой поверхности призмы.

V этап: Введение понятия объема призмы

Цель: Углубить у учащихся интуитивно-наглядное понятие объема пространственных фигур.

Оборудование: модели призм.

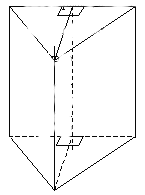
Разрежьте (пластилиновую модель призмы, плоскостью проходящей через диагональ основания. Какие получили фигуры?

В результате выполнения этого упражнения ученики получили две призмы с равными основаниями (основанием является прямоугольный треугольник), а все остальные соответствующие элементы призмы равны.

Упражнение 2: Как вычислить объем каждой из полученных призм?

Вывод: Каждая из полученных призм имеет объем равный половине объема данного параллелепипеда. (Объем параллелепипеда умеют вычислять в пятом классе).

Упражнение 3:

Дана призма, в основании которой треугольник. Как вычислить объем этой призмы?

Учащиеся умеют вычислять объем призмы основанием которой является прямоугольный треугольник.

Важно, чтобы учащиеся увидели в этом упражнении предыдущее. Объем данной призмы есть сумма объемов двух призм, основаниями которых являются прямоугольные треугольники.

Затем предлагается вычислить объем призмы основание которой трапеция, или любой другой произвольной формы.

V = Sосн h

Сборник задач

Задача 1: Запомните пропуски.

В правильной треугольной призме сторона основания равна a, боковое ребро 2a. Найти площадь сечения, проведенного через сторону одного и центр другого основания.

Дано:

АВСА1В1С1 – произвольная призма

АВ = а

АА1 = 2а

Sсеч = ?

Решение:

1) Плоскость сечения α определяют прямая … и точка …; проведем сечение.

2) ВС ׀׀ В1С1, значит …

3) α ΒС ׀׀ А1В1С1, значит, линия пересечения В2С2 …

4) секущая плоскость α θмеет с гранью АА1В1В две общие точки В и В2, значит …; а с гранью АА1С1С – точки С и С2, значит …;

5) сечение ВВ2С2С – …, т.к. …;

6) находим высоту О1D трапеции ВВ2С2С, ОD ┴ ВС

7) О1D┴ …

8) ; ВС = а

9) В2С2 = ?; Δ ΐ1В2С2 …

10) = …

11) = … (медиана в точке пересечения …)

12) = …; = ….

13) Из ΔОО1D: О1D2= … + … (…)

14) АD = a sin … = … ; OD = 1/3 … = …;

15) О1D2 = … = … = …; О1D = … = …

16) Scеч =

Задача 2: В прямоугольной призме стороны основания равны 5 см, 6 см, 7 см, сечение проведенное через среднюю сторону одного основания и противоположную вершину другого, составляет с основанием угол в 60о. Найти площадь полной поверхности призмы.

Решение: Sп = Sб + 2 Sосн (1)

1) Sб = ? Sб = Р l (2), Р = … + … +… = …; 2) из ΔADA1 имеем l = AD … (3);

3) AD - высота ΔAВС, (4);

4) , а = 5 см, b = 6 см, c = … p = Ѕ … = …

5) подставим в (4) найденное значение S и ВС: , АD = …

6) подставим в (3) значение AD и tg 60о: l = … = …; 7) подставим в (2) значения P и l: Sб = … = …; 8) подставим в (1) значения Sб и Sосн: Sп = … + … ≈ … .

Задача 3: В прямоугольном параллелепипеде сторона основания равна а и составляет с диагональю основания угол α, а с диагональю грани, которой принадлежит сторона, угол β. Найти площадь боковой поверхности.

Решение: 1) Sб = Р l (2), 2) Р = 2 ( … + … ); AD = а; 3) АВ = ? из ΔAВD имеем АВ = … =… (катет равен …); 4) Р = 2 (…+…) = … = … = … = … 5) l = ? из ΔAА1D имеем AА1 = АD…=…; 6) Sб = … = … .

1) Будет ли сечение, перпендикулярное к боковому ребру призмы, перпендикулярно к ее боковой грани?

2) Боковое ребро призмы образует равные острые углы с прилежащими сторонами основания. Что следует сказать о проекции этого ребра на плоскость основания?

3) Показать на чертеже расстояние ребра куба от пересекающейся с ним диагоналями куба.

4) Показать в кубе расстояние между а) диагональю основания и перпендикулярной к ней диагональю куба; б) непересекающимися диагоналями непересекающихся граней.

Задача 4: Основанием призмы служит правильный ΔAВС со стороной а, вершина А1 проецируется в центр нижнего основания и ребро АА1 составляет со стороной снования АВ угол 45о. Найти объем.