Центральная предельная теорема и ее доказательство через ряды Тейлора

6251

знак

таблиц

изображений

Прежде чем приступить к рассмотрению центральной предельной теоремы, я считаю нужным сказать о слабой сходимости.

Пусть задана последовательность случайных величин (далее с. в.) $\{\xi_n\}$ , задано некоторое распределение $\cal F$ с функцией распределения $F_\xi$ и $\xi$ — произвольная с. в., имеющая распределение $\cal F$ .

Определение.

Говорят, что последовательность с. в. $\{\xi_n\}$ при $n\to\infty$ сходится слабо или по распределению к с. в. $\xi$ и пишут: $\xi_n\Rightarrow\xi$ , или $F_{\xi_n}\Rightarrow F_\xi$ , или $\xi_n\mbox{ $\Rightarrow$\space }\cal F$ ,
если для любого такого, что функция распределения $F_\xi$ непрерывна в точке , имеет место сходимость $F_{\xi_n}(x)\to F_\xi(x)$ при $n\to\infty$ .

Иначе говоря, слабая сходимость — это поточечная сходимость функций распределения во всех точках непрерывности предельной функции распределения.

Свойство 1.

Если $\xi_n\Rightarrow\xi$ , и функция распределения $F_\xi$ непрерывна в точках и , то

$\mathsf P(\xi_n\in[a,b])\to
\mathsf P(\xi\in[a,b])$ и т.д. (продолжить ряд).

Наоборот, если во всех точках и непрерывности функции распределения $F_\xi$ имеет место, например, сходимость $\mathsf P(\xi_n\in[a,b])\to
\mathsf P(\xi\in[a,b])$ , то $\xi_n\Rightarrow\xi$ .

Следующее важное свойство уточняет отношения между сходимостями.

Свойство 2.

1. Если $\xi_n\buildrel {\rm p} \over \longrightarrow\xi$ , то $\xi_n\Rightarrow\xi$ .

2. Если $\xi_n\Rightarrow c=\text{const}$ , то $\xi_n\buildrel {\rm p} \over \longrightarrow c$ .

Свойство 3.

1. Если $\xi_n\buildrel {\rm p} \over \longrightarrow c=\text{const}$ и $\eta_n\Rightarrow\eta$ , то $\xi_n\cdot\eta_n\Rightarrow c\eta$ .

2. Если $\xi_n\buildrel {\rm p} \over \longrightarrow c=\text{const}$ и $\eta_n\Rightarrow\eta$ , то $\xi_n+\eta_n\Rightarrow c+\eta$ .

Несколько содержательных примеров слабой сходимости я рассмотрю ниже. Но основной источник слабо сходящихся последовательностей и необычайно мощное и универсальное средство для асимптотического анализа распределений сумм независимых и одинаково распределенных случайных величин предоставляет нам центральная предельная теорема.

Я буду называть следующее утверждение «ЦПТ Ляпунова» (А. М. Ляпунов: 1901), но сформулирую и докажу теорему Ляпунова только в частном случае, т.е. для последовательности независимых и одинаково распределенных случайных величин.

Центральная предельная теорема.

Пусть $\xi_1,\xi_2,\ldots$ — независимые и одинаково распределенные случайные величины с конечной и ненулевой дисперсией: $0<\mathsf D\,\xi_1\ <\infty$ . Обозначим через сумму первых случайных величин: $S_n=\xi_1+\ldots+\xi_n$ .

Тогда последовательность случайных величин $\dfrac{S_n-n\,\mathsf E\,\xi_1}{\sqrt{n\,\mathsf D\,\xi_1}}$ слабо сходится к стандартному нормальному распределению.

Доказательство.

Пусть $\xi_1,\xi_2,\ldots$ — последовательность независимых и одинаково распределенных случайных величин с конечной и ненулевой дисперсией. Обозначим через математическое ожидание $\mathsf E\xi_1$ и через $\sigma^2$ — дисперсию $\mathsf D\xi_1$ . Требуется доказать, что

$\begin{displaymath}
\dfrac{S_n-na}{\sigma\sqrt{n}}=
\dfrac{\xi_1+\dots+\xi_n-na}{\sigma\sqrt{n}}\mbox{ $\Rightarrow$\space }\mathbf N_{0,1}.\end{displaymath}$

Введем стандартизированные случайные величины $\zeta_i=\dfrac{\xi_i-a}{\sigma}$ — независимые с.в. с нулевыми математическими ожиданиями и единичными дисперсиями. Пусть есть их сумма $Z_n=\zeta_1+\dots+\zeta_n=(S_n-na)/\sigma$ . Требуется доказать, что

$\begin{displaymath}
\dfrac{Z_n}{\sqrt{n}}\mbox{ $\Rightarrow$\space }\mathbf N_{0,1}.\end{displaymath}$

Характеристическая функция величины ${Z_n}/{\sqrt{n}}$ равна

$\begin{equation}
\varphi_{Z_n/\sqrt{n}}(t)
\,
{\buildrel{{\boldsymbol{\varphi3}}...
 ...\left(\varphi_{\zeta_1}\left(\dfrac{t}{\sqrt{n}}\right)\right)}^n.\end{equation}$

Характеристическую функцию с.в. $\zeta_1$ можно разложить в ряд Тейлора, в коэффициентах которого использовать известные моменты $\mathsf E\zeta_1=0$ , $\mathsf E{\zeta_1}^2=\mathsf D\zeta_1=1$ . Получим

$\begin{displaymath}
\varphi_{\zeta_1}(t)
\,
{\buildrel{{\boldsymbol{\varphi6}}}\...
 ...t^2}{2}\,
\mathsf E{\zeta_1}^2 +o(t^2)=1-\dfrac{t^2}{2}+o(t^2).\end{displaymath}$

Подставим это разложение, взятое в точке $t/\sqrt{n}$ , в равенство и устремим к бесконечности. Еще раз воспользуемся замечательным пределом:

$\begin{displaymath}
\varphi_{Z_n/\sqrt{n}}(t)=
{\left(\varphi_{\zeta_1}\left(\df...
 ...t\{-\dfrac{t^2}{2}\right\} \quad \text{ при } \quad n\to\infty.\end{displaymath}$

В пределе получили характеристическую функцию стандартного нормального закона. По теореме о непрерывном соответствии можно сделать вывод о слабой сходимости :

$\begin{displaymath}
\dfrac{Z_n}{\sqrt{n}}=\dfrac{S_n-na}{\sigma\sqrt{n}}
\mbox{ $\Rightarrow$\space }\mathbf N_{0,1}\end{displaymath}$

распределений стандартизованных сумм к стандартному нормальному распределению, что и утверждается в ЦПТ.

Пользуясь определением и свойствами слабой сходимости, и заметив, что функция распределения $\Phi_{a,\sigma^2}(x)$ любого нормального закона непрерывна всюду на $\mathbb R$ , утверждение ЦПТ можно сформулировать любым из следующих способов:

Следствие.

Пусть $\xi_1,\xi_2,\ldots$ — независимые и одинаково распределенные случайные величины с конечной и ненулевой дисперсией. Следующие утверждения эквивалентны друг другу и равносильны утверждению ЦПТ.

· Для любых вещественных при $n\to\infty$ имеет место сходимость

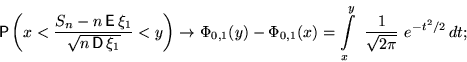
$\begin{displaymath}
\mathsf P \left(x<\dfrac{S_n-n\,\mathsf E\,\xi_1}{\sqrt{n\,\...
 ...0,1}(x)=
\int\limits_x^y ~\frac{1}{\sqrt{2\pi}}~e^{-t^2/2}\,dt;\end{displaymath}$

· Для любых вещественных при $n\to\infty$ имеет место сходимость

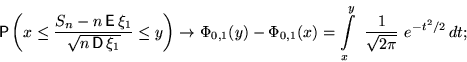
$\begin{displaymath}
\mathsf P \left(x\le\dfrac{S_n-n\,\mathsf E\,\xi_1}{\sqrt{n\...
 ...0,1}(x)=
\int\limits_x^y ~\frac{1}{\sqrt{2\pi}}~e^{-t^2/2}\,dt;\end{displaymath}$

· Для любых вещественных при $n\to\infty$ имеет место сходимость

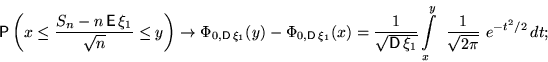
$\begin{displaymath}
\mathsf P \left(x\le\dfrac{S_n-n\,\mathsf E\,\xi_1}{\sqrt{n}...
 ...,\xi_1}}
\int\limits_x^y ~\frac{1}{\sqrt{2\pi}}~e^{-t^2/2}\,dt;\end{displaymath}$

· Если $\eta$ — произвольная с. в. со стандартным нормальным распределением, то

$\begin{displaymath}
\dfrac{S_n-n\,\mathsf E\,\xi_1}{\sqrt{n\,\mathsf D\,\xi_1}}\...
 ...subset$}$\!\!\!\!\! =$\space }{\mathbf N}_{0,\mathsf D\,\xi_1}.\end{displaymath}$

Следствием из ЦПТ является предельная теорема Муавра-Лапласа.

Предельная теорема Муавра — Лапласа.

Пусть — событие, которое может произойти в любом из независимых испытаний с одной и той же вероятностью $p=\mathsf P(A)$ . Пусть $\nu_n(A)$ — число осуществлений события в испытаниях. Тогда $\dfrac{\nu_n(A)-np}{\sqrt{np(1-p)}}\mbox{ $\Rightarrow$\space }
\mathbf N_{0,1}$ .

Иначе говоря, для любых вещественных при $n\to\infty$ имеет место сходимость

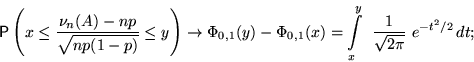
$\begin{displaymath}
\mathsf P \left(x\le\dfrac{\nu_n(A)-np}{\sqrt{np(1-p)}}
\le ...
 ...0,1}(x)=
\int\limits_x^y ~\frac{1}{\sqrt{2\pi}}~e^{-t^2/2}\,dt;\end{displaymath}$

Доказательство.

По-прежнему $\nu_n(A)$ есть сумма независимых, одинаково распределенных с. в., имеющих распределение Бернулли с параметром, равным вероятности успеха $p=\mathsf P(A)$ :

$\begin{displaymath}
\nu_n(A)=\xi_1+\dots+\xi_n, \quad \xi_i=I_i(A)=\begin{cases}...
 ... } A \text{ не произошло в } i-\text{м испытании}; \end{cases} \end{displaymath}$

Осталось воспользоваться ЦПТ.

Ниже я рассмотрю примеры использования ЦПТ.

Пример 1.

З а д а ч а. Монета подбрасывается 10000 раз. Оценить вероятность того, что частота выпадения герба отличается от вероятности более чем на одну сотую.

Р е ш е н и е. Требуется найти $\mathsf P\left(\left\vert\dfrac{\nu_n}{n}-\dfrac12\right\vert\gt{,}01\right)$ , где $n={10}^4$ , $\nu_n=\sum_{i=1}^n\xi_i=S_n$ — число выпадений герба, а $\xi_i$ — независимые с. в., имеющие одно и то же распределение Бернулли с параметром 1/2. Домножим обе части неравенства под знаком вероятности на $\sqrt{n}=100$ и поделим на корень из дисперсии $\sqrt{\mathsf D\,\xi_1}=1/2$ одного слагаемого.

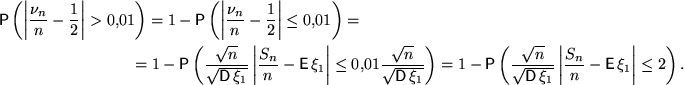
$\begin{multline*}
\mathsf P\left(\left\vert\dfrac{\nu_n}{n}-\dfrac12\right\vert\...
 ...\left\vert\dfrac{S_n}{n}-\mathsf E\,\xi_1\right\vert\le 2\right).\end{multline*}$

Согласно ЦПТ или предельной теореме Муавра — Лапласа, последовательность

$\begin{displaymath}
\dfrac{\sqrt{n}}{\sqrt{\mathsf D\,\xi_1}}
\left(\dfrac{S_n}{...
 ...t)=
\dfrac{S_n-n\,\mathsf E\,\xi_1}{\sqrt{n\,\mathsf D\,\xi_1}}\end{displaymath}$

слабо сходится к стандартному нормальному распределению. Рассмотрим произвольную с. в. $\eta$ , имеющую распределение ${\mathbf N}_{0,1}$ .

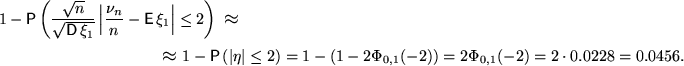
$\begin{multline*}
1-\mathsf P\left(\dfrac{\sqrt{n}}{\sqrt{\mathsf D\,\xi_1}}
\le...
 ...=1-(1-2\Phi_{0,1}(-2))=2\Phi_{0,1}(-2)
=2\cdot 0{.}0228=0{.}0456.\end{multline*}$

Пример 2.

Прекрасным примером ЦПТ в экономике может служить ее использование в страховом деле. В большинстве случаев конкретный вид распределения потерь (размеров отдельных требований о выплате страховых сумм) не играет существенной роли, поскольку сумма исков, предъявляемых страховщику (величина суммарного иска), обычно зависит только от средней величины и дисперсии убытка. Дело в том, что если количество страховых случаев значительно превышает единицу, то в силу центральной предельной теоремы распределение суммарного иска является нормальным распределением. Обозначив его дисперсию как D_Z, а математическое ожидание (среднее значение суммарного иска) как <Z> = <N><Q>

- где <N>, <Q> - среднее значение числа страховых случаев и величины страховой выплаты, получаем следующее выражение для рисковой надбавки Т_r:

Т_r = [(Т₀*a)/(<N>*<Q>)]*(<N>*D_Q + <Q>²*D_N)^0.5

- где D_Q и D_N -дисперсии величины страховой выплаты и количества страховых случаев.

В простейшем случае, когда все выплаты одинаковы (а, следовательно, их дисперсия равна нулю), имеем:

Т_r = (Т₀*a)/N^0.5

Эта формула также дает неплохое приближение, если коэффициент вариации уровня страховых выплат значительно меньше единицы.

При включении в страховой полис нескольких независимых рисков ожидаемая величина страховых выплат в соответствии с теоремой о сложении вероятностей представляет собой сумму ожидаемых страховых выплат по каждому риску в отдельности, а рисковая надбавка вычисляется как среднеквадратичная величина всех рисковых надбавок.

Раздел: Математика
Количество знаков с пробелами: 6251
Количество таблиц: 0
Количество изображений: 0

Скачать

... И. Европоцентризм и русское национальное самосознание // Социологические исследования. 1996. № 2. С. 55–62. 24. Зиммель Г. Экскурс по проблеме: как возможно общество? // Вопросы социологии. 1993. Т. 2. № 3. С 16-26. 25. Иванов В.Н. Реформы и будущее России // Социологические исследования. 1996. № 3. С. 21-27. 26. Капусткина Е.В. Социальные реформы в России: история, современное ...

Скачать

... М. В. Неоклассическая модель чистой монополии. М.: ИМЭМО, АН СССР, 1990. 3. Лейбенстайн X. Аллокативная эффективность в сравнении с "Х-эффективностью" // Теория фирмы. С. 477—506. 4. Маленво Э. Лекции... Гл. III. § 9. С. 80—85. 5. Робинсон Дж. Экономическая теория... Гл. 3—5. С. 88—130. 6. Стиглер Дж. Совершенная конкуренция: исторический ракурс // Теория фирмы. С. 299—328. 7. Самуэльсон П. ...

Скачать

... Доказать: По определению второй смешанной производной. Найдем по двумерной плотности одномерные плотности случайных величин X и Y. Т.к. полученное равенство верно для всех х, то подинтегральные выражение аналогично В математической теории вероятности вводится как базовая формула (1) ибо предлагается, что плотность вероятности как аналитическая функция может не существовать. Но т.к. в нашем ...

Скачать

... поколений. Естественно, особенно они заметны, если популяция находится в изоляции, т.е. отсутствует миграция генов извне. Известны сообщества такого рода в человеческом обществе. Часть 2 Математические модели нейронных систем Изучение нейронных систем -одно из самых романтических направлений научных исследований, поскольку нейронные системы присущи как человеку, так и животным. Самая ...

Главная Новости Рефераты Статьи Вузы

О проекте Соглашение

Наверх

Войти на сайт

Навигация

Похожие работы

0 комментариев

Разделы

Инфо

Следите за новостями