Приложение 1: Описание программы
Приложение 2: Текст программы
1. ОБЩАЯ ПОСТАНОВКА ЗАДАЧИПеренос тепла (или вещества) теплопроводностью (для вещества соответственно диффузией) и конвекцией описывается дифференциальным уравнением параболического типа:
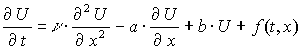( 1 )
где 
температура (или концентрация). Пусть 
являются некоторыми константами и 
. Уравнение (1) при указанных выше предположениях называется модельным уравнением диссипации, конвекции и кинетики. Слагаемые правой части имеют следующий физический смысл:
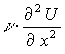- соответствует переносу тепла теплопроводностью (или вещества диффузией);
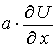- соответствует конвективному переносу;-
- "кинетический член", соответствует источнику, пропорционально-
му температуре или концентрации;
- интенсивность внешних источников или стоков.
В дальнейшем будем рассматривать только тепловую интерпретацию уравнения (1).
Численное решение уравнения (1) будем искать в области 
:
( 2 )
при заданных начальных значениях температуры: 
( 3 )
и граничных условиях.
Граничные условия описывают режимы теплообмена с внешней средой:
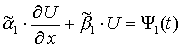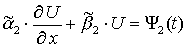при 
;
при 
.
В качестве тестовых задач для температуры 
мною были выбраны следующие пять функций:
( 9 )
( 10 )
( 11 )
( 12 )
( 13 )
Для функции (9) имеем: 
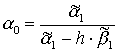
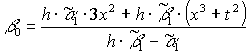
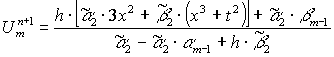
Для функции (10):
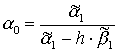
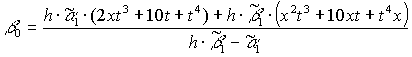
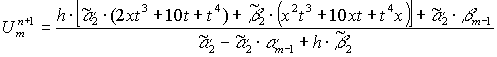
Для функции (11):
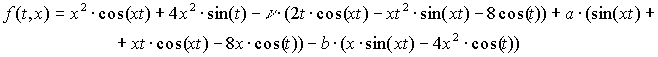
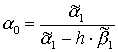
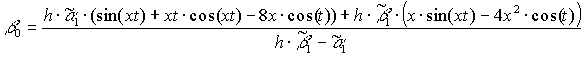
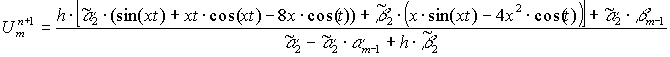
Для функции (12): 
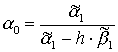
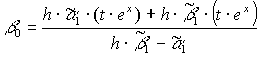
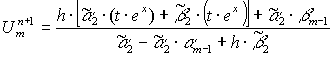
Для функции (13): 
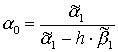
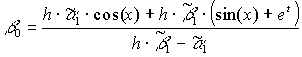
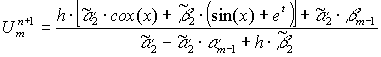
Данные функции тестировались на отрезке по X: [0, 1], по времени: [0, 1], с количеством разбиений по этим отрезкам - 30.
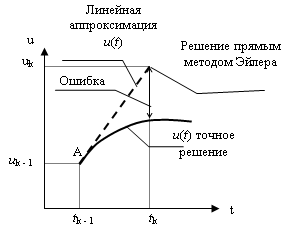
3. МЕТОДИКА РЕШЕНИЯ ТЕСТОВЫХ ЗАДАЧДанная задача решается с помощью двухслойной неявно конечно-разностной схемы.
Схема реализуется в три этапа.
1 этап: находятся предварительные значения 
с помощью 4-х точечной неявной схемы:
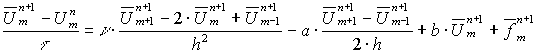( 5 )
2 этап: используется за два шага. Сначала находятся 
на полученном слое (
) с шагом 
, а затем 
через . В этом случае используется 4-х точечная неявная разностная схема:
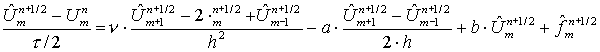( 6 )
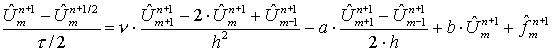( 7 )
3 этап: окончательные значения 
находятся в виде линейной комбинации двух предварительных значений:
( 8 )
Для решения (1) воспользуемся формулами (5) - (8). Данные уравнения представляют трех диагональные матрицы, решаемые методом скалярной прогонки.
В начале нужно преобразовать (5) – (7) к виду:
( 14 )
Тогда (5) примет вид:
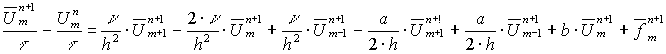
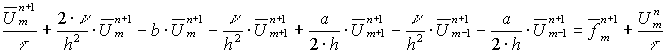
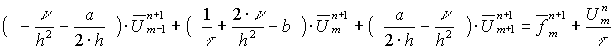
Т.е. 
;
;
;
.
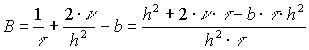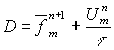Формула (6) преобразуется в:
Т.е. 
;
;
;
.
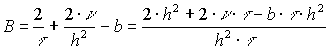Формула (7) преобразуется в:
Т.е. 
;
;
;
.
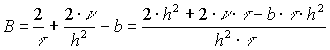Далее решаем по формулам скалярной прогонки:
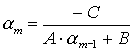
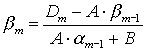( 15 )
( 16 )
Для определения 
, 
и 
воспользуемся данными граничными условиями, т.е. формулой (4) и функцией 
. Так если мы берём из формулы (9), то имеем:
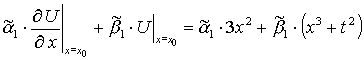
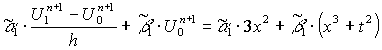
Приведём это выражение к виду: 
.
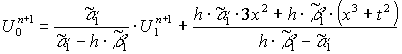
Т.е. теперь мы имеем и :
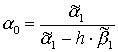
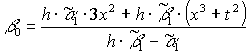
Далее найдем конечное : 
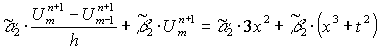
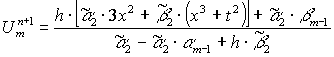( 18 )
Проведя аналогичные расчёты для заданных формулами (10) – (13), мы получим соответствующие 
, 
и 
. Далее мы можем решить системы методом прогонки и получить требуемый результат.
В результате проведённых испытаний программа показала свою высокую надёжность. Были получены следующие данные.
При расчёте с использованием функции 
и входных данных 
; 
; 
; 
; 
; 
; 
на отрезке по X и по времени [0,1] с шагом 0,033 был получен результат с ошибкой равной 0,0675.
Для функции 
при 
; 
; 
; 
; 
; 
; 
, на том же промежутке, ошибка составляет 0,055.
С функцией и 
; 
; 
; 
; 
; 
; 
ошибка примет значение 0,0435.
При и условиях 
; 
; ; ; ; ; в результате возникает ошибка равная 0,0055.
И, наконец, если выбрана функция и 
; 
; 
; 
; 
; 
; 
, то ошибка составит 0,00255.
Т.е. можно сказать, что мы имеем результат с первым порядком точности. Столь малую точность можно объяснить тем, что производная, найденная при граничных условиях, так же имеет первый порядок точности.
СПИСОК ЛИТЕРАТУРЫ А. Епанешников, В. Епанешников Программирование в среде Turbo-Pascal 7.0. - М.: Диалог - Мифи, 1996. - 288 с. Петухова Т. П., Сибирцев В. В. Пакет прикладных программ для численного моделирования процессов тепло- и массопереноса. – Караганда: Изд-во КарГУ. 1993 Фигурнов В. Э. IBM PC для пользователя. - М.: Инфра - М, 1995. - 432 с. Приложение 1 ОПИСАНИЕ ПРОГРАММЫПоставленная задача была программно реализована на языке программирования Turbo-Pascal 7.0.
В состав программы входят следующие файлы:
basis.pas - PAS-файл основной части программы
(решение системы уравнений методом скалярной прогонки);
basis.v&v - EXE-файл основной части программы (вызывается из START.PAS);
fun.bmp - BMP-фаил с изображением функций;
inform.v&v - TXT-фаил с информацией о программе (вызывается из START.PAS);
music.v&v - музыкальный EXE-фаил (вызывается из START.PAS);
my_menu.pas - UNIT для создания меню;
sea.exe - программа для просмотра графических файлов;
start.pas - файл для запуска всей программы;
u - файл с результатами работы;
zastavka.v&v - EXE-фаил с заставкой к основной программе
(вызывается из START.PAS).
Файл START является, как бы оболочкой программы, из которой вызываются другие файлы. Сам процесс решения содержится в файле BASIS.
BASIS содержит следующие процедуры и функции:
Function Fun_U (Xm,t:real):real;
Вход: значение по X и значение по времени t, а также глобальная переменная выбранной
функции SelectFunction.
Действие: вычисляет точное значение функции U при заданных X и t.
Выход: Fun_U – значение функции.
Function Fun_F (Xm,t,a,b,v:real):real;
Вход: значение по X, по времени t, коэффициенты 
, 
, 
и номер выбранной функции
SelectFunction.
Действие: вычисляет значение функции F при заданных X, t, , , .
Выход: Fun_F – значение функции F.
Function Betta_Zero (time:real): real;
Вход: значение времени t и глобальные коэффициенты 
, 
, 
, номер выбранной
функции SelectFunction.
Действие: вычисляет 
, используемое в методе скалярной прогонки.
Выход: Betta_Zero – значение .
Function U_End (time,Alf,Bet:real): real;
Вход: значение времени t, 
, 
и глобальные коэффициенты 
, 
, 
, номер выбран-
ной функции SelectFunction.
Действие: вычисляет 
используемое в методе скалярной прогонки.
Выход: U_End – значение .
Procedure PrintArray;
Вход: использует глобальный массив данных U_m.
Действие: выдает содержимое U_m на экран и в файл.
Выход: вывод U_m.
Приложение 2 ТЕКСТ ПРОГРАММЫОсновная часть программы выглядит так:
Program Basis;
Uses Crt; { Подключение библиотек }
Label Metka1,Metka2; { Метки }
Var
a, b, v : real; { Коэффициенты, задаются пользователем }
h, tau : real; { Шаг по X и по времени соответственно }
X,x0 : real; { Конечное и начальное значение X }
m,n,k : word; { Переменные используемые в циклах для расчета }
T,t0 : real; { Конечное и начальное значение времени }
Kol_voX, Kol_voT : word; { Количество разбиений по X и по времени }
U_m,U_,_U_1_2,_U_1 : array [0..200] of real; { Массивы результатов }
z : array [0..200] of real; { Массив точных решений }
Xm : real; { Промежуточный X }
Alfa,Betta : array [0..200] of real; { Массив коэффициентов используемых при скалярной прогонке }
a_progonka, b_progonka, c_progonka, d_progonka : real; { Коэффициенты для скалярной прогонки }
Error : real; { Значение ошибки }
time : real; { Переменная времени }
ch : char; { Код нажатой клавиши }
SelectFunction:word; { Номер выбранной функции }
U : text; { Переменная для вывода результата в файл }
Alfa_1,Alfa_2,Betta_1,Betta_2 : real; { Коэффициенты граничных условий }
Data : word; { Переменная режима ввода начальных данных }
Function Fun_U (Xm,t:real):real; { Функция U (точное решение) }
begin
If SelectFunction=1 then Fun_U:=SQR(Xm)*Xm+SQR(t);
If SelectFunction=2 then Fun_U:=SQR(Xm)*SQR(t)*t+10*Xm*t+SQR(SQR(t))*Xm;
If SelectFunction=3 then Fun_U:=Xm*SIN(Xm*t)-4*SQR(Xm)*COS(t);
If SelectFunction=4 then Fun_U:=t*EXP(Xm);
If SelectFunction=5 then Fun_U:=SIN(Xm)+EXP(t);
end;
Function Fun_F (Xm,t,a,b,v:real):real; { Функция F }
begin
if SelectFunction=1 then Fun_F:=2*t-v*6*Xm+a*3*SQR(Xm)-b*(SQR(Xm)*Xm+SQR(t));
if SelectFunction=2 then Fun_F:=3*SQR(Xm)*SQR(t)+10*Xm+4*SQR(t)*t*Xm-v*2*SQR(t)*t+
a*(2*Xm*SQR(t)*t+10*t+SQR(SQR(t)))-b*(SQR(Xm)*SQR(t)*t+10*Xm*t+Xm*SQR(SQR(t)));
if SelectFunction=3 then Fun_F:=SQR(Xm)*COS(Xm*t)+4*SQR(Xm)*SIN(t)-v*(2*COS(Xm*t)*t-
Xm*SIN(Xm*t)*SQR(t)-8*COS(t))+a*(SIN(Xm*t)+Xm*t*COS(Xm*t)-8*COS(t)*Xm)-
b*(Xm*SIN(Xm*t)-4*SQR(Xm)*COS(t));
if SelectFunction=4 then Fun_F:=EXP(Xm)-v*(t*EXP(Xm))+a*(t*EXP(Xm))-b*(t*EXP(Xm));
if SelectFunction=5 then Fun_F:=EXP(t)-v*(-SIN(Xm))+a*(COS(Xm))-b*(SIN(Xm)+EXP(t));
end;
Function Betta_Zero (time:real): real; { Функция Betta[0] для прогонки }
begin
If SelectFunction=1 then Betta_Zero:=(h/(Betta_1*h-Alfa_1))*(Alfa_1*3*SQR(x0)+
Betta_1*(SQR(x0)*x0+SQR(time)));
If SelectFunction=2 then Betta_Zero:=(h/(Betta_1*h-Alfa_1))*(Alfa_1*(2*x0*SQR(time)*time+
10*time+SQR(SQR(time)))+Betta_1*(SQR(x0)*SQR(time)*time+10*x0*time+SQR(SQR(time))*x0));
If SelectFunction=3 then Betta_Zero:=(h/(Betta_1*h-Alfa_1))*(Alfa_1*(SIN(x0*time)+
x0*time*COS(x0*time)-8*x0*COS(time))+Betta_1*(x0*SIN(x0*time)-4*SQR(x0)*COS(time)));
If SelectFunction=4 then Betta_Zero:=(h/(Betta_1*h-Alfa_1))*(Alfa_1*(time*EXP(x0))+
Betta_1*(time*EXP(x0)));
If SelectFunction=5 then Betta_Zero:=(h/(Betta_1*h-Alfa_1))*(Alfa_1*(COS(x0))+
Betta_1*(SIN(x0)+EXP(time)));
end;
Function U_End (time,Alf,Bet:real): real; { Функция Um для прогонки }
begin
If SelectFunction=1 then U_End:=(Alfa_2*h*3*SQR(X)+Betta_2*h*(SQR(X)*X+SQR(time))
+ Bet*Alfa_2)/(Alfa_2-Alf*Alfa_2+h*Betta_2);
If SelectFunction=2 then U_End:=(Alfa_2*h*(2*X*SQR(time)*time+10*time+SQR(SQR(time)))+
Betta_2*h*(SQR(X)*SQR(time)*time+10*X*time+SQR(SQR(time))*X)
+Bet*Alfa_2)/(Alfa_2-Alf*Alfa_2+h*Betta_2);
If SelectFunction=3 then U_End:=(Alfa_2*h*(SIN(X*time)+X*time*COS(X*time)-8*X*COS(time))+
Betta_2*h*(X*SIN(X*time)-4*SQR(X)*COS(time))+Bet*Alfa_2)/(Alfa_2-Alf*Alfa_2+h*Betta_2);
If SelectFunction=4 then U_End:=(Alfa_2*h*(time*EXP(X))+Betta_2*h*(time*EXP(X))+Bet*Alfa_2)/
(Alfa_2-Alf*Alfa_2+h*Betta_2);
If SelectFunction=5 then U_End:=(Alfa_2*h*(COS(X))+Betta_2*h*(SIN(X)+EXP(time))+Bet*Alfa_2)/
(Alfa_2-Alf*Alfa_2+h*Betta_2);
end;
Procedure PrintArray; { Процедура печати массива U }
begin
WriteLn; For m:=0 to Kol_voX do begin Write(U_m[m]:15:4); Write(U,U_m[m]:15:4); end;
WriteLn; WriteLn(U);
end;
{ Основная программа }
Begin
Assign(U,'u'); { Файл для записи значений функции }
Rewrite(U); { Открытие файла для записи }
TextBackGround(0); { Выбор функции для работы }
ClrScr; TextColor(10); GoToXY(20,8); Write('Введите номер выбранной функции (1-5):');
Metka1: ch:=ReadKey;
If ch='1' then SelectFunction:=1
else If ch='2' then SelectFunction:=2
else If ch='3' then SelectFunction:=3
else If ch='4' then SelectFunction:=4
else If ch='5' then SelectFunction:=5
else
begin
Sound(400); Delay(100); NoSound; GoTo Metka1;
end;
GoToXY(59,8);TextColor(12);WriteLn(SelectFunction); TextColor(11); GoToXY(11,12);
Write('Вы будете работать со стандартными параметрами (цифра ~1~)');
GoToXY(22,13); Write('или введете свои данные (цифра ~2~) ?');
Metka2: ch:=ReadKey;
If ch='1' then Data:=1
else If ch='2' then Data:=2
else
begin
Sound(400); Delay(100); NoSound; GoTo Metka2;
end;
TextBackGround(9); TextColor(10); ClrScr;
{ Ввод начальных данных }
WriteLn; WriteLn('-------------------------------- Ввод данных ---------------------------------¬');
For k:=1 do 21 do WriteLn('¦ ¦');
WriteLn('L------------------------------------------------------------------------------');
TextColor(15); Window(3,3,77,23); Write(' Введите область рассчета по X от: ');
If Data=1 then
begin
x0:=0; Write(x0:1:0); WriteLn;
end
else ReadLn(x0);
Write(' до: ');
If Data=1 then
begin
X:=1; Write(X:1:0); WriteLn;
end
else ReadLn(X);
WriteLn; Write(' Введите количество разбиений по направлению X: ');
If Data=1 then begin Kol_voX:=30; Write(Kol_voX:2); WriteLn; end else ReadLn(Kol_voX);
WriteLn;WriteLn; Write(' Введите область рассчета по времени от: ');
If Data=1 then begin t0:=0; Write(t0:1:0); WriteLn; end else ReadLn(t0);
Write(' до: ');
If Data=1 then begin T:=1; Write(T:1:0); WriteLn; end else ReadLn(T);
WriteLn; Write(' Введите количество разбиений по времени: ');
If Data=1 then begin Kol_voT:=30; Write(Kol_voT:2); WriteLn; end else ReadLn(Kol_voT);
WriteLn;WriteLn; WriteLn(' Введите коэффициенты'); Write(' a=');
If Data=1 then begin a:=1; Write(a:1:0); WriteLn; end else ReadLn(a);
Write(' b=');
If Data=1 then begin b:=1; Write(b:1:0); WriteLn; end else ReadLn(b);
Write(' v=');
If Data=1 then begin v:=0.001; Write(v:1:3); WriteLn; end else ReadLn(v);
Write(' Alfa-1=');
If Data=1 then begin Alfa_1:=1; Write(Alfa_1:1:0); WriteLn; end else ReadLn(Alfa_1);
Write(' Betta-1=');
If Data=1 then begin Betta_1:=1; Write(Betta_1:1:0); WriteLn; end else ReadLn(Betta_1);
Write(' Alfa-2=');
If Data=1 then begin Alfa_2:=1; Write(Alfa_2:1:0); WriteLn; end else ReadLn(Alfa_2);
Write(' Betta-2=');
If Data=1 then begin Betta_2:=1; Write(Betta_2:1:0); WriteLn;TextColor(14);
Write(' Нажмите любую клавишу'); ReadKey; end else ReadLn(Betta_2);
{ Интерфейс экрана при выдаче результата }
TextBackGround(3); TextColor(1); Window(1,1,80,25); ClrScr; WriteLn;
WriteLn('г===================== Результат ==========================¬');
For k:=1 to 21 do
WriteLn('¦ ¦');
WriteLn('===================================================================-');
TextColor(0); TextBackGround(7); GoToXY(2,23);
WriteLn(' Для продолжения нажмите любую клавишу'); TextBackGround(3); Window(3,4,77,22);
TextColor(15); ClrScr;
{ Вычесление шага сетки }
tau:=(T-t0)/Kol_voT; h:=(X-x0)/Kol_voX;
{ Ввод данных при time=t0 }
For m:=0 to Kol_voX do
begin
Xm:=x0+h*m; U_m[m]:=Fun_U(Xm,t0);
end;
TextColor(14); WriteLn('Время равно ',time:3:3); TextColor(15); WriteLn(U,'Время равно ',time:3:3);
PrintArray;
{ Начало рассчета }
time:=t0;
Repeat
time:=time+tau;
WriteLn; TextColor(14); WriteLn('Время равно ',time:3:3); TextColor(15);
WriteLn(U,'Время равно ',time:3:3);
{ 1 этап. Решается методом скалярной прогонки }
a_progonka:=(-2*v-a*h)/(2*SQR(h)); b_progonka:=(SQR(h)+2*v*tau-b*tau*SQR(h))/(SQR(h)*tau);
c_progonka:=(a*h-2*v)/(2*SQR(h));
Alfa[0]:=Alfa_1/(Alfa_1-Betta_1*h); Betta[0]:=Betta_Zero(time);
For m:=1 to Kol_voX-1 do
begin
Alfa[m]:=-c_progonka/(a_progonka*Alfa[m-1]+b_progonka);
Betta[m]:=(Fun_F(x0+m*h,time+tau,a,b,v)+U_m[m]/tau-a_progonka*Betta[m-1])/
(a_progonka*Alfa[m-1]+b_progonka);
end;
U_[Kol_voX]:=U_End(time,Alfa[Kol_voX-1],Betta[Kol_voX-1]);
For m:=Kol_voX-1 downto 1 do U_[m]:=Alfa[m]*U_[m+1]+Betta[m];U_[0]:=Alfa[0]*U_[1]+Betta[0];
{ 2 этап, часть первая. Решается методом скалярной прогонки }
a_progonka:=(-2*v-a*h)/(2*SQR(h)); b_progonka:=(2*SQR(h)+2*v*tau-b*tau*SQR(h))/(SQR(h)*tau);
c_progonka:=(a*h-2*v)/(2*SQR(h));
Alfa[0]:=Alfa_1/(Alfa_1-Betta_1*h); Betta[0]:=Betta_Zero(time);
For m:=1 to Kol_voX-1 do
begin
Alfa[m]:=-c_progonka/(a_progonka*Alfa[m-1]+b_progonka);
Betta[m]:=(Fun_F(x0+m*h,time+tau/2,a,b,v)+2*U_m[m]/tau-a_progonka*Betta[m-1])/
(a_progonka*Alfa[m-1]+b_progonka);
end;
_U_1_2[Kol_voX]:=U_End(time,Alfa[Kol_voX-1],Betta[Kol_voX-1]);
For m:=Kol_voX-1 downto 1 do _U_1_2[m]:=Alfa[m]*_U_1_2[m+1]+Betta[m];
_U_1_2[0]:=Alfa[0]*_U_1_2[1]+Betta[0];
{ 2 этап, часть вторая. Решается методом скалярной прогонки }
a_progonka:=(-2*v-a*h)/(2*SQR(h)); b_progonka:=(2*SQR(h)+2*v*tau-b*tau*SQR(h))/(SQR(h)*tau);
c_progonka:=(a*h-2*v)/(2*SQR(h));
Alfa[0]:=Alfa_1/(Alfa_1-Betta_1*h); Betta[0]:=Betta_Zero(time);
For m:=1 to Kol_voX-1 do
begin
Alfa[m]:=-c_progonka/(a_progonka*Alfa[m-1]+b_progonka);
Betta[m]:=(Fun_F(x0+m*h,time+tau,a,b,v)+2*_U_1_2[m]/tau-a_progonka*Betta[m-1])/
(a_progonka*Alfa[m-1]+b_progonka);
end;
_U_1[Kol_voX]:=U_End(time,Alfa[Kol_voX-1],Betta[Kol_voX-1]);
For m:=Kol_voX-1 downto 1 do _U_1[m]:=Alfa[m]*_U_1[m+1]+Betta[m];
_U_1[0]:=Alfa[0]*_U_1[1]+Betta[0];
{ 3 этап. Окончательное значение }
For m:=0 to Kol_voX do
U_m[m]:=2*_U_1[m]-U_[m];
PrintArray; { Вывод результата на экран и его запись в файл }
For m:=0 to Kol_voX do { Рассчет точного значения функции }
begin z[m]:=Fun_U(x0+m*h,time); end;
{ Вывод ошибки расчета на экран и в файл }
Error:=0;
For m:=0 to Kol_voX do
begin
a:=Abs(U_m[m]-z[m]); If Error<a then Error:=a;
end;
WriteLn; TextColor(4); WriteLn('Максимальная ошибка для этого времени равна ',Error:10:7);
TextColor(15); WriteLn(U,'Максимальная ошибка для этого времени равна ',Error:15:13);
WriteLn(U); ReadKey;
Until time>T;
Close(U); { Закрытие файла с результатами }
End.
Похожие работы
... в упругих системах, Докл. АН СССР, 64 (6), 779-782. 4. Вольмир А.С. (1972), Нелинейная динамика пластинок и оболочек, М.: Наука. 5. Березовский А.А., Жерновой Ю.В. (1981), Нелинейные продольно-поперечные стационарные волны в упругих стержнях, В сб.: Мат. Физика, Киев, Наукова думка, 30, 41-48. 6. Болотин В.В. (1956), Динамическая устойчивость упругих систем, М.: Гостехиздат. 7. Беляев
... диаметрах критического сечения представлены на рисунке 2.24 Рисунок 2.24 - Зависимость оптимальной высоты поднятия фурмы от давления при различных диаметрах критического сечения сопла Лаваля 3. Численное исследование движения жидкости Приведены уравнения Навье - Стокса установившегося осесимметричного движения несжимаемой вязкой жидкости в переменных функция тока - вихрь. Проведено ...
... - α) / (2 + α)) yk - 1 + (α/ (2 + α)) (xk + xk - 1). (9) В лабораторной работе производится оценка ошибок цифрового моделирования для каждого из этих методов. Моделирование линейных замкнутых систем Нужно быть очень внимательным при выборе интервала дискретизации, когда моделируются замкнутые системы. В этих системах текущее значение входного процесса сравнивается со ...
... себя почти все методы оценки издержек и экономических выгод, а также относительной рентабельности деятельности предприятия. Типичная «экономическая» модель основана на анализе безубыточности, методе принятия решений с определением точки, в которой общий доход уравнивается с суммарными издержками, т.е. точки, в которой предприятие становится прибыльным. Эти модели широко применяются в бухгалтерском ...
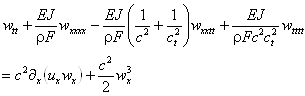
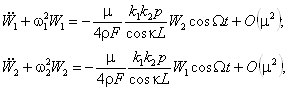
0 комментариев