Оглавление:
Вступление…………………………………………………………………………………..2
Шар и сфера…………………………………………………………………………………3
Шар и шаровая поверхность……………………………………………………...3
Взаимное расположение шара и плоскости……………………………………..3
Принцип Кавальери. Нахождение объёмов тел с помощью принципа Кавальери…………………………………………………………………………..6
Интегральное исчисление. Понятие интеграла…………………………………9
Вычисление объёмов тел с помощью интеграла………………………………10
Объём шара………………………………………………………………………12
Шаровой сегмент. Объём шарового сегмента…………………………………12
Шаровой слой. Объём шарового слоя…………………………………………14
Шаровой сектор. Объём шарового сектора……………………………………14
Площадь поверхности шара…………………………………………………17
Площадь поверхности сектора шара……………………………………….18
Площадь поверхности шарового пояса…………………………………….18
3.Задачи………………………………………………………………………………………20
3.1 Задачи на поверхности…………………………………………………………..20
3.2 Задачи на объёмы тел……………………………………………………………23
4.Заключение…………………………………………………………………………………25
5.Литература………………………………………………………………………………....26
1
2. Шар и сфера.
2.1. Шар и шаровая поверхность.
Ш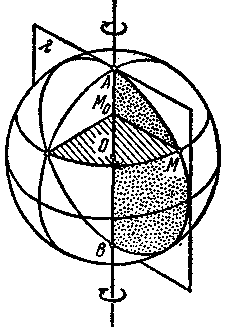
аровой
или
сферической
поверхностью
называется
геометрическое
место точек
пространства,
удаленных от
данной точки
О (центра)
на заданное
расстояние
R
(радиус).
Все пространство
по отношению
к данной шаровой
поверхности
разбивается
на внутреннюю
область (куда
можно присоединить
и точки самой
поверхности)
и внешнюю.
Первая из этих
областей называется
шаром.
Итак,
шар — геометрическое
место всех
точек, удаленных
от
заданной точки
О (центра)
на расстояние,
не превышающее
данной величины
R (радиуса).
Шаровая поверхность
является
границей, отделяющей
шар от окружающего
пространства.
Шаровую поверхность и шар можно получить также, вращая окружность (круг) вокруг одного из диаметров.
Рассмотрим окружность с центром О и радиусом R (рис. 1), лежащую в плоскости Я. Будем вращать ее вокруг диаметра АВ. Тогда каждая из точек окружности, например М, в свою очередь опишет при вращении окружность, имеющую своим центром точку М0—проекцию вращающейся точки М на ось вращения АВ. Плоскость этой окружности перпендикулярна к оси вращения. Радиус ОМ, ведущий из центра исходной окружности в точку М, будет сохранять свою величину во все время вращения, и потому точка М все время будет находиться на сферической поверхности с центром О и радиусом R. Шаровая поверхность может быть получена вращением окружности вокруг любого из ее диаметров.
Сам шар как тело получается вращением круга; ясно, что для получения всего шара достаточно вращать полукруг около ограничивающего его диаметра.
2.2. Взаимное расположение шара и плоскости.
И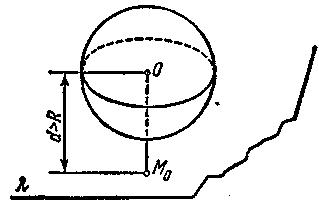
сследуем
вопрос о взаимном
расположении
шара и плоскости.
Для этого, имея
некоторый шар
и плоскость 
,
опустим
из центра
шара перпендикуляр
на плоскость.
Если основание
этого перпендикуляра
М0
окажется
вне шара (рис. 2), то остальные
точки
плоскости и
подавно будут
лежать вне
шара, так как
они еще больше
удалены от
центра, чем
основание
перпендикуляра.
В этом
случае плоскость
не имеет общих
точек с шаром,
она его
не пересекает.
Если основание
перпендикуляра
окажется на
шаровой
поверхности
(рис. 3), то остальные
точки плоскости,
как и в предыдущем
случае, будут
лежать вне
шара. Плоскость
будет
иметь одну
общую точку
с
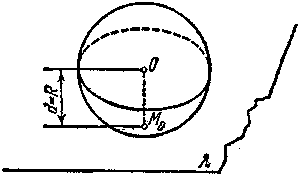поверхностью;
такая плоскость
называется
касательной
к шару.
Радиус, проведенный
в точку
касания, перпендикулярен
к касательной
плоскости.
Д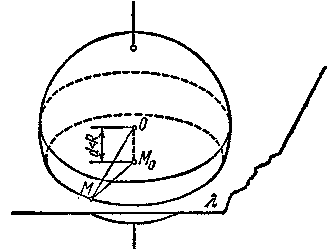
ействительно,
если плоскость
имеет
с поверхностью
шара единственную
общую течку,
то эта точка
ближайшая к
центру шара
по
сравнению с
остальными
точками
плоскости и
потому служит
основанием
перпендикуляра,
опущенного
из центра шара
на плоскость.
Е
сли,
наконец, основание
перпендикуляра
М0
окажется
внутри
шара (рис. 4), то
плоскость будет
пересекать
поверхность
шара,
так как часть
ее окажется
внутри шара,
а часть — вне.
Исследуем
линию пересечения
такой плоскости
с шаровой
поверхностью.
Пусть расстояние
ее от центра
шара равно d,
dR плоскость не пересекает шара;
при d = R плоскость касается шара в одной точке, радиус,
проведенный в точку касания, перпендикулярен к плоскости;
при d
Похожие работы
азывается радиусом сферы. Отрезок, соединяющий две точки сферы и проходящий через её центр, называется диаметром сферы. Шар-это фигура, состоящая из всех точек пространства, находящихся на расстоянии не большем данного от данной точки (или фигура, ограниченная сферой). Уравнение сферы. M(x;y;z)-произвольная точка, принадлежащая сфере. след. MC= т.к. MC=R, то если т.М не лежит на ...
... заданиями, особенно, если карточка с заданием индивидуальна и ученик может работать в ней. Глава II Использование различных форм контроля на уроках математики. Одним из существенных моментов в организации обучения является контроль за знаниями и умениями учащихся. От того, как он организован, на что нацелен существенно зависит содержание работы на уроке, как всего класса в целом, так и ...
... Мухаммед не міг знати. Як би там не було, однак, хадіси Сунни опинилися в руках ісламських богословів цінним матеріалом, який допомагає їм доповнювати та тлумачити Коран і розробляти норми мусульманського права, шаріату. У хадісах також можна зустріти різне правове нашарування, що відображає розвиток соціальних відносин в арабському суспільстві. Остаточне редагування хадісів було здійснене у IX ...
... ї аргентинської пампи був найвологішим, починаючи з 1860 року і приніс небачену відтоді кількість дощових днів, і, як наслідок, жахливі повені, що поглинули близько 2 млн. га сільськогосподарських угідь. Озоновий шар обгортає планету, як щит, що захищає її поверхню від шкідливого сонячного ультрафіолетового проміння. На жаль, він щораз зменшується через різні фактори. Одним з найнебезпечніших є ...
0 комментариев