Навигация
Формирование векторного представления контура
9544
знака
1
таблица
2
изображения
3. Формирование векторного представления контура
После выполнения алгоритма прослеживания контура и выявления контрольных точек имеется три вектора:
, 
,
- абсциссы, ординаты и веса контрольных точек соответственно. Тройку 
назовем скелетом изображения 
. Далее вычислим:
центр масс контрольных точек 
, где 
, 
;
длины радиус-векторов контрольных точек относительно центра масс: 
, 
,
а также длины нормированных радиус-векторов 
, где 
;
косинусы углов между соседними радиус-векторами контрольных точек: 
, ( считая 
, 
)
Из вычисленных компонент составляем векторы 
. Векторы 
будут инвариантны относительно сдвига, поворота и гомотетии изображения относительно центра масс (если «замкнуть» эти векторы, считая 
). Четверку 
будем называть нормированным векторным представлением изображения . Рассмотрим вопрос об устойчивости центра масс изображения к добавлению новой контрольной точки.
Теорема 1. Если к нормированному векторному представлению 
добавить контрольную точку 
с весом 
, то для евклидова расстояния между новым центром тяжести 
и старым 
справедлива оценка 
, где 
- точки скелета изображения . В частности, если 
, то 
.
Другими словами, если число контрольных точек достаточно велико, а вес новой точки небольшой, то центр симметрии сместится незначительно.
4.Функция изображения
Вместо анализа векторного представления в ряде задач (одна из которых будет рассмотрена в следующем разделе) удобней изучать свойства некоторой функции, связывающей векторы из представления . Например, рассмотрим функцию 
,
где 
(
). Эту функцию можно рассматривать как обобщение дескриптора Фурье [5]. По функции 
коэффициенты 
(а, следовательно, и 
) будут определяться однозначно, как коэффициенты частичной суммы ряда Фурье. По дискретным значениям этой функции 
, коэффициенты можно найти из линейной системы 
,, если значения 
, , такие, что определитель матрицы 
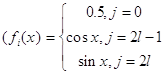отличен от нуля, где 
, где 
- целая часть числа. Множество функций изображения будем рассматривать вместе с нормой 
. Следующая теорема говорит об устойчивости функции изображения к изменению весов (и, следовательно, к изменению центра масс).
Теорема 2. Пусть и 
два скелета изображения такие, что 
. Тогда, если и 
соответствующие этим скелетам функции изображения, то 
, где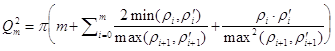 
.
Однако при добавлении новой контрольной точки даже с небольшим весом функция изображения, вообще говоря, может сильно измениться, так как она не является инвариантной относительно сдвига векторов векторного представления . Таким свойством будет обладать, например, функция 
, хотя коэффициенты этой функции уже не будут однозначно восстанавливаться по ее значениям.
5.Распознавание симметрий
Изображение называется 
-осесимметричным [6], если оно переводится само в себя после поворота на любой угол, кратный 
вокруг своего центра масс. Симметрия является важной в задачах распознавания характеристикой изображаемого объекта. Подробный обзор существующих методов обнаружения симметрий и определения ориентации объекта, в том числе и с помощью дескрипторов Фурье, можно найти в работе [6]. Распознавать симметрию можно непосредственно анализируя векторное представления , если оно достаточно точно отражает характер симметрии (не содержит «лишних» контрольных точек). Векторное представление назовем -осесимметричным, если построенный по этому векторному представлению многоугольник будет -осесимметричным. С другой стороны, для распознавания симметрии можно использовать и функцию изображения . В этом случае лучше перейти к комплексной форме записи функции изображения. Обозначим через 
, где 
. Тогда 
и справедлива
Теорема 3. является -осесимметричным векторным представлением изображения тогда и только тогда, когда найдется такое 
, что 
, 
где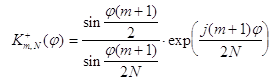
.
Это мультипликативное свойство функции изображения можно использовать для распознавания симметрий, а именно, если для заданного малого 
найдутся такие 
и 
, что 
, то можно считать векторное представление -осесимметричным.
Список литературы
Hecker Y.C., Bolle R.M. On geometric hashing and the generalized Hough transform, IEEE Trans. Syst., Man and Cybern. 24, N9, 1994, p.1328-1338.
Dufresne T.E., Dhawan A.P., Chord-tangent transformation for object recognition, Pattern Recogn. 28, N9, 1995, p.1321-1332.
Bolles R., Cain R.A., Recognizing and locating partiavisible objects: The local-feature-focus method, Robot Vision A.Publ. Ed., 1984.
Liu H.C., Srinath M.D., Partial Shape Classification Using Contour Matching in Distance Transformer; IEEE Trans. Pattern Anal. and Mach. Intell, 12, N11, p.1072-1079.
Zahn C.T., Roskies R.S., Fourier descriptors for plane closed curves, IEEE Trans. Comput. C-21, March, 1972, p.269-281.
Pei S.C., Liov L.G., Automatic symmetry determination and normalization for rotationally symmetric 2D shapes and 3D solid objects, Pattern Recogn, 27, N9, 1994, p.1193-1208. последовательностей".- Таганрог, изд. ТРТУ, 1996 г.
Похожие работы
... для графа на рис. 3, приняв, что дерево образовано ветвями 2, 1 и 5 Ответ: B= Решить задачу 5, используя соотношения (8) и (9). Теория / ТОЭ / Лекция N 3. Представление синусоидальных величин с помощью векторов и комплексных чисел. Переменный ток долгое время не находил практического ...
... . Для одного пользователя, используется для ведения настольной БД или как клиент для подключения к серверу БД. Оценка современных СУБД на соответствие требованиям, предъявляемым к автоматизированным информационным системам кадастра. Рассмотрим стандартные современные реляционные СУБД по каждому классу продуктов, основные возможности, которые они предоставляют. Произведем оценку их, в соответствии ...
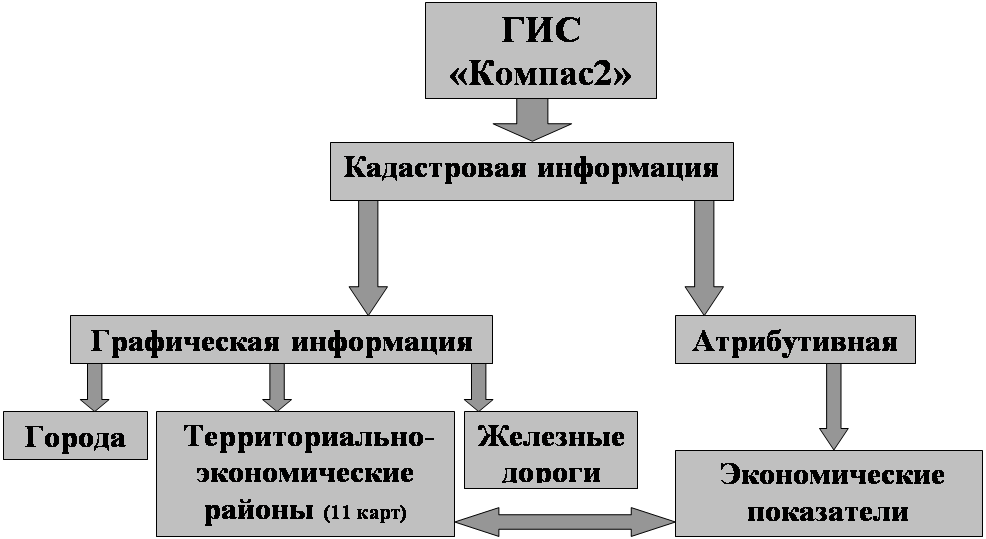
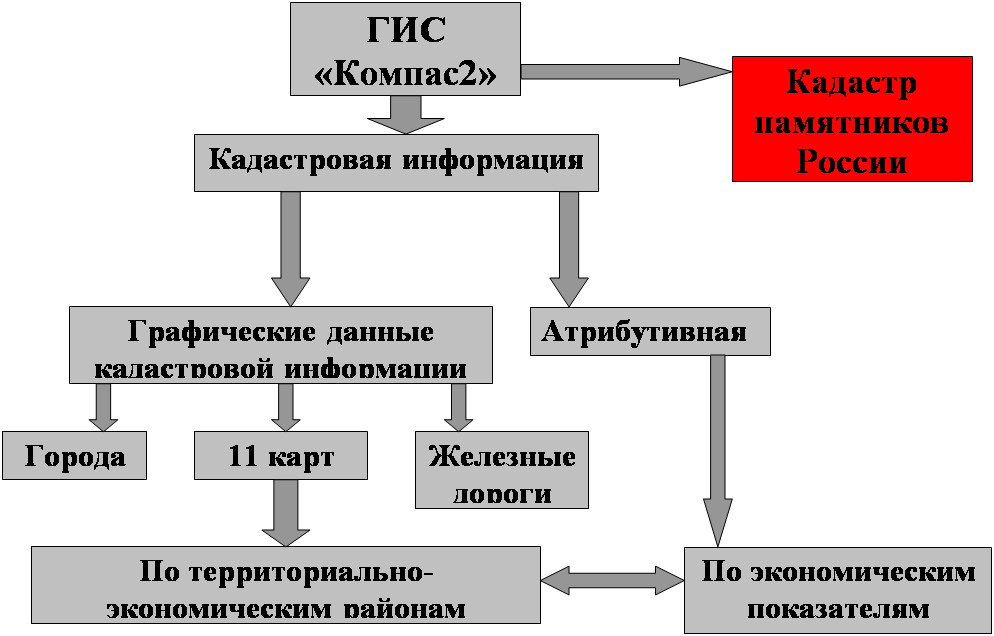
... кадастра памятников России и привязки его к ГИС «Компас-2», я изучил возможности, функции ГИС «Компас-2», а также возможность использования его для создания различных видов природных кадастров. Компас-2 – это сетевая система для представления, моделирования и анализа географической информации Функциональные возможности системы КОМПАС 2: публикация географической информации (ГИ) в сетях ...
... стриммера емкости 1.5 Гбайт, и на лазерный диск при помощи соответствующего устройства. В целом, программное и техническое обеспечение Яррайкомзема является достаточным для автоматизированной обработки землеустроительной информации и позволяет решать большинство возникающих в процессе деятельности задач оперативно, с высокой долей качества и профессионализма. Глава 2. Обработка результатов ...
0 комментариев