Навигация
Простые проценты. Если процентные ставки изменяются во времени
1. Простые проценты. Если процентные ставки изменяются во времени,
| |
| | |
| ||||||
Пример: сделан депозитный вклад по ставке 120% годовых. Счет открыт по германской схеме (К=360). 10 мая положили 20000 д.е., 9 июля сняли 10000 д.е., 8 октября положили 5000 д.е., 27 декабря счет закрыт. Чему равен накопленный процент?
|
2. Сложные проценты.
| |
Пример: на счет положили 1000 д.е. по сложной ставке (ic=100%). Через год добавили 2000 д.е. Еще через год – счет закрыли. Какова ПрS - ?
|
Пример: предлагается сдать участок в аренду на 3 года, выбрав один из вариантов оплаты:
1) 10000 д.е. в конце каждого года:
2) 35000 д.е. в конце трехлетнего срока:
Банковская ставка по депозитному вкладу 20% годовых (ic=20%).
Номинальная и эффективная процентная ставка.
Если проценты начисляются один раз в год, то величина (1+i) показывает, во сколько раз возросла начальная сумма за один год. Годовая процентная ставка i называется эффективной. Однако проценты могут начисляться несколько раз в году. В этом случае указывают номинальную годовую процентную ставку (j), и дополнительно указывают, сколько раз в году происходит начисление процентов (m – число начислений процентов в году).
| |
- наращенная сумма в конце года.
При начислении сложного процента в течении n лет получим
| |
Пример: вклад 2000 д.е. осуществлен на 2 года. Номинальная ставка процента jc=100%. Какова будет накопленная сумма?
Так как дана номинальная ставка, то необходимо указать число ежегодных начислений:
m=1 ®
m=2 ®
m=4 ®
m=12 ®
При непрерывном начислении процентов (ежедневном) (используется на рынке производных ценных бумаг (фьючерсные и опционные контракты)):
Эквивалентность процентных ставок.
При финансовых вычислениях можно пользоваться любыми ставками: простыми, сложными, непрерывными. При этом результаты расчетов не должны зависеть от выбора ставки.
Эквивалентные процентные ставки – ставки разного вида, применение которых при одинаковых начальных условиях дает одинаковые финансовые результаты.
Процедура нахождения эквивалентных ставок:
1) Выбирается величина, которую легко рассчитать при использовании различных процентных ставок, обычно FV;
2) Приравниваются 2 выражения, то есть составляют уравнение эквивалентности;
3) Преобразуя, выражают одну процентную ставку через другую.
| |
iкв=3%;
iгод-?
а) простые ставки процента, уравнение эквивалентности:
б) сложные ставки процента, уравнение эквивалентности:
Пример: что лучше – положить деньги в банк А, начисляющий 24% годовых или в банк Б, начисляющий 10% годовых каждые полгода по схеме сложного процента.
Эквивалентность простой и сложной ставок.
| |
По простой
По сложнойУравнения эквивалентности FVпр = FVсл
Современная стоимость денег. Дисконтирование.
Дисконтирование – обратная операция наращению.
Процесс приведения будущей суммы денег к современной стоимости называется дисконтированием.
Из (1)
| |
| ||||
Пример: будущие доходы распределяются следующим образом
1500 через год;
2000 через 2 года;
3000 через 5 лет.
Чтобы сравнить ценность этих поступлений проведем операцию дисконтирования, то есть приведения к сегодняшнему дню будущей стоимости, при i=20%.
Таким образом, наибольшее предпочтение имеет 2 поток.
Пример: должник должен выплатить 40000 руб. с отсрочкой через 5 лет. Он готов сегодня погасить свой долг из расчета 25% годовых.
Пример: бескупонная облигация будет погашена через 6 лет по номиналу (1000 руб., 100%). По какой цене есть смысл ее приобрести, если депозитная ставка банка на тот же срок 23% (альтернативная доходность).
То есть 28,8% от номинала. Если рыночная цена ниже, чем приведенная стоимость – то покупать разумно, в противном случае покупать не стоит.
Банковское дисконтирование.
Покупка банком любого несобственного векселя до срока его погашения носит название учет векселя. Учет векселя эквивалентен выдаче кредита векселедержателю, за эту операцию банк взимает дисконт (учетный процент).
| |
| ||||
Три задачи, вытекающие из операции учета:
1) Определение рыночной стоимости векселя;
| |
2) Определение срока ссуды
| |
3) Определение размера учетной ставки
Пример: вексель (Н=8000 руб.) учтен банком по d=18,5% годовых за 132 дня до погашения. Какую сумму получил векселедержатель? Какую сумму заработал банк при погашении векселя (Dis)?
Пример: вексель учтен за 60 дней до погашения по простой учетной ставке 20% годовых. При учете получена сумма 7100000 руб. Найти номинал?
Конверсия платежей. Эквивалентность платежей.
Три практические задачи:
1. Определение процентной ставки (простой или сложной).
2. Определение консолидированного платежа.
3. Определение срока консолидированного платежа.
Две суммы S1 и S2, выплачиваемые в разные моменты времени, считаются эквивалентными, если их современные стоимости (PV) или же наращенные стоимости (FV), рассчитанные по одной и той же процентной ставке (i) и на один и тот же момент времени, одинаковы.
А) Дисконтирование. Условие эквивалентности: PV1=PV2, i=const
Б) Наращение. Условие эквивалентности: FV1=FV2
Определение процентной ставки, при которой платежи эквивалентны.
А) Простая ставка процента.
Условие эквивалентности: , тогда
| |
Пример: имеются 2 обязательства:
1) Заплатить S1=4,5 млн. руб. через 3 месяца;
2) S2=5 млн. руб. через 8 месяцев.
Определить ставку процента, при которой платежи S1 и S2 эквивалентны (К=360,12 месяцев)?
Б) Сложная ставка процента.
| |
Сумма консолидированного платежа.
Постановка задачи: пусть Sj – платежи в моменты времени tj (j=1, 2, …., m). So – платеж в момент времени to.
Требуется рассчитать эквивалентную денежную сумму So.
Решение: для одних платежей надо рассчитать их будущую стоимость, то есть произвести операцию наращения; для других платежей обратную операцию – дисконтирование.
Сумма консолидированного платежа определяется по формуле, объединяющей обе операции:
| | |||
| |||
Если ставка процента сложная, то консолидированный платеж определяется по формуле:
| |
Пример: имеется 3 платежа – 5, 3 и 8 млн. руб. со сроками 130, 165 и 320 дней соответственно. Определить консолидированный платеж со сроком 250 дней (простая ставка 20% годовых)(К=365).
Найдем величину ссуды ().
Какова сумма консолидированного платежа на 320 день?
Пример: три платежа 2,4 и 3 млн. руб. со сроками 2, 3 и 4 года соответственно заменяются двумя платежами: через год выплачивается 2 млн. руб., а остаток (х) погашается через 5 лет. Пересчет выполнить по ставке сложного процента 25%. Определить остаток долга через 5 лет.
1) Приведем все платежи к 5 году и составим уравнение эквивалентности, используя операцию наращивания:
2) Найдем остаток, используя дисконтирование:
Для решения этого уравнения умножим все слагаемые на 1,255.
Пример: ссуда выплачивается в следующем порядке:
01.01.02 – 2 млн. руб.
01.07 – 3 млн. руб.
01.01.03 – 4 млн. руб.
01.07 – 5 млн. руб.
Проценты 20% начисляются по сложной ставке.
1) Определить суммарную задолженность на 01.01.04.
2) Определить современную стоимость.
Срок консолидированного платежа.
Из условия эквивалентности платежей , i – простая ставка
| |
Потоки платежей.
Под потоком платежей понимается некоторая последовательность платежей во времени (Cash Flow).
Потоки могут быть:
- Регулярные;
- Нерегулярные.
Элементами нерегулярного потока являются как положительные поступления, так и отрицательные выплаты, а соответствующие платежи могут производиться через различные интервалы времени.
Финансовая рента (аннуитет) – поток одинаковых платежей, все элементы которых положительные величины, а временные интервалы между платежами - одинаковы.
Характеристики ренты:
- Размер платежа (Payment – PMT);
- Период ренты;
- Срок ренты;
- Процентная ставка.
По моменту выплаты в пределах периода между платежами ренты делятся:
a) Постнумерандо – выплаты в конце периода;
b) Пренумерандо – выплаты в начале периода;
c) В середине периода.
Будущая стоимость годовой ренты (FVAn).
Годовая рента постнумерандо предусматривает выплаты и начисления процентов 1 раз в год в конце года.
Постановка задачи: определить наращенную сумму ренты, если в течение n лет в банк в конце каждого года вносится платеж R, на который начисляются сложные проценты по ставке – ic годовая.
Поскольку каждое слагаемое данного ряда имеет постоянный множитель (1+i=n), то эти величины образуют геометрическую прогрессию. Сумма членов этого ряда имеет вид
|
| |
Пример: в фонд ежегодно в течении 7 лет в конце года поступает по 10000 руб., на которые начисляются проценты по ставке 15% годовых. Определить коэффициент наращения? Величину фонда накоплений на конец срока?
Современная стоимость годовой ренты (PVAn).
При расчете современной стоимости ренты используется операция дисконтирования потоков платежей и процентов по ним. Это приводит к появлению геометрической прогрессии, сумма членов которой дает расчетную формулу для современной стоимости аннуитета в 1 руб.
| |
Пример: по исходным данным предыдущей задачи рассчитать современную стоимость конечной величины фонда.
Пример: ежегодный купонный доход в 120 руб., приносимый облигацией с фиксированным доходом, реинвестируется путем помещения на банковский счет под 14% годовых в течении 6 лет. Какая сумма накопится на счете?
Пример: оборудование стоимостью 5 млн. долларов поставляется на следующих условиях:
1) 50% выплачиваются сразу, остальное в рассрочку равными платежами в течении 3 лет, выплаты раз в квартал. Чему должен быть равен платеж, если квартальный ic=6%?
2) Какая сумма образуется на счете фирмы экспортера оборудования по завершении контракта, если она будет вкладывать платежи в банк под ic=2% в квартал?
Управление инвестиционными проектами.
Инвестиционный проект – это особая организационно-обособленная часть инвестиционного процесса.
Три фазы инвестиционного проекта:
I. Прединвестиционная;
II. Собственно инвестиционная;
III. Эксплуатационная.
Денежные потоки инвестиционного проекта.
Эффективность инвестиционного проекта оценивается в течении расчетного периода от начала затрат до ликвидации проекта. Расчетный период разбивается на отрезки, в рамках которых проводится агрегирование данных для оценки финансовой эффективности.
На каждом шаге анализа инвестиционного проекта значение денежного потока характеризуется:1) Притоком (или поступлениями);
2) Оттоком (или платежами);
3) Сальдо.
Денежные потоки возникают по отдельным видам деятельности:
1. Инвестиционная;
2. Операционная;
3. Финансовая.
| Оттоки | Притоки |
| Инвестиционная деятельность | |
| 1) Капитальные вложения; 2) Затраты на пусконаладочные работы; 3) Ликвидационные расходы в конце проекта; 4) Затраты на увеличение оборотного капитала. | 1) Продажа активов в течении и по окончании проекта; 2) Поступления за счет снижения оборотного капитала. |
| Операционная деятельность | |
| Налоги. | 1) Выручка от продаж; 2) Внереализационные доходы, в том числе поступления от вложений в дополнительные фонды, приносящие доход. |
| Финансовая деятельность | |
| 1) Возврат и обслуживание займов, а так же погашение ценных бумаг; 2) Выплата дивидендов акционерам. | 1) Вложения собственного капитала в ценные бумаги других предприятий; 2) Вложение привлеченных средств. |
Кроме притоков и оттоков необходимо выделять доходы и затраты, то есть показатели фактические или планируемые, но не обязательно связанные с движением денежных средств.
Пример: План денежного потока проекта.
| Наименование показателей | Годы | ||
| I | II | III | |
| Производственная деятельность: 1. Выручка от реализации; 2. Прямые затраты; 3. Административные и торгово-сбытовые затраты; 4. Проценты за кредит; 5. Налог на прибыль. | - - -50 - - | 500 -100 -100 -50 -80 | 1000 -200 -200 -50 -250 |
| Сальдо CF от производственной деятельности | -50 | 170 | 300 |
| Инвестиционная деятельность: 1. Инвестиционные затраты (покупка оборудования, патентов, лицензий); 2. Реализация основных средств. | -1000 - | -200 - | - 200 |
| Сальдо CF от инвестиционной деятельности | -1000 | -200 | 200 |
| Финансовая деятельность: 1. Собственный капитал; 2. Заемный капитал; 3. Возврат кредитов; 4. Выплаты дивидендов. | 1000 500 - - | - 200 -100 - | 500 - -100 -100 |
| Сальдо CF от финансовой деятельности | 1500 | 100 | 300 |
| Сальдо CF на начало периода Сальдо CF на конец периода | 0 450 | 450 520 | 520 1320 |
Показатели эффективности инвестиционного проекта.
1. Чистый приведенный доход NPV, NPV>0;
2. Индекс рентабельности PI>1;
3. Срок окупаемости PP (чем меньше, тем лучше);
4. Внутренняя норма рентабельности IRR.
Чистая приведенная стоимость.
Чистая приведенная стоимость рассчитывается алгебраическим сложением дисконтированных инвестиций и дисконтированных доходов.
Схема инвестиционного проекта.
Индекс рентабельности:
В частном случае:
Если
Срок окупаемости.
PP – это период времени, в течении которого сумма полученных доходов окажется равной величине произведенных инвестиций.
Два метода:
I. Не использующий концепцию дисконтирования. Применяется для краткосрочных инвестиционных проектов, когда влияние фактора времени не учитывается, когда уровень дохода примерно стабилен по периодам.
II. Основанный на дисконтировании притоков и оттоков проекта. При этом производится прямое сопоставление общей величины инвестиций с суммой доходов, определенных нарастающим итогом.
При определении точной величины срока окупаемости, включающее целое число лет и некоторую дробную часть года, необходимо:
1) Определить целое число лет, в течении которых происходит полная окупаемость инвестиций (m);
2) Определить период, меньший срока окупаемости на 1 год (m-1);
3) Определить часть инвестиций, которая окупится за последний год срока окупаемости (DI).
Величина дисконтирования инвестиций DI окупится за некоторую часть периода Dm.
Внутренняя норма рентабельности проекта.
IRR – это ставка дисконта, при которой чистая приведенная стоимость равна нулю (NPV=0).
Методы нахождения IRR:
1) Аналитический;
2) Графический;
3) Метод подбора с использованием формулы линейной интерполяции.
Чем выше IRR, тем более эффективен инвестиционный проект. Лучше всего, если IRR больше или, в крайнем случае, равен:
1) Среднеотраслевой доходности;
2) Средней ставке кредита, привлекаемого для капитальных вложений;
3) Средней цене капитала WACC<IRR;
4) Больше чем сложный процент банковской ставки.
Пример: определить показатели инвестиционного проекта, если денежный поток проекта имеет вид
Оценку показателей выполним при ставке дисконтирования r=10%.
| Год, t | 1 | 2 | 3 | 4 | 5 | 6 |
| CF | -200 | -100 | 50 | 200 | 400 | 500 |
Допустим, что методом подбора получено, что r1=0.4, заменяем х=0,4 и рассчитываем NPV1= 17,18. При r2=0.5, x=0.5, NPV2=-26,89. Воспользуемся формулой линейной интерполяции и рассчитаем IRR.
| N | 1 | 2 | 3 | 4 |
| 1 | -100 | 90 | 45 | 9 |
| 2 | -100 | 10 | 50 | 100 |
Пример: определить ставку дисконтирования, при которой оба проекта равноценны.
Умножим все слагаемые на (1+r)4, перенесем все слагаемые, раскроем скобки, задача упростится, если принять (1+r)=х
Экономическая рентабельность. Формула Дюпона.
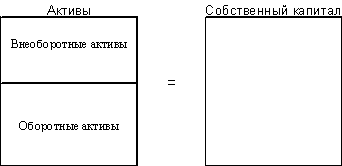
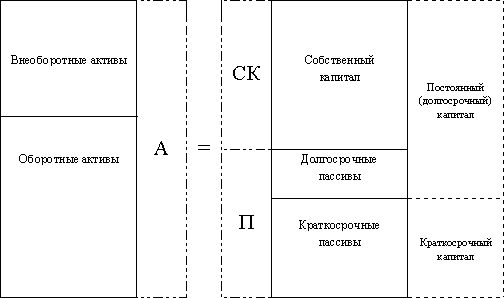
Экономический эффект, снимаемый предприятием с производимых затрат, представляет собой прибыль до уплаты процентов за кредиты и займы и налога на прибыль. Это называется нетто-результат эксплуатации инвестиций (НРЭИ).
| |
| |
, так как А=П, П=СК+ЗК
СК – собственный капитал;
ЗК – заемный капитал;
ВР – выручка.
Коммерческая маржа (КМ) в процентах показывает, какой результат эксплуатации дают каждые 100 руб. выручки.
Коэффициент трансформации (КТ) показывает, сколько раз за данный период оборачивается каждый рубль активов.
Двухфакторная формула Дюпона.
| |
Формула Дюпона – факторная модель анализа коэффициентов рентабельности. Назначение модели – идентифицировать факторы, определяющие эффективность функционирования предприятия, оценить степень их влияния и тенденции в изменении их значимости.
На коммерческую маржу влияют следующие факторы:
1. Объем реализации;
2. Ценовая политика;
3. Структура затрат.
На коэффициент трансформации оказывают действие:
1. Отраслевые условия деятельности предприятия;
2. Экономическая стратегия предприятия.
Примерить высокую коммерческую маржу с высоким коэффициентом трансформации очень трудно, поскольку выручка присутствует в числителе одного коэффициента и в знаменателе другого.
Трехфакторная модель Дюпона.
Она рассматривает рентабельность собственного капитала (РСК) или чистую рентабельность акционерного капитала.
| |
Привлечение заемных средств увеличивает рентабельность собственного капитала.
При возрастании рентабельности акционерного капитала по этой формуле можно определить за счет чего это произошло:
1. Благодаря увеличению чистой прибыли (ЧП) на каждый рубль оборота;
2. За счет более эффективного использования активов;
3. За счет изменения акционерного капитала (рационального использования);
4. За счет сопряженного воздействия факторов.
Четырехфакторная модель Дюпона.
Кg – коэффициент устойчивости экономического роста.
| |
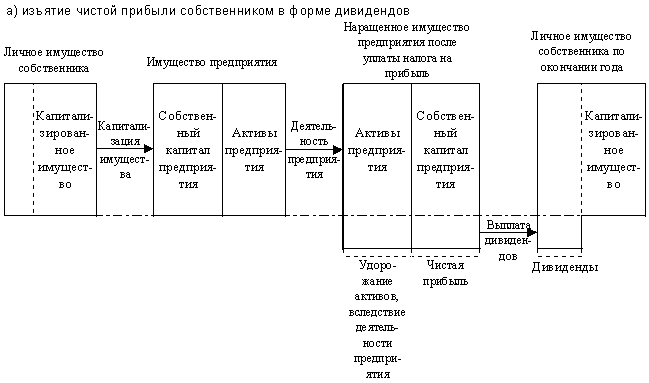
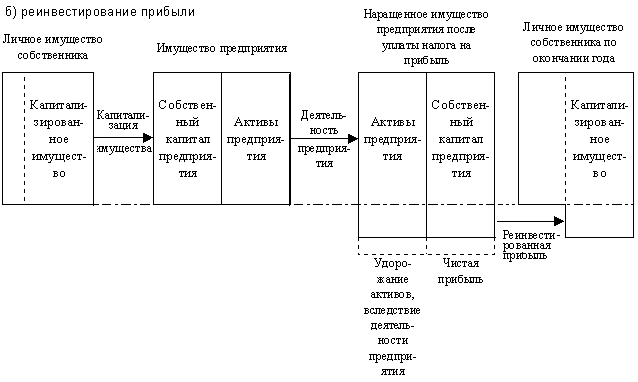
Распределение прибыли. Дивидендная политика.
Акции
Источники выплаты дивидендов:
1. Чистая прибыль отчетного периода;
2. Нераспределенная прибыль прошлых периодов;
3. Специальный фонд, используемый для выплаты дивидендов по привилегированным акциям при недостаточности прибыли.
Дивидендная политика – решения, которые принимает компания в зависимости от типа, размера и периодичности выплат держателям обыкновенных акций.
Оптимальная дивидендная политика – стратегия, которая помогает максимизировать рыночную стоимость фирмы. Под рыночной стоимостью фирмы (РСТФ) понимается совокупная стоимость ее собственных и заемных средств.
Факторы, влияющие на дивидендную политику:
1. Ограничения правового характера;
2. Ограничения контрактного характера, то есть запрет на выплату дивидендов при использовании заемного капитала;
3. Ограничения финансового характера. Выплата дивидендов снижает ликвидность компании;
4. Ограничение в связи с расширением производства.
Виды дивидендной политики предприятия.
1. Политика фиксированных дивидендных выплат. Предусматривает регулярность выплат в течении продолжительного срока независимо от изменения курсовой стоимости акции . Недостаток: если прибыль сильно снижается, выплата фиксированного дивиденда снижает ликвидность компании.
2. Политика постоянного процента дивидендных выплат (процент от прибыли). Недостаток: в неблагоприятные годы дивиденды могут существенно упасть, эта политика не ведет к росту курсовой стоимости, так как большинство акционеров отрицательно относятся к изменению суммы выплачиваемых дивидендов.
3. Политика компромиссного подхода к дивидендным выплатам. То есть компания выплачивает какой-то дивиденд, а в благоприятные годы надбавку (экстра-дивиденд). Недостаток: надбавки не должны выплачиваться регулярно, так как это противоречит политике.
Похожие работы
... (2.2.44) Сложная номинальная процентная ставка (j) (2.2.45) (2.2.46) Сложная учетная ставка (dсл) (2.2.47) (2.2.48) – По мере усложнения задач, стоящих перед финансовым менеджментом, сфера применения непрерывных процентов будет расширяться, так как при этом становится возможным использовать ...
... 37,308 R19992= 2,227 R1997= 9,159 R1998= 6,108 R1999= 1,492 ГЛАВА 4. РЕКОМЕНДАЦИИ ПО СОВЕРШЕНСТВОВАНИЮ ФИНАНСОВОГО МЕНЕДЖМЕНТА ОРГАНИЗАЦИИ 4.1. Направления совершенствования финансового менеджмента Управление финансами стало важнейшей сферой деятельности любого субъекта социально-рыночного хозяйства, ...
... организации высокоэффективного управления его финансами. Такое управление финансами отдельных субъектов хозяйствования выделилось в странах с рыночной экономикой в начале XX века в специальную область знаний, которая получила название “финансовый менеджмент”. Он представляет собой процесс управления формированием, распределением и использованием финансовых ресурсов хозяйствующего субъекта и ...
... предприятия; · самофинансирования, · материальной заинтересованности, · материальной ответственности, · обеспеченности рисков финансовыми резервами. II. Базовые концепции финансового менеджмента 2.1 Концепция временной стоимости денег Концепция изменения стоимости денег во времени играет центральную роль в практике финансовых вычислений и ...







0 комментариев