Навигация
Методика изучения дробных чисел
2.3 Методика изучения дробных чисел
В практике преподавания основным методом изучения дробных чисел являются поясняющие описания, которые опираются на жизненный опыт и знания учащихся. Поясняющие описания не заменяют определений, понятий, а лишь показывают целесообразность их введения.
Введение дробных чисел в школьном курсе связывается с необходимостью более точного измерения величин, с делением чисел. В связи с этим целесообразно познакомить учащихся с возникновением дробных чисел в процессе практической деятельности человека, а именно в процессе измерения. Краткая историческая справка поможет учащимся лучше овладеть данным материалом. Содержание её может быть примерно следующим.
Измерение, так же как и счет, имело место у всех народов с самых древних времён; измерение было непосредственно связано со счетом. Потребность в более точном измерении явилась причиной того, что единицы мер стали раздроблять на две, на три и более частей. Этим более мелким мерам давали особые наименования, и в дальнейшем величины измерялись уже этими более мелкими единицами, однородными с ними. Так возникли первые конкретные дроби. Отвлеченных дробей в это время еще не знали.
Длинен был путь перенесения названия какой-либо части одной меры на такую же часть другой меры, это был путь создания абстрактного понятия дроби.
Так, например, в России была земельная мера четверть и более мелкая – получетверть, которая называлась осьмина. Это были конкретные дроби, единицы для измерения площади земли, но осьминой нельзя было измерить время или скорость и др. Значительно позднее осьмина стала означать отвлеченную дробь 1/8, которой можно выразить любую величину. Дроби первоначально в русских рукописях назывались долями, затем ломаными числами. При записи числа использовалась горизонтальная черта.
Довольно долгим был путь и к введению десятичных дробей. В древности некоторые народы пользовались шестидесятеричной системой счисления и дроби записывались в шестидесятеричной системе так же, как в настоящее время записывают наши десятичные дроби. Римляне пользовались двенадцатеричными дробями.
В 16 – 17 вв. в связи с развитием общества, с развитием науки и техники возникла необходимость облегчить громоздкие вычисления. Внимание математиков было обращено к десятичным дробям, к десятичной системе мер. В России учение о десятичных дробях впервые было изложено в «Арифметике» Магницкого, где были приведены и десятичные меры длины и площади. В этой же работе излагается и учение о шестидесятеричных дробях (отголосок вавилонской шестидесятеричной системы счисления).
Учащимся нужно также показать, что дроби применяются не только в математике, но и, например, в музыке.
Все знают, что Пифагор был учёным и, в частности, автором знаменитой теоремы. А то, что он был еще и блестящим музыкантом, известно не так широко. Сочетание этих дарований позволило ему первым догадаться о существовании природного звукоряда. Надо было ещё доказать это. Пифагор построил для своих экспериментов полуинструмент-полуприбор — «монохорд». Это был продолговатый ящик с натянутой поверх него струной. Под струной, на верхней крышке ящика, Пифагор расчертил шкалу, чтобы удобнее было зрительно делить струну на части. Множество опытов проделал Пифагор с монохордом и, в конце концов, описал математически поведение звучащей струны. Работы Пифагора легли в основу науки, которую мы называем сейчас музыкальной акустикой.
Оказывается, для музыки семь звуков внутри октавы такая же естественная вещь, как десять пальцев на руках в арифметике. Уже тетива самого первого лука, колеблясь после выстрела, давала готовым тот набор музыкальных звуков, которыми мы почти без изменения пользуемся до сих пор.
С точки зрения физики тетива и струна — одно и то же. Да и сделал человек струну, обратив внимание на свойства тетивы. Звучащая струна колеблется не только целиком, но одновременно и половинками, третями, четвертями и т.д. Подойдём теперь к этому явлению с арифметической стороны. Половинки колеблются вдвое чаще, чем целая струна, трети — втрое, четверти — вчетверо. Словом, во сколько раз меньше колеблющаяся часть струны, во столько же раз больше частота её колебаний. Допустим, вся струна колеблется с частотой 24 герца. Высчитывая колебания долей вплоть до шестнадцатых, мы получим ряд чисел, показанных в таблице. Эта последовательность частот так и называется — натуральный, т.е. природный, звукоряд.
| 1 | |||||||||||||||
| 24 | 48 | 72 | 96 | 120 | 144 | 168 | 192 | 216 | 240 | 264 | 288 | 321 | 336 | 360 | 384 |
Согласно программе и учебнику по математике формирование понятий дроби начинается с умения получать доли при делении какой-либо величины на несколько равных частей.
Учащимся предлагается разделить на равные части знакомые предметы, такие, как арбуз, дыня, пирог и др., и выделить одну из частей, одну из долей. Такие же по характеру упражнения выполняют учащиеся с использованием геометрического материала: деление отрезка, круга, квадрата на равные части, на равные доли и взятие одной такой части, одной доли. От выделения одной части и взятию нескольких таких частей.
Учащимся сообщается, что для выражения одной или нескольких долей предмета нужны новые числа, а именно дроби. Далее приводятся примеры обыкновенных дробей и даётся форма записи обыкновенной дроби, проводится обучение чтению. Учащиеся должны помнить: числитель дроби — количественное числительное женского рода (одна, две и т.д.), а знаменатель — порядковое числительное (седьмая, сотая, двести тридцатая и т.д.).
Например, — одна пятая; — две шестых; — семь десятых;
— восемьдесят три сто пятьдесят вторых. В процессе работы над закреплением понятия дроби необходимо познакомить учащихся с происхождением слова «дробь», ввести термины «числитель», «знаменатель». Это можно сделать следующим образом.
В начале урока учащимся можно предложить три ребуса:
|
|
|
После их разгадывания можно сообщить им следующие исторические сведения.
С древних времён людям приходилось не только считать предметы, но и измерять длину, время, площадь, вести расчеты за купленные или проданные товары.
Не всегда результат измерения или стоимость товара удавалось выразить натуральным числом. Приходилось учитывать и части, доли меры. Так появились дроби.
В русском языке слово дробь появилось в VIII веке, оно происходит от глагола «дробить» — разбивать, ломать на части. В первых учебниках математики (в VII веке) дроби так и назывались — «ломаные числа». У других народов название дроби также связано с глаголами «ломать», «разбивать», «раздроблять».
Современное обозначение дробей берет свое начало в Дровней Индии; его стали использовать и арабы, а от них в XII-XIV веках оно было заимствовано европейцами. Вначале в записи дробей не использовалась дробная черта; например, числа , записывались так: , . Черта дроби стала постоянно использоваться лишь около трехсот лет назад. Первым европейским ученым, который стал использовать и распространять современную запись дробей, был итальянский купец и путешественник, сын городского писаря Фибоначчи (Леонардо Пизанский). В 1202 г. он ввел слово «дробь». Названия «числитель» и «знаменатель» ввел в XIII веке Максим Плануд — греческий монах, ученый-математик.
Десятичные дроби вводятся в связи с рассмотрением позиционной системы. Десятичная дробь появляется как частный случай обыкновенной дроби, как способ записи дробей со знаменателем 10ⁿ (1/10, 3/1000 и др.), второе условие относится к форме записи (0,1; 0,003 и др.).
Мотивацию их введения можно связать с тем, что в науке и промышленности, в сельском хозяйстве при расчетах десятичные дроби используются гораздо чаще, чем обыкновенные.
Это связано с простотой правил вычислений с десятичными дробями, похожестью их на правила действий с натуральными числами. Правила вычислений с десятичными дробями описал знаменитый ученый средневековья Аль-Каши Джемшид ибн Масуд, работавший в городе Самарканде в обсерватории Улугбека в начале XV века.
Записывал Аль-Каши десятичные дроби так же, как принято сейчас, но он не пользовался запятой: дробную часть он записывал красными чернилами или отделял вертикальной чертой.
Но об этом в Европе в то время не узнали, и только через 150 лет десятичные дроби были заново изобретены фламандским инженером и ученым Симоном Стевином. Стевин записывал десятичные дроби довольно сложно.
Например, число 24,56 выглядело так 2456 или — вместо запятой нуль в кружке (или 0 над целой частью), цифрами 1, 2, 3,…, помечалось положение остальных знаков.
Запятая или точка для отделения целой части стали использоваться с XVII века.
В России учение о десятичных дробях изложил Леонтий Филиппович Магницкий в 1703 году в первом учебнике математики «Арифметика, сиречь наука числительная».
При изучении действий с дробями огромный гуманитарный потенциал кроется в содержании упражнений, которые можно использовать на уроках:
- связанные с литературой:
Задача 1. Три неразлучных друга Винни-Пух, Кролик и Пятачок решили узнать свой вес. Но шкала весов до 20 килограммов была повреждена и показания по ней прочитать не представлялось возможным. Поэтому Винни-Пух взвесился сначала с Кроликом: получилось 22,4 кг; затем с Пятачком, получилось 23,5 кг; а затем они взвесились все вместе получилось 26,7 кг. Какова масса каждого из них в отдельности?
Древнеиндийская задача.
Есть кадамба-цветок.
На один лепесток
Пчелок пятая часть опустилась.
Рядом тут же росла
Вся в цвету сименгда,
И на ней третья часть поместилась.
Разность их ты найди,
Её трижды сложи,
На кутай этих пчел посади.
Лишь одна не нашла
Себе места нигде,
Все летала то взад, то вперёд и везде
Ароматом цветов наслаждалась.
Назови теперь мне, подсчитавши в уме,
Сколько пчелок всего здесь собралось?
Ответ: 15 пчёл
Задание 3. Отгадай пословицу
Выполните действия:
1-й ряд
1,4+0,6
2-1,7
2-й ряд
2,6+0,4
3-2,8
0,3∙1,2
0,36+0,04
0,4+0,96
1,36-0,2
1,16∙0,5
0,58∙50
29-27,84
1,16-0,86
0,2∙1,8
0,36-0,33
0,03+0,97
1-0,1
0,9∙0,5
0,45+0,9
1,35-0,99
0,36∙50
Ключ
1-й ряд
| 0,4 | 1,36 | 2 | 1,16 | 0,3 | 29 | 0,36 | 0,58 |
| ч | и | к | л | о | е | н | д |
2-й ряд
| 0,2 | 3 | 1 | 0,03 | 0,45 | 0,9 | 1,35 | 0,36 | 18 |
| у | г | и | я | м | с | е | л | о |
- связанных с русским языком:
Задание. Известно, какое значение имеет запятая в руссом языке. От неправильной расстановки запятых смысл предложения может резко измениться. Например, «Казнить, нельзя помиловать», «Казнить нельзя, помиловать». В математике от положения запятой зависит верность или неверность равенства. Расставьте в следующих забавных равенствах запятые:
32+18=5
736-336=4
14∙5=7
63-27=603
3+108=408
12∙50=60
- связанные с биологией:
Задание. Расшифруйте название многолетнего растения, встречающегося, в Мексике, которое цветет один раз в жизни (примерно на 40-60 год своего существования), после чего сразу же отмирает. Для этого сократите дроби. В кружках впишите буквы, соответствующие найденным ответам.
| 3/5 | 2/3 | 4/5 | 6/9 | 4/7 |
| а | г | в | у | т |
9/15 =
12/18 =
24/40 =
28/35 =
21/35 =
- связанные с географией:
Задание. Расшифруйте название высочайшей горной вершины мира.
Для этого представьте в виде десятичных дробей заданные числа и впишите в таблицу буквы, соответствующие найденным ответам.
У =
О =
Г =
Н =
М =
А =
Ж =
Л =
Д =
| 0,14 | 0,15 | 0,5 | 0,4 | 0,5 | 0,16 | 0,2 | 0,75 | 0,25 | 0,4 | 0,125 |
Знаете ли вы другое название этой вершины?
Вычислите её высоту (в метрах):
1002-0,5∙2308=
Ответ:_______________________________________________________.
- упражнения направленные на развитие творчества и логического мышления учащихся:
Задание 1. Восстановить запись:
Решение. Так как сумма дробей равна целому числу, то А=5, так как сумма — пятизначное число, а целые части — четырехзначные, то Б=1, а С=7. У и К — цифры, большие 5, перебором находим решение.
Задание 2. В пустые клетки квадрата вписать дроби так, чтобы по любой горизонтали, вертикали и диагонали сумма чисел была равна 3.
| 1,3 | 0,6 | 1,1 |
| 0,8 | 1 |
|
| 0,9 |
|
|
Задание 3. Решите примеры. Используя ответы, прочитайте текст «Математические термины». Для этого запишите в таблицы буквы, соответствующие найденным ответам.
Ш 2,1 · 1/3 = О 2/3 : 1 1/3 =
Н 3,5 · 2/7 = Я 0,5/0,3 =
Й 4.8 · 3/8 = Ц 7/25 : 2 =
Т 2,04 : 1/5 = Р 0,5 : 5/6 =
И 4 3/11 : 9 - 4 3/11 · 1/9 = П (0,8 + 0,2) : 5/6 =
Е 3/4 : 3 – 0,2 =
Известно, что результат при делении называется ____________. Однако, нередко для обозначения этого результата используется слово
| 1/2 | 10 1/5 | 1 | 1/2 | 0,7 | 0,05 | 1 | 0 | 0,05 |
В математике, при решении некоторых задач приходится иметь дело с равенствами, составленными из двух
| 0,5 | 10,2 | 1 | 0,5 | 0,7 | 1/20 | 1 | 0 | 1 4/5 |
Такие равенства называют
| 1 1/5 | 0,6 | 1/2 | 1,2 | 1/2 | 3/5 | 0,14 | 0 | 1 2/3 |
Задание 4
а) Один велосипедист за 0,3 часа проезжает 5,4 км, а другой за 0,4 часа проезжает 6,6 км. Кто движется быстрее?
б) Одна швея за 3 часа шьет 4 фартука, а вторая — за 5часов 7 фартуков. У кого из них выше производительность?
Гуманитаризация школьного математического образования предполагает также использование различных видов уроков: от классического до нестандартного.
При проведении традиционных уроков в их содержание можно включать задания приведенные выше, а также оригинальное начало, литературное вступление в стихах и т.д.
Например, вступительное слово учителя при решении практических заданий: «Решение задач — практическое искусство, подобное плаванию, катанию на лыжах или игре на фортепиано, научиться ему можно «Если вы хотите плавать, смело входите в воду, а если хотите научиться решать задачи, то решайте их», — советовал учащимся известный американский математик Джорж Пойа в книге «Как решить задачу». Решение любой достаточно трудной задачи требует напряженного труда, воспитывает волю, упорство, развивает любознательность, смекалку. Это очень нужные качества в жизни человека, ведь даже в пословице говорится: «Ум без догадки гроша не стоит».
Или же вступление в стихах:
Дикобраз в подарок сыну
Сделал счетную машину.
К сожалению, она
Недостаточно точна.
Результаты перед вами,
Быстро все исправьте сами.
Далее следует серия неверно решенных примеров на арифметические действия с дробями.
Нестандартные уроки — это уроки проводимые в игровой форме: занятия с элементами игры, соревнования, содержащие игровые ситуации.
Игры и игровые формы должны включаться не для того, чтобы развлечь учащихся, а удачно соединить игровые и учебные мотивы и постепенно сделать переход от игровых мотивов к учебным, познавательным.
В качестве таких уроков можно использовать уроки приведенные в приложениях 1 и 2.
Заключение
В работе были рассмотрены основные положения и принципы технологии гуманитаризации, приведены некоторые рекомендации по её применению. Был рассмотрен гуманитарный потенциал некоторых основных учебников по математике, среди которых в этом отношении особо выделяется учебник Дорофеева.
Внедрение элементов технологии гуманитаризации может проводить каждый учитель, обладающий творческим потенциалом, любящий свой предмет и относящийся к ученикам как субъектам обучения. Но чтобы правильно строить процесс обучения, учителя всегда должны помнить, что человеческое мышление изначально двустороннее: логическая и эмоционально-образная стороны существуют как равноправные части.
По мнению психологов, для того, чтобы системность работы двух полушарий человеческого мозга была обеспечена, т.е. чтобы мы имели всесторонне-развитую личность, нужен баланс между знаково-цифровой (математика, физика и т.п.) и образной (литература, музыка, живопись и т.п.) информацией.
В наше время, когда рост знаковой функции идет «семимильными шагами», баланс может нарушаться. В результате угнетенности эмоционально-образной сферы и происходят перекосы в нашем обществе. А это опасно, так как наши чувства определяют первые «движения души»; желания формируют действия; логика уже «постфактум» пытается теоретически оправдать наши действия.
Чтобы потом не сокрушаться о невосполнимом, нужно пытаться, по возможности, решать задачи в стихах, включать стихи в правила (возможно, для многих учеников это лучший способ его запомнить), ставить инсценировки, создавать проблемную ситуацию на уроке, находить места, где уместен музыкальный фон.
Для более полноценного внедрения технологии гуманитаризации в практику школы, необходимы соответствующая учебно-методическая литература с достаточным гуманитарным потенциалом.
Практическое применение элементов технологии гуманитаризации показало, что у учащихся повышается интерес к предмету и обучению как виду деятельности вообще. Исследования проведенные в данной работе могут послужить практическим приложением для учителей математики, побудить к поиску новых эффективных путей внедрения элементов технологии гуманитаризации и гуманитаризации предмета вцелом.
Библиографический список
Беспалько В.П. Слагаемые педагогической технологии М., Педагогика, 1989г.
Виленкин Н. Я. уч-к «Математика» 5-6 кл.- М.: «Сайтком » 2000 г.
Виленкин Н. Я., Депман И. Я. «За страницами учебника математики» - М.: «Просвещение», 1989 г.
Лихачев Б. Т. «Педагогика» - М.: «Прометей»,1993 г.
Мацеевский В. А. «Очерк истории письменности и просвещение славянских народов до 14 века» - М.: «Просвещение»,1946 г.
«Оценка качества занятий по математике» - М: «Дрофа»,2000 г.
«Программно методические материалы по математике. Тематическое планирование 5 – 6 класс» - М.: «Дрофа», 1999 г.
Полякова Т. С. «История отечественного школьного математического образования» - Издательство РГПУ,1997 г.
Полякова Т. С., Кондрашова З. И., Герасимова О. С. «Гуманитаризация школьного образования использование литературы в обучении математике», - издательство РГПУ , 1997 г.
Саввина О. А. ст-я «Эстетический потенциал истории математики» ж-л «Математика» №3 2001 г.
Савин А. П. «Я познаю мир. Математика», - М.: АСТ 1998 г.
Саранцев Г. И. ст-я «Методика обучения математике на рубеже веков» ж-л «Математика» №7 2000 г.
Симонов Р. А. «Математическая мысль Древней Руси» - М., «Наука», 1977 г.
Симонов Р. А. «Русская средневековая система больших чисел» - М., 1970 г.
Симонов Р. А. «О связи древнерусского обозначения больших чисел с вычислительной практикой» - М., «Наука», 1975 г.
Тонких А. Б. «Логические игры и задачи на уроках математики» - Ярославль: «Академия развития», 1997 г.
Финько З. ст-я «Игровые уроки» - ж-л «Математика» №23 2001 г.
Халилова Т. ст-я «Современные идеи гуманитаризации образования на уроках математики» - ж-л «Математика» №48 2000 г.
Приложение 1
«Гуси-лебеди и обыкновенные дроби» Урок-игра
Цель: 1. Закрепить навыки сравнения дробей, умения складывать и вычитать дроби с одинаковыми и различными знаменателями, находить дробь от числа.
Похожие работы
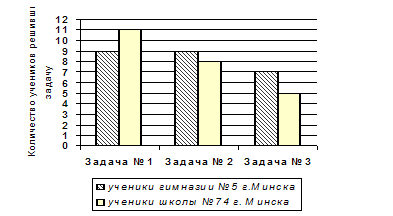
... № 5 при решении задач выше, чем у учеников средней школы № 74. Итак, результаты эксперимента подтверждают гипотезу о том, что, если при обучении математике младших школьников использовать образовательную программу “Школа 2100” (деятельностный метод), то процесс обучения будет более продуктивный и творческий. Подтверждение этому, мы видим в результатах решения задач № 4 и № 5. Ученикам ранее не ...
... в психологии. Воспитательные аспекты обучения математике раскрываются в соответствии с концепциями развития личности, которые разработаны в психологии и педагогике. Можно говорить о том, что методика обучения математике как научная область должна иметь такую же структуру, как и любая другая наука, т.е. она должна состоять из отдельных научных теорий. Каждая из них имеет один и тот же объект — ...
... урок занимает определенное место в системе учебного предмета, при изучении конкретной школьной дисциплины. Структура урока воплощает закономерности и логику процесса обучения. 2. Типы уроков и система приемов учебной деятельности в обучении математике Существуют различные типы уроков в современном учебном заведении. 1. Комбинированный урок (наиболее распространенный тип урока в массовой ...
... лет - ребенок твой бог, с трех до десяти- он твой раб, с десяти лет - ребенок твой друг» (древнекитайская мудрость). 3 Гуманизация и гуманитаризация образования – социальная проблема Общеизвестно, что образование — обучение и воспитание, но не всем известно, в чем заключается философия образования, складывавшаяся веками. Философия всегда стремилась не только осмыслить существующие системы ...



0 комментариев