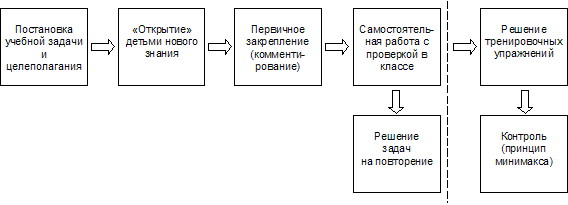
Навигация
Развивать вычислительные навыки учащихся, логическое мышление, математическую речь
2. Развивать вычислительные навыки учащихся, логическое мышление, математическую речь.
3. Воспитывать чувства сопереживания.
Ход урока
Урок начинается с того, что учитель приглашает ребят в волшебный мир сказок. Но вот по какой сказке они будут путешествовать, ребята должны догадаться сами. В качестве подсказки каждому выдается набор карточек. На карточках нарисованы какие-то линии и дроби. Нужно выложить карточки так, чтобы дроби расположились в порядке возрастания. В каждом наборе – карточки разных форм и рисунки у всех неодинаковые, но, выложив эту мозаику, учащиеся обнаруживают, что у всех получились изображения лебедей.
Сразу вспомнилась сказка «Гуси – лебеди». Утащили гуси – лебеди, а его сестрица бросилась их догонять. Бежала – бежала и видит: течет речка. Попросила девочка речку пропустить ее, а та и говорит: «Угадай мои загадки, тогда пропущу». Давайте и мы с вами, ребята, попробуем разгадать загадки речки.
Вопросы речки (их можно прочитать на фоне журчания воды, записать на магнитофон и включить запись в нужный момент):
1. Если у моего истока пустить бумажный кораблик, то к устью он доберётся через 22 800 с. Сколько минут и сколько часов будет плыть кораблик?
2. Бумажный кораблик проплывёт от моего истока 2 2/3ч. Сколько часов ему осталось плыть до устья?
3. На моём пути я теку по-разному, то медленно, то быстро. Вот, например, иногда мне приходится увеличивать скорость на 3 1/6км/ч и она становится равной 4 5/6км/ч. Какой же в таком случае была моя скорость первоначальной?
4. Я теку по лесу10 км, что составляет 2/3 от всего моего пути от истока до устья. Как велик этот путь?
Ответы на вопросы речки ребята записывают в своих тетрадях, а потом проверяют себя по готовым ответам на доске.
Итак, сестрица вместе с нами ответила на вопросы речки, и позволила ей перейти на другой берег. Девочка побежала дальше. И вдруг видит: стоит печка. Девочка спросила её, куда полетели гуси-лебеди. А печка отвечает:
«Милый дружок, съешь пирожок, укажу путь». На доску проецируется изображение пирога состоящего из четырёх частей. На каждой доле указана её масса. Может ли девочка одна съесть такой пирог? Подсчитайте его массу. Давайте поможем девочке съесть этот пирог. Подсчитайте, сколько вас и сколько граммов пирога придётся на каждого, если вы будете его есть вместе с девочкой.
Печка указала девочке путь, но только до яблоньки. А та вся согнулась под тяжестью яблок и умоляет собрать хоть часть урожая. А девочка торопится и хочет справиться с работой как можно быстрее. Но для этого ей надо ответить на следующие вопросы яблоньки:
1. Всего на мне уродилось 60 яблок. Я прошу сорвать только 7/15 моего урожая. Сколько яблок нужно сорвать?
2. Когда гуси – лебеди остановились отдохнуть под моими ветвями, твой братец сорвал ¼ того, что ты сейчас собрала. Сколько яблок он сорвал?
3. Я готова подарить часть своего урожая, но хочу, чтобы у меня осталась 1/10 его часть. Сколько яблок всего нужно сорвать, чтобы я была довольна?
Наконец собрано нужное количество яблок и дорога указана. Девочка прибегает к избушке Бабы-яги, куда гуси-лебеди утащили братца. А Баба-яга оказалась строгой. Она не хочет отдавать мальчика, коли за ним так плохо следили, что позволили гусям утащить его. Баба-яга говорит девочке: «Вот ты и твои друзья-ученики сначала покажите, как вы умны и внимательны. Я буду задавать вам трудные вопросы, а вы отвечайте. Ответите – забирайте братца. Не ответите – ступайте доучиваться, а только тем, кто не хочет учиться, я ребёнка не доверю».
Давайте поможем девочке и ответим все вместе на заданные вопросы. (Самостоятельная работа.)
1. Изобразите на координатной прямой числа: ½, 1 1/3, 2 1/6. ( За единичный отрезок примите шесть клеток.)
2. Выполните действие: 10 2/3 – 7; 7 5/7 + 4 3/7; 5 – 3 3/8.
3. Установите, что больше: ¾ или1? 1/6 или1/7? 10/7 или1?
4. Между какими соседними натуральными числами находится число 6 2/3? Запишите ответ в виде двойного неравенства.
Тетради учащихся учитель в конце урока забирает на проверку.
Приложение 2
Урок-путешествие
по теме «Совместные действия с обыкновенными и десятичными дробями»
Цели: 1) непринуждённо и ненавязчиво повторить тему «Совместные действия с обыкновенными и десятичными дробями»;
2) развивать вычислительные навыки, логическое мышление, речь, память учащихся;
3) воспитывать чувства коллективизма, взаимопомощи, сопереживания.
Ход урока
В начале урока учитель объявил: «Сегодня занятие будет необычным. Мы совершим увлекательное путешествие в поисках сокровищ. Но сначала надо проверить, готовы ли мы отправиться в путь, хорошо ли мы вооружены знаниями?».
Задания
1. Прочитайте дроби:
1,2; ; ; 0,04; ; 1,875; .
Укажите среди них: обыкновенные, десятичные.
Чем различается запись десятичных и обыкновенных дробей?
Что показывают числитель и знаменатель обыкновенной дроби?
Какая обыкновенная дробь называется правильной? неправильной?
2. Обратите данные обыкновенные дроби в десятичные, а десятичные — в обыкновенные:
0,1; 1,6; ; ; ; 5.
3. Сравните числа:
и 0,4; и 0,2; и 2,25.
4. Назовите числа, обратные и противоположные данным:
; ; ; 0,3; 12; 1,05.
Чему равна сумма противоположных чисел?
Чему равно произведение взаимно обратных чисел?
5. Сравните с единицей сумму дробей:
++; +0,2+.
Устная фронтальная работа класса продолжается в ходе составления карты путешествия. Составление карты идёт так же, как игра в лото. На доске заранее укреплён большой лист ватмана, разделенный на шесть равных частей. На каждой части крупно нарисовано число (оно будет фигурировать в ответах к математическому лото). А на столе учителя лежат тыльной стороной вверх шесть квадратов таких же по размерам, как и квадраты на вывешенном разграфленном листе. На каждом квадрате с лицевой стороны нарисован участок карты, а на тыльной — одно из шести чисел, изображенных на разграфленном листе.
Задания
(Математическое лото)
Выполните действия:
; ; -2 : (-2); ; 0,4 · ; .
Учащиеся выполняют задания, а затем учитель медленно и в разбивку объявляют ответы: -2,5; 0,1 и т.д. Тот учащийся, кто первым заявил, что в его работе есть объявленный ответ, вызывается к доске и прикрепляет квадрат с таким же числом, как и в его ответе к тому месту на ватмане, где увидит то же число, что и на квадрате. Постепенно складывается карта (рис. 1).
Учитель завершает этот этап урока словами: «Итак, карта у нас есть, настроение отличное. В путь! С песней!». Звучат строки из песни «Ничего на свете лучше нету» (только первый куплет):
Ничего на свете лучше нету,
Чем бродить друзьям по белу свету.
Тем, кто дружен, не страшны тревоги,
Нам любые дóроги дорóги.
Нам любые дóроги дорóги.
Начиная с этого момента, у ребят перед глазами находится карта. На ней видны все этапы путешествия.
Прежде всего, мы очутились на поляне цветов. Но их красота обманчива. Среди них есть ядовитые и целебные. Наша задача не ошибиться, когда будем собирать букет.
На доске мелом нарисованы цветы (Рис. 2), их сердцевины пронумерованы, а на лепестках написаны дроби. Эти дроби надо перемножить и ответ сверить с дробью, записанной на листочке цветка. Если ответы совпадут, то цветочек целебный, если нет — ядовитый.
Дети дают ответы при помощи сигнальных карточек. У каждого ученика на парте лежат красная и зеленая карточки. Если цветок ядовитый, то поднимают красную карточку, если целебный – зеленную. Вслух ничего не произносят.(дроби подобраны так, чтобы две из трех были взаимно обратными. Так закрепляется правило умножения взаимно обратных чисел.) Все вместе устанавливают, что цветы 1, 3, 4 – целебные, а 2 и 5 – ядовитые.
После цветочной поляны мы попали на перепутье. По какой дороге идти? Об этом узнаем, если выполним задания. Их три – по одному для каждого ряда. Задания уже записаны на доске. Обязательное условие: ответ записать в виде десятичной дроби и округлить до единицы.
Задания
1. 2. 3.
Ребята делают расчеты на своих местах, а трое учеников – у доски. Получаются ответы:
1. 0,64 ≈ 1;
2. 0;
3. 0,040. ≈ 0.
Учитель объясняет, что ноль в ответе означает тупик, которым кончается дорога. Итак, дороги № 2 и 3не приведут нас к цели. Значит, надо идти по дороге № 1 .
По карте видно, что мы подошли к озеру. Наловим рыбки для ухи.
На доске написаны пять заданий, которые закрыты листами бумаги, чтобы заранее дети их не увидели. На учительском столе разложены пять крупных рыб (рис. 3), вырезанных из бумаги.
На каждой рыбке проставлен номер (это номер задания). Голова рыбы унизана скрепками. Берем «удочку», на конце лески прикреплен магнит. Магнит «цепляет» скрепки – и рыбка поймана. По её номеру становится ясно, какое задание открывать для решения.
Задания
1. На какое число надо разделить 2, чтобы получить 4?
2. Меньше или больше половины литровой банки наполнится водой, если в нее влить: л; 0,7 л; л?
3. Вычислите
4. Найдите сумму четырех десятых числа 40 и двух третей числа 36.
Поудив рыбу и сварив воображаемую уху, мы подходим к мельнице. Вблизи (рис. 4) она, конечно, значительно больше, чем на карте. Теперь мы можем рассмотреть её во всех подробностях. Мельница перемалывает все описания числа, начиная с середины (это число 4,5). Пойдем и мы вслед за стрелками на рис. 4, выполняя то действие, которое записано на стрелке. Получив ответ, двигаемся дальше. Например:
4,5-=→+5→5-2,7=2,3. И тд.
Найдя окончательный ответ, ребята продолжают путь, но тут начинается буря (учитель включает магнитофон, и раздаются звуки сильного ветра и потоков дождя). Мы вымокли, ветер пронизывает, озябли. С надеждой смотрим на карту и с радостью замечаем, что можем укрыться в пещере. Что мы и делаем. А погода испортилась, видимо, на несколько дней. Сколько же мы сможем продержаться здесь? Ответ на этот вопрос мы найдем, решив задачу про пещеру, воду и …проценты.
Задача. В пещере обнаружено 750 л пресной воды. На сколько дней хватит этого запаса воды для 30 человек, если один человек в день расходует 0,2 % от всего количества воды?
Сначала разбираем решение всем классом, а затем один ученик делает записи на доске:
1) 0,2 % = ;
2) 750 : 1000 ∙ 2 = 1,5 (л) — столько воды расходует один человек в день;
3) 1,5 ∙ 30 = 45 (л) воды расходуют 30 человек в день;
4) 750 : 45 = (дней) — столько дней будет расходоваться запас воды в пещере.
Интересно обсудить с ребятами вопрос об округлении результата. Во-первых, нужно ли округлять число ? — Нужно, поскольку в задаче требуется узнать целое число дней. Во-вторых, как округлять? Лучше рассуждать не формально. Так, если нам хватило воды на две трети дня, то, значит, в этот день мы без воды не остались. Тогда ответ должен быть таким: воды хватит на 17 дней. Подчёркиваем, что рассуждая строго по правилу , мы придём точно к такому же результату.
Буря кончилась, мы выходим из пещеры на лесную поляну. Здесь отдохнём. Можно расслабиться, пошутить, почитать стихи. Несколько человек приготовили на подарок — выучили стихотворение В. Лившица «Три десятых» и теперь читают его нам по четверостишьям:
Это кто из портфеля швыряет в досаде
Ненавистный задачник, пенал и тетради?
И суёт свой дневник, не краснея при этом,
Под дубовый буфет, чтоб лежал под буфетом?
Познакомьтесь, пожалуйста, Костя Жигалин,
Жертва вечных придирок, — он снова провален.
И шипит, на растрепанный глядя задачник:
— Просто мне не везёт! Просто я неудачник!
В чем причина обиды его и досады?
Что ответ не сошелся лишь на три десятых!
Это сущий пустяк, и к нему, безусловно,
Придирается строгая Марья Петровна.
Три десятых. Скажи про такую ошибку,
И, пожалуй, на лицах увидишь улыбку.
Три десятых… И всё же об этой ошибке
Я прошу вас послушать меня без улыбки.
Если б, строя ваш дом, тот, котором живете,
Архитектор немного ошибся в расчете —
Что б случилось, ты знаешь ли, Костя Жигалин?
Этот дом превратился бы в груду развалин!
Ты вступаешь на мост, он надёжен и прочен,
А не будь инженер в чертежах свои точен,
Ты бы, Костя, свалившись в холодную реку,
Не сказал бы спасибо тому человеку!
Три десятых — и стены возводятся косо!
Три десятых — и рухнут вагоны с откоса!
Ошибись только на три десятых аптека —
Станет ядом лекарство, убьёт человека…
Ты подумай об этом, мой друг, хладнокровно,
И скажи — не права ль была Марья Петровна?
Если честно подумать, Костя, об этом,
То не долго лежать дневнику под буфетом!
На отдыхе можно и шутливые задания выполнять. Например:
Одновременно написать на доске число 7,2 левой рукой, и число 2,7 — правой.
С завязанными глазами записать и выполнить задание на сложение двух десятичных дробей, обыкновенной и десятичной.
Отдохнув, мы двигаемся далее и вот, наконец, дошли до того места, где зарыт клад. Но нам преграждает путь дракон. Его появление было предсказано картой, но он всё-таки возникает неожиданно.
Плакат с нарисованным на нем цветным драконом (Рис. 5) укреплен на обратной стороне подвижной створки доски. Учитель открывает створку, и все видят «страшное» чудовище. Каждая голова дракона держит листок с заштрихованным словом, где известны только первая и последняя буквы.
Угадав все слова, ребята повергают чудовище в прах.
Вот теперь наступает самая волнующая минута. Можно взять клад! И тут учитель из «тайника» достает ларец (стилизованный под старину), медленно его открывает. Напряжение в классе растёт: все видит много-много старинных золотых монет. На самом деле — это маленькие круглые шоколадки в золотой фольге, но дети не думают об этом. Они честно делят клад друг с другом и весело поедают свою законную добычу.
Похожие работы
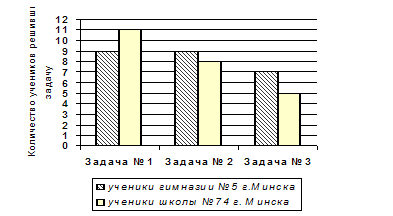
... № 5 при решении задач выше, чем у учеников средней школы № 74. Итак, результаты эксперимента подтверждают гипотезу о том, что, если при обучении математике младших школьников использовать образовательную программу “Школа 2100” (деятельностный метод), то процесс обучения будет более продуктивный и творческий. Подтверждение этому, мы видим в результатах решения задач № 4 и № 5. Ученикам ранее не ...
... в психологии. Воспитательные аспекты обучения математике раскрываются в соответствии с концепциями развития личности, которые разработаны в психологии и педагогике. Можно говорить о том, что методика обучения математике как научная область должна иметь такую же структуру, как и любая другая наука, т.е. она должна состоять из отдельных научных теорий. Каждая из них имеет один и тот же объект — ...
... урок занимает определенное место в системе учебного предмета, при изучении конкретной школьной дисциплины. Структура урока воплощает закономерности и логику процесса обучения. 2. Типы уроков и система приемов учебной деятельности в обучении математике Существуют различные типы уроков в современном учебном заведении. 1. Комбинированный урок (наиболее распространенный тип урока в массовой ...
... лет - ребенок твой бог, с трех до десяти- он твой раб, с десяти лет - ребенок твой друг» (древнекитайская мудрость). 3 Гуманизация и гуманитаризация образования – социальная проблема Общеизвестно, что образование — обучение и воспитание, но не всем известно, в чем заключается философия образования, складывавшаяся веками. Философия всегда стремилась не только осмыслить существующие системы ...



0 комментариев