Навигация
3 класс.
В результате осуществления предложенных изменений в порядке прохождения учебного материала значительно облегчается программа третьего года обучения, за счёт создания прочной базы обобщённого восприятия многих вопросов, составляющих содержание учебного материала третьего года обучения.
Обоснованный подход к структурированию материала высвобождает дополнительное время для изучения таких трудных для детей вопросов, как деление на многозначное число, а также для возвращений к тем вопросам программы начальной школы, которые оказались усвоены недостаточно полно и глубоко.
Основные положения данной рекомендации, разработанные автором И.И.Аргинской, должны быть положены в основу работы учителя классов коррекции, но учитель должен осуществлять к организации учебного процесса своего класса творческий подход и структурировать учебный материал в соответствии с особенностями своих учеников (физиологических, психических, психолого-педагогических).
2. Методика обучения математике в коррекционных классах, направленных на развитие математических способностей учащихся.
Обучение в классах коррекции – это прежде всего дифференцированный процесс. Обучение в каждом конкретном классе индивидуально и зависит от состава класса. Поэтому учителя, работающие в этих классах, творчески подходят к методике обучения и зачастую некоторые особенности методики носят индивидуальный характер.
* * *
Рассмотрим некоторые фрагменты уроков
А) с геометрическим материалом;
Б) с арифметическим материалом;
В концентре «Сотня I кл» ребят знакомят с геометрическими понятиями: прямая, луч, отрезок. Вот как возможно это сделать, используя сказку «Путешествие точки по стране геометрии» .
Фрагменты урока-знакомства с геометрическими понятиями: прямая, луч, отрезок.
- Жила-была точка. Вот она (на магнитную доску вывешивается модель точки).
- Она была очень любопытная и хотела всё знать. Увидит незнакомую линию и непременно спросит: «Как эта линия называется?»
- А какие вы, ребята, знаете линии? (Кривые, прямые, ломаные).
- Подумала однажды точка: «Как же я смогу всё узнать, если всегда буду жить на одном месте?! Отправлюсь-ка я путешествовать!». Сказано-сделано (на доске прямая). Вышла точка на прямую и пошла по этой прямой (учитель передвигает по этой прямой точку). Шла-шла по прямой линии. Долго шла. Устала. Остановилась и говорит: «Долго ли я ещё буду идти? Скоро ли конец прямой?» Засмеялась прямая: «Эх ты, точка! Ведь ты не дойдёшь до конца. Разве ты не знаешь, что у прямой нет конца?»
- «Тогда я поверну назад»,- сказала точка. «Я, наверное, пошла не в ту сторону».
- «И в другую не будет конца. У прямой линии совсем нет концов».
- А вы, ребята, где в жизни могли видеть прямую без конца и без края? (Рельсы, провода). Посмотрите, и наша прямая не имеет конца. Я могу её продолжить (учитель показывает). Давайте начертим прямую у себя в тетради, только вся она у нас не поместится, начертим её часть. А что же наша точка?
- «Как же быть?»,- спрашивает она. «Что же мне так и придётся идти, идти и идти без конца?».
- «Ну, если ты не хочешь идти без конца, давай позовём на помощь ножницы»,- сказала прямая.
- «Давай позовём. А зачем нам ножницы?».
- «Сейчас увидишь». Тут, откуда ни возьмись, появились ножницы , щёлкнули перед самым точкиным носом и разрезали прямую (учитель имитирует разрезание прямой).
__________________| |________|_____________
- «Ура!»,- закричала точка. «Вот и конец получился! Ай, да ножницы! А теперь сделайте, пожалуйста, конец с другой стороны.
- «Можно и с другой»,- послушно щёлкнули ножницы.
______________| |_________|__________| |__________________
- «Как интересно!»,- воскликнула точка.
- «Что же из моей прямой получилось? С одной стороны конец, с другой стороны – конец. Как это называется?»
- «Это отрезок»,- сказали ножницы. «Теперь ты, точка, на отрезке прямой».
- «Отрезок прямой, отрезок прямой»,- с удовольствием повторила точка, прогуливаясь по отрезку от одного конца до другого.
- Давайте и мы начертим в тетради две точки. Приложите к ним линейку и соедините точки прямой линией. Получился отрезок. Начертите ещё отрезки. (ученики чертят разные отрезки: по длине, расположению на листе). К доске вызываются ученики начертить свой отрезок.
Хором повторяют название – «отрезок».
- Я запомню, - сказала точка,- это название. Мне нравится на отрезке! Но прямая мне тоже нравится. Жаль, что её не стало. Ведь теперь вместо прямой есть мой отрезок и ещё два этих…. - не знаю как их назвать. Тоже отрезки? (Как вы, ребята, думаете?- Нет. У отрезка 2 конца).
- Нет,- ответили ножницы. Ведь у них конец только с одной стороны, а в другую сторону нет конца. И называется это по-другому.
- А как они называются?
- Лучами.
Это луч. И это луч. ____________________| |______________________
- А! – радостно сказала точка. – Я знаю почему они так называются. Они похожи на… (А кто скажет на что похожи эти лучи?) – солнечные лучи.
- Да, - подтвердили ножницы. Солнечные лучи начинаются на солнце и идут от солнца без конца, если только не встретят что-нибудь на своём пути. Например, Землю, Луну или спутник.
- Значит из прямой вот что получилось: мой отрезок и ещё два луча. Давайте и мы начертим лучи у себя в тетради.
- Скажите, чем же отличаются и что общего между прямой, отрезком и лучом? (общее – все прямые). Отрезок и луч имеют конец, только отрезок – два конца, а луч – один. У прямой конца совсем нет.
Далее следуют задания на закрепление.
Теперь рассмотрим фрагмент урока на арифметический материал.
Тема: «Сложение и вычитание двузначных чисел, оканчивающихся на 0».
(40+20);(50-30)
На доске десятки (полоски, содержащие 10 квадратов)
40+20
Учитель на доску выкладывает 4 полоски.
Учитель: сколько десятков на доске?
Ученик: четыре.
Учитель: какое это число?
Ученик: 40.
Учитель добавляет ещё 2 полоски в другую сторону доски.
Учитель: Добавлю ещё десятки. Сколько на доске?
Ученик: 2.
Учитель: какое число?
Ученик: 20.
Учитель: а теперь нам нужно узнать сколько десятков и тут (показывает на 4 десятка) и тут (на 2 десятка) вместе. Как это сделать?
Ученик: сложить 4 десятка и 2 десятка.
Учитель: записывает 4 десятка+2 десятка=6 десятков
40+20=60. Что общего в числах 40,20,60?
Ученик: 0 – единиц.
Учитель: Я могу ещё по-другому записать этот пример - в столбик. Посмотрите, как я это делаю. Пишу десятки под десятками, единицы под единицами. Складываю. Начинаю с единиц. Складываю единицы: 0 единиц+0 единиц=0 единиц. Складываю десятки: 4 десятка+ 2 десятка= 6 десятков. Читаю ответ: шестьдесят.
Аналогичный приём используется при сложении двузначных чисел, из которых одно оканчивается 0, 34+20 и сложение двузначного и однозначного числа 34+2. А также при сложении и вычитании двузначных чисел без перехода через десяток (например, 42+53, 28-12).
Иная запись в столбик используется при сложении двузначного числа с однозначным и двузначного с двузначным с переходом через десяток. Например, 26+4. Пишу десяток под десятком, единицу под единицей.
Пишу 4 под 6. Складываю единицы, 6+4=10. Записываю 10. Под десятком переписываю 2. Складываю. Получаем 30. Такая запись в столбик оформляется для того, чтобы избежать ошибок при получении двузначного числа в результате сложения единиц и перехода десятка в свой разряд. (Этот десяток забывается детьми).
Приведём ещё пример:
Пишу десяток под десятком, единицу под единицей. Складываю единицы. 9+3=12. Записываю 12. Складываю десятки 4+2=6. Записываю под десятками 6. Складываю. Ответ: 72.
Заметим, что письменно выполнение действий быстро и хорошо усваивается детьми и , вскоре, многие из них переходят у устным вычислениям.
Для того, чтобы у детей закрепились правила в памяти нужно чаще повторять уже ранее изученный материал. Это правило поможет и в дальнейшей работе учителя.
* * *
Описание и результаты эксперимента.
Эксперимент проводился нами в школе №40 в 1б классе коррекции, учителя Дуюновой С.А. В классе 12 детей.
Экспериментальная работа велась в направлении: сравнение результатов успеваемости учащихся одного и того же класса в конце учебного года 1 класса и в начале учебного года 2 класса.
Для проведения эксперимента были подобраны идентичные задания, которые проводились в конце четверти после работы над задачами по предлагаемой методике. Учащимся класса коррекции были предложены задачи типа:
I. Распознавание задачи.
Отметь те задания, которые являются задачами.
1) На столе лежали фрукты: яблоки и груши.
2) На столе лежали 2 яблока и 6 груш. Сколько на столе яблок?
3) На столе лежат 2 яблока, а груш на 3 больше. Сколько груш лежат на столе?
4) На столе лежат 5 фруктов, из них 2 яблока.
II. Решение простых задач.
Поставь все возможные вопросы и реши задачи.
1) В сборнике 10 стихов и 8 рассказов.
2) В вольере 11 попугайчиков, а канареек на 3 больше.
III. Поставь к условию задачи вопрос так, чтобы задача получилась на сравнение.
У Оли 15 марок, а у Нины – 8.
Критерием оценки служат уровни.
1) Высокий уровень: задачи выделены верно, предложены более двух вопросов.Ученик справился с заданиями на отлично. Учебный материал ребёнком усваивается легко, полно овладевает программой.
2) Средний уровень: у ребёнка есть ошибки в выполнении заданий, ошибки в решении. Но в основном ребёнок усвоил то, что нужно было сделать. Ребёнок усваивает основное в программе, понимает учебный материал.
3) Низкий уровень: ребёнок не справился с заданиями, не усвоив программу.
В ходе эксперимента были достигнуты следующие результаты:
4 человека с высоким уровнем успеваемости (33%)
4 человека со средним уровнем успеваемости (33%)
4 человека с низким уровнем успеваемости (33%)
Эксперимент не закончен и будет продолжен в следующем году.
Заключение.
1. Возникла необходимость обучать детей группы риска в классах коррекции, организованных в структуре общеобразовательных школ, используя специальную методику проведения уроков математики.
2. Психолого-педагогические особенности детей группы риска, отличающие их от сверстников, требуют пересмотра подхода к обучению в этих классах, используя специфические методики обучения.
3. Учебная деятельность в классах коррекции организуется в форме дифференцированного подхода к учащимся. Обучение в таких классах с учётом сохранных интеллектуальных возможностей группы риска ведётся по действующим в классовой школе программам, с опорой на действующие учебники.
4. Материал работы может быть полезен студентам, учителям начальной школы и практическим работникам народного образования.
Литература.
1. Андрущенко Т.Ю., Карабекова Н.В. Коррекция психического развития младшего школьника на начальном этапе обучения. Вопросы психологии 1993 №1.
2. Актуальные проблемы диагностики задержки психического развития детей. Под ред. К.С. Лебединской, М: Педагогика, 1982.
3. Аргинская И.И., Дмитриева Н.Я., Полякова А.В., Романовская З.И. Обучаем в системе Занкова Л.В., М: Просвещение, 1991.
4. Безруких М.М, Ефимова С.П. Знаете ли вы своего ученика, М: Просвещение, 1991.
5. Венгер Л.А Педагогика способностей. Изд-во «Знание» Москва, 1978.
6. Власова Т.А., Певзнер М.С. О детях с отклонениями в развитии. М.,1973.
7. Гельфан Е.М. Арифметические игры и упражнения. М: Просвещение, 1968.
8. Дети с задержкой психического развития. Под ред. Власовой Т.А., Певзнер М.С. М: Педагогика,1971.
9. Егорова Т.В., Лонина В.А., Розанова Т.В. Развитие наглядно-образного мышления у аномальных детей. Дефектология, 1975 №4
10. Жигалкина Т.К. Игровые и занимательные задания по математике. М: Просвещение, 1989.
11. Житомирский В.Г., Шеврин Л.Н. Геометрия для малышей. М: Педагогика,1978.
12. Истомина Н.Б. Активизация учащихся на уроках математики в начальных классах. М: Просвещение, 1985.
13. Крутецкий В.А. Психология математических способностей школьников. М: Просвещение, 1968.
14. Крутецкий В.А. Основы педагогической психологии. М: Просвещение, 1972.
15. Кумарина Г.Ф. Методика отбора детей в коррекционные классы. Методическое пособие НИИ общей педагогики АПНСССР М,1990.
16. Кумарина Г.Ф. Педагогическая диагностика учения и развития школьников в системе коррекционного обучения. Педагогическая карта учащегося. Методические рекомендации. НИИ общей педагогики АПН СССР, М.1988.
17. Кордемский Б.А. Увлечь школьников математикой. М: Просвещение, 1981.
18. Лурия А.Г. Проблемы высшей нервной деятельности нормального и аномального ребёнка. Т.ПМ.,1956.
19. Менчинская Н.А. Краткий обзор состояния проблемы неуспеваемости школьников – В кн: Психологические проблемы неуспеваемости школьников. М.,1971.
20. Минскин Е.М. От игры к знаниям. М: Просвещение, 1987.
21. Морро М.И., Бантова М.А., Бельжюкова Г.В. Математик, учебник для 1-го класса трехлетней начальной школы. М: Просвещение, 1986.
22. Моро М.И. , Бантова М.А. Математика – 2 класс (I-3) М: Просвещение.
23. Обучение в коррекционных классах. Работа со слабоуспевающими школьниками. Пособие для учителей. Под ред. Кумариной Г.Ф. М,1991.
24. Пчёлко А.С. Бантова М.А., Моро М.И., Пышкало А.М. Математика, 3 класс (1-3) М: Просвещение.
25. Цымбалюк А.Н. Особенности познавательной активности младших школьников с пониженной обучаемостью. Автореферат канд. дисс. М,1974.
Похожие работы
... его занимательным, и дети, слушая стихи, незаметно включаются в учебный процесс и приобретают новые знания. (см. приложение) 2. Методика обучения математике в специальной школе, направленных на развитие математических способностей учащихся Обучение – это прежде всего дифференцированный процесс. Обучение в каждом конкретном классе индивидуально и зависит от состава класса. Поэтому ...
... и внешне – своим открытым поведением, а внутренне – своим психическими процессами и чувствами. Выводы по первому разделу Для развития всех познавательных процессов младшего школьника необходимо соблюдать следующие условия: 1. Учебная деятельность должна быть целенаправленной, вызывать и поддерживать постоянный интерес у учащихся; 2. Расширять и развивать познавательные интересы у ...
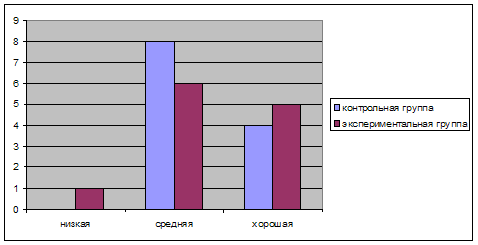
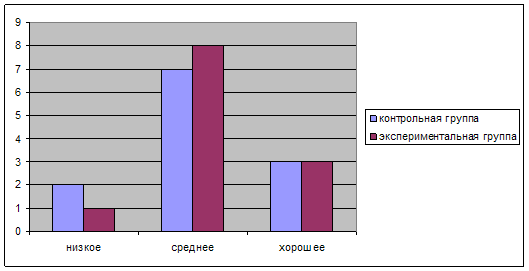
... что качественные изменения в экспериментальной группе выше, чем в контрольной. Результативность проведенной работы по развитию познавательных процессов младших школьников с использованием игр очевидна и представлена в линейных диаграммах 1 - 6. Таким образом, игра – эффективное средство развития познавательных способностей детей в младшем школьном возрасте. Диаграмма 1. ...
... ; нахождение и мотивирование выборку, соответствующей условиям проведенного исследования; организации эмпирическое исследование, относительно поставленной гипотезе; определению гендерные различия в уровне развития адаптационных способностей младших школьников к школьному обучению; построению выводов по результатам данного исследования. Для решения поставленных задач была обследована значительная ...
0 комментариев