Баллов – очень высокий уровень

10 баллов – очень высокий уровень,

4,8 – 8,0 баллов – высокий уровень,

1,5 – 3,5 баллов – средний уровень,

0,8 баллов – низкий уровень.

Из таблицы видно, что большая часть детей (5 человек) имеет средний уровень наглядно-действенного мышления, 3 человека имеет высокий уровень развития и 2 человека – низкий уровень.

Методика 2 . "Матрица Равена"

Эта методика предназначена для оценивания наглядно-образного мышления у младшего школьника. Здесь под наглядно-образным мышлением понимается такое , которое связано с оперированием различными образами и наглядными представлениями при решении задач.

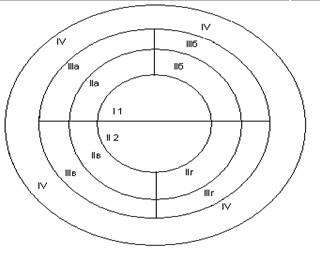
Конкретные задания, используемые для проверки уровня развития наглядно-образного мышления, в данной методике взяты из известного теста Равена. они представляют собой специальным образом подобранную выборку из 10 постепенно усложняющихся матриц Равена. (см. Приложение №1).

Ребенку предлагается серия из десяти постепенно усложняющихся задач одинакового типа: на поиск закономерностей в расположении десяти деталей на матрице и подбор одного из восьми данных ниже рисунков в качестве недостающей вставки к этой матрице, соответствующей ее рисунку. Изучив структуру большой матрицы, ребенок должен указать ту из деталей, которая лучше всего подходит к этой матрице, т. е. соответствует ее рисунку или логике расположения ее деталей по вертикали и по горизонтали.

На выполнение всех десяти заданий ребенку отводится 10 минут. По истечении этого времени эксперимент прекращается и определяется количество правильно решенных матриц, а также общая сумма баллов, набранных ребенком за их решение. Каждая правильно решенная матрица оценивается в 1 балл.

Ниже показан пример матрицы:

Результаты выполнения детьми методики представлены в следующей таблице:

№ п\п	Ф. И. учащегося	Задание										Правильно решенных задач (баллы)
		1	2	3	4	5	6	7	8	9	10
1	Кушнерев Александр	+	+	-	-	+	+	-	+	+	-	6
2	Данилина Дарья	+	-	-	-	+	+	+	+	-	-	5
3	Кирпичев Алексей	-	+	+	+	-	-	+	+	+	-	6
4	Мирошников Валерий	+	-	+	-	+	+	-	+	-	+	6
5	Еременко Марина	-	-	+	+	-	+	+	+	-	-	5
6	Сулейманов Ренат	+	+	+	+	+	-	+	+	+	-	8
7	Тихонов Денис	+	+	+	-	+	+	+	-	-	+	7
8	Черкашин Сергей	+	-	-	-	+	-	-	+	-	-	3
9	Тенизбаев Никита	+	+	+	-	+	+	+	-	+	+	8
10	Питимко Артем	-	+	-	-	-	+	+	-	-	-	3

Выводы об уровне развития:

10 баллов – очень высокий;

8 – 9 баллов – высокий;

4 – 7 баллов – средний;

2 – 3 балла – низкий;

0 – 1 балл – очень низкий.

Как видно из таблицы 2 ребенка имеют высокий уровень развития наглядно-образного мышления, 6 детей – средний уровень развития и 2 ребенка – низкий уровень развития.

Методика 3. "Лабиринт (А. Л. Венгера).

Целью данной методики является определение уровня развития наглядно-образного мышления детей младшего школьного возраста.

Ребенку нужно найти путь к определенному домику среди других, неверных, путей и тупиков лабиринта. В этом ему помогают образно заданные указания – мимо каких объектов (деревьев, кустов, цветов, грибов) он пройдет. ребенок должен ориентироваться в самом лабиринте и схеме. отражающей последовательность этапов пути. Одновременно методику "Лабиринт" целесообразно использовать в качестве упражнений для развития наглядно-образного и наглядно-действенного мышления (см. Приложение №2).

Оценка результата:

Количество баллов, получаемых ребенком, устанавливается по шкале оценок (см. Приложение №2).

После проведения методики получили следующие результаты:

2 ребенка имеют высокий уровень развития наглядно-образного мышления;

6 детей – средний уровень развития;

2 ребенка – низкий уровень развития.

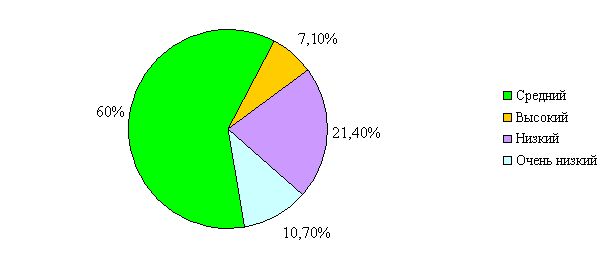
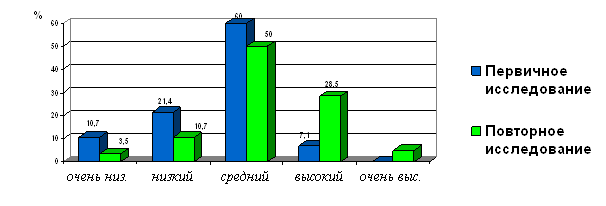
Таким образом, при проведении предварительного эксперимента группа учащихся (10 человек) показала следующие результаты:

60% детей имеет средний уровень развития наглядно-действенного и наглядно-образного мышления;

20% - высокий уровень развития и

20% - низкий уровень развития.

Результаты диагностики можно представить в виде диаграммы:

3.2. Особенности использования интегрированных уроков по математике и трудовому обучению при развитии наглядно-действенного и наглядно-образного мышления младших школьников.

 

На основе предварительного эксперимента мы определили, что у детей недостаточно развито наглядно-действенное и наглядно-образное мышления. для более высокого уровня развития этих видов мышления были проведены интегрированные уроки математики и трудового обучения. уроки проводились по программе "Математика и конструирование", авторами которой являются С. И. Волкова и О. Л. Пчелкина. (см. Приложение №3).

Приведем фрагменты уроков, которые способствовали развитию наглядно-действенного и наглядно-образного мышления.

Тема: Знакомство с треугольником. Построение треугольников. Виды треугольников.

Этот урок направлен на развитие умения анализировать, творческого воображения, наглядно-действенного и наглядно-образного мышления; научить в результате практических упражнений строить треугольник.

Фрагмент 1.

Соедините точку 1 с точкой 2, точку 2 с точкой , точку 3 с точкой 1.

-     Что это такое? – спросил Циркуль.

-     Да это же ломаная линия! – воскликнула точка.

-     А сколько в ней отрезков, ребята?

-     А углов?

-     Ну, вот это и есть треугольник.

После знакомства детей с видами треугольника (остроугольный, прямоугольный, тупоугольный) были заданы следующие задания:

1)   Обведите вершину прямого угла треугольника красным карандашом, тупого угла – синим, острого – зеленым. Закрась прямоугольный треугольник.

2)   Закрась остроугольные треугольники.

3)   Найдите и отметьте прямые углы. Посчитайте и запишите сколько прямоугольных треугольников изображено на чертеже.

Тема: Знакомство с четырехугольником. Виды четырехугольников. Построение четырехугольников.

Этот урок направлен на развитие всех видов мышления, пространственное воображение.

Приведу примеры заданий на развитие наглядно-действенного и наглядно-образного мышления.

Фрагмент 2.

I. Повторение.

а) повторение об углах.

Возьмите лист бумаги. Произвольно согните его. разверните. получили прямую линию. Теперь согните лист по-другому. Посмотрите на углы, которые получили без линейки и карандаша. Назовите их.

Согните из проволоки:

После знакомства с четырехугольником и его видами, были предложены следующие задания:

1)

Сколько квадратов?

2) Сосчитайте прямоугольники.

4)   Найдите 9 квадратов.

Фрагмент 3.

Для выполнения практической работы было предложено такое задание:

Скопируйте данный четырехугольник, вырежи его, проведи диагонали. Разрежьте четырехугольник на два треугольника по той диагонали, которая длиннее и выложи из полученных треугольников такие фигуры, как показаны ниже.

Тема: Повторение знаний о квадрате. Знакомство с игрой "Танграм", конструирование из его частей.

Этот урок направлен на активацию познавательной деятельности через решение логических задач, развитие наглядно-образного и наглядно-действенного мышления, внимания, воображения, стимулирование активного творческого труда.

Фрагмент 4.

II. Устный счет.

- Урок начнем с небольшой экскурсии в "геометрический лес".

Дети, мы с вами попали в необычный лес. Чтобы в нем не заблудиться, надо назвать геометрические фигуры, которые "спрятались" в этом лесу. Назовите геометрические фигуры, какие вы здесь видите.

Задание на повторение понятия прямоугольника.

- Найдите соответствующие пары, чтобы при их сложении получалось три прямоугольника.

На этом уроке использовалась игра "Танграм" – математический конструктор. она способствует развитию рассматриваемых нами видов мышления, творческой инициативы, смекалки (см. приложение №4).

Для составления плоскостных фигур по образу необходимо не только знание названия геометрических фигур, их свойств и отличительных признаков, но и умение представить, вообразить, что получится в результате соединения нескольких фигур, зрительно расчленить образец, представленный контуром или силуэтом, на составляющие его части.

Обучение детей игре "Танграм" проводилось в четыре этапа.

1 этап. Ознакомление детей с игрой: сообщение названия, рассматривание отдельных частей, уточнение их названия, соотношение частей по размерам, усвоение способов соединения их между собой.

2 этап. Составление сюжетных фигур по элементарному изображению предмета.

Составление предметных фигур по элементарному изображению состоит в механическом подборе, копировании способа расположения частей игры. Необходимо внимательно рассмотреть образец, назвать составные части, их расположение и соединение.