Навигация
Этап. Составление сюжетных фигур по частичному элементарному изображению
3 этап. Составление сюжетных фигур по частичному элементарному изображению.
Детям предлагаются образцы, на которых указано место расположения одной – двух составных частей, остальные они должны расположить самостоятельно.
4 этап. Составление сюжетных фигур по контурному, или силуэтному, образцу.
На этом уроке было знакомство с игрой "Танграм"
Фрагмент 5.
- Это древняя китайская игра. В целом это квадрат, разделенный на 7 частей. (показ схемы)
- Из этих частей вы должны сконструировать изображение свечи. (показ схемы)
Тема: Круг, окружность, их элементы; циркуль, его использование, построение окружности с помощью циркуля. "Волшебный круг", составление различных фигур из "волшебного круга".
Этот урок послужил развитию умения анализировать, сравнивать, логического мышления, наглядно-действенного и наглядно-образного мышления, воображения.
Примеры заданий на развитие наглядно-действенного и наглядно-образного мышления.
Фрагмент 6.
(после разъяснения и показа учителя, как начертить окружность с помощью циркуля, дети выполняют такую же работу).
- Ребята, у вас на столах лежит картон. Начертите на картоне окружность радиусом 4 см.
Затем, на листах красного цвета учащиеся чертят окружность, вырезают круги, с помощью карандаша и линейки делят круги на 4 равные части.
Одну часть отделяют от круга (заготовка для шляпки гриба).
Изготавливают ножку для гриба, склеивают все части.
Составление предметных картинок из геометрических фигур.
- В "Стране круглых фигур" жители придумали свои игры, в которых используются круги, разделенные на различные фигуры. Одна из таких игр называется "Волшебный круг". С помощь. этой игры можно выложить различных человечков из геометрических фигур, составляющих круг. А человечки эти необходимы для того, чтобы собирать грибы, изготовленные вами сегодня на уроке. У вас на столах лежат круги, разделенные линиями на фигуры. Возьмите ножницы и разрежьте круг по намеченным линиям.
Затем учащиеся выкладывают человечков.
3.3. Обработка и анализ материалов эксперимента.
После проведения интегрированных уроков по математике и трудовому обучению мы провели констатирующее исследование.
Участвовала та же группа учащихся, использовались задания предварительного эксперимента с целью выявления, на сколько процентов повысился уровень развития мышления младшего школьника после проведения интегрированных уроков математики и трудового обучения. После проведения всего эксперимента вычерчивается диаграмма, из которой можно увидеть, на сколько процентов повысился уровень развития наглядно-действенного и наглядно-образного мышления детей младшего школьного возраста. Делается соответствующий вывод.
Методика 1. "Кубик Рубика"
После проведенния этой методики были получены следующие результаты:
| № п\п | Ф. И. учащегося | Задание | Общий результат (балл) | Уровень развития наглядно-дей ст-венного мыш- ления | ||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||||
| 1 | Кушнерев Александр | + | + | + | + | + | + | + | + | - | 8 | высокий |
| 2 | Данилина Дарья | + | + | + | + | + | + | + | - | - | 6,3 | высокий |
| 3 | Кирпичев Алексей | + | + | + | + | + | - | - | - | - | 3,5 | средний |
| 4 | Мирошников Валерий | + | + | + | + | + | + | - | - | - | 4,8 | высокий |
| 5 | Еременко Марина | + | + | + | + | + | - | - | - | - | 3,5 | средний |
| 6 | Сулейманов Ренат | + | + | + | + | + | + | + | + | + | 10 | очень высокий |
| 7 | Тихонов Денис | + | + | + | + | + | + | + | - | - | 6,3 | высокий |
| 8 | Черкашин Сергей | + | + | + | - | - | - | - | - | - | 1,5 | средний |
| 9 | Тенизбаев Никита | + | + | + | + | + | + | + | + | + | 10 | очень высокий |
| 10 | Питимко Артем | + | + | + | - | - | - | - | - | - | 1,5 | средний |
Из таблицы видно, что 2 ребенка имеют очень высокий уровень развития наглядно-действенного мышления, 4 ребенка – высокий уровень развития, 4 ребенка – средний уровень развития.
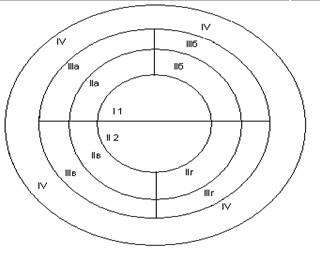
Методика 2. "Матрица Равена"
Результаты этой методики такие (см. Приложение №1):
2 человека имеют очень высокий уровень развития наглядно-образного мышления, 4 человека – высокий уровень развития, 3 человека – средний уровень развития и 1 человек – низкий уровень.
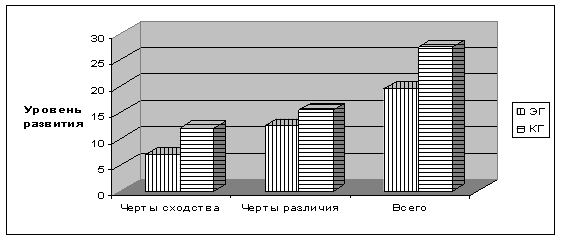
Методика 3. "Лабиринт"
После проведения методики были получены следующие результаты (см. Приложение 2):
1 ребенок – очень высокий уровень развития;
5 детей – высокий уровень развития;
3 ребенка – средний уровень развития;
1 ребенок – низкий уровень развития;
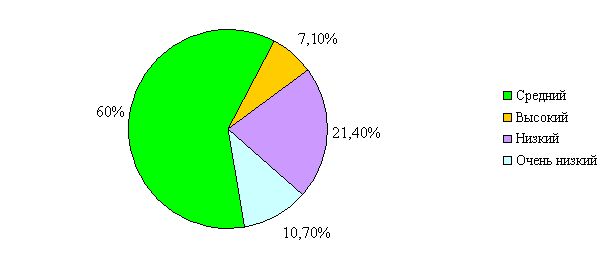
Составляя результаты диагностической работы с результатами методик, мы получили, что 60% испытуемых имеют высокий и очень высокий уровень развития, 30% - средний уровень и 10% - низкий уровень.
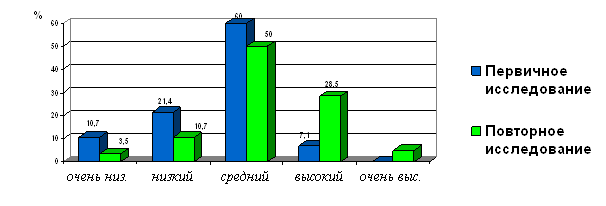
Динамика развития наглядно-действенного и наглядно-образного мышления учащихся представлена на диаграмме:
Итак, мы видим, что результаты стали намного выше, уровень развития наглядно-действенного и наглядно-образного мышления младшего школьника значительно повысился, это говорит о том, что проведенные нами интегрированные уроки математики и трудового обучения существенно улучшили процесс развития этих видов мышления второклассников, что явилось основанием доказательства правильности выдвинутой нами гипотезы.
Заключение.
Развитие наглядно-действенного и наглядно-образного мышления при проведении интегрированных уроков математики и трудового обучения, как показало наше исследование, является очень важной и актуальной проблемой.
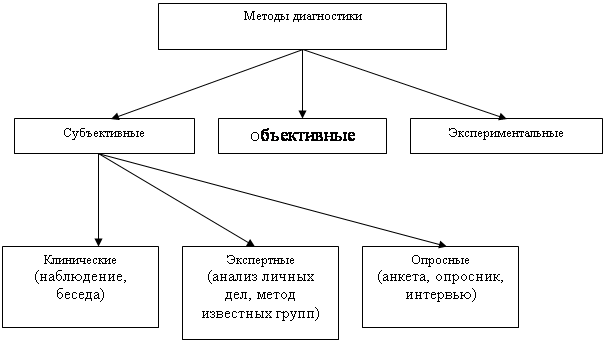
Исследуя эту проблему, мы подобрали методы диагностики наглядно-действенного и наглядно-образного мышления применительно к младшему школьному возрасту.
Для улучшения геометрических знаний и развития рассматриваемых видов мышления нами были разработаны и проведены интегрированные уроки математики и трудового обучения, на которых детям понадобились не только математические знания, но и трудовые умения и навыки.
Интеграция в начальной школе, как правило, имеет количественный характер – "немного обо всем". Это значит, что дети получают все новые и новые представления о понятиях, систематические дополняя и расширяя круг уже имеющихся знаний (двигаясь в познании по спирали). В начальной школе интеграцию целесообразно строить на объединении достаточно близких областей знаний.
В наших уроках мы попытались объединить два разноплановых по способу овладения ими учебных предмета: математику, изучение которой носит теоретический характер, и трудовое обучение, формирование умений и навыков в котором носит практический характер.
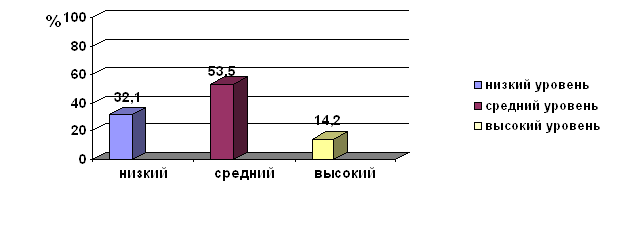
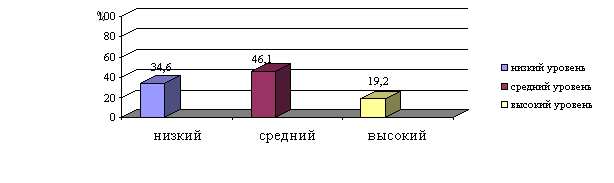
В практической части работы мы провели изучение уровня развития наглядно-действенного и наглядно-образного мышления до проведения интегрированных уроков математики и трудового обучения. Результаты первичного исследования показали, что уровень развития этих видов мышления носит слабый характер.
После проведения интегрированных уроков было проведено контрольное исследование с помощью той же диагностики. Сравнивая полученные результаты с выявленными ранее, мы установили, что эти уроки оказались эффективны для развития рассматриваемых видов мышления.
Таким образом, можно сделать вывод, что интегрированные уроки математики и трудового обучения способствуют развитию наглядно-действенного и наглядно-образного мышления.
Список использованной литературы:
| 1. | Абдулин О. А. Педагогика. М.: Просвещение, 1983. |
| 2. | Актуальные вопросы методики преподавания математики.: Сборник трудов. –М.:МГПИ, 1981 |
| 3. | Артемов А. С. Курс лекций по психологии. Харьков, 1958. |
| 4. | Бабанский Ю. К. Педагогика. М.: Просвещение, 1983. |
| 5. | Бантева М. А., Бельтюкова Г. В. Методика преподавания математики в начальных классах. – М. Просвещение, 1981 |
| 6. | Баранов С. П. Педагогика. М.: Просвещение, 1987. |
| 7. | Беломестная А. В., Кабанова Н. В. Моделирование в курсе "Математика и онст-руирование". // Н. Ш., 1990. - №9 |
| 8. | Болотина Л. Р. Развитие мышления учащихся // Начальная школа - 1994 - №11 |
| 9. | Брушлинская А. В. Психология мышления и кибернетика. М.: Просвещение, 1970. |
| 10. | Волкова С. И. Математика и конструирование // Начальная школа. - 1993 - №1. |
| 11. | Волкова С. И., Алексеенко О. Л. Изучение курса "Математика и конструирова-ние". // Н. Ш. – 1990. - №1 |
| 12. | Волкова С. И., Пчелкина О. Л. Альбом по математике и конструированию: 2 класс. М.: Просвещение, 1995. |
| 13. | Голубева Н. Д., Щеглова Т. М. Формирование геометрических представлений у первоклассников // Начальная школа. - 1996. - №3 |
| 14. | Дидактика средней школы / Под ред. М. Н. Скаткина. М.: Просвещение, 1982. |
| 15. | Житомирский В. Г., Шеврин Л .Н. Путешествие по стране Геометрии. М.:Педагогика - Пресс, 1994 |
| 16. | Зак А. З. Занимательные задачи для развития мышления // Начальная школа. 1985. №5 |
| 17. | Истомина Н. Б. Активация учащихся на уроках математики в начальных классах. – М. Просвещение, 1985. |
| 18. | Истомина Н. Б. Методика обучения математике в начальных классах. М.: Линка-пресс, 1997. |
| 19. | Коломинский Я. Л. Человек: психология. М.:1986. |
| 20. | Крутецкий В. А. Психология математических способностей школьников. М.: Просвещение, 1968. |
| 21. | Кудрякова Л. А. Изучаем геометрию // Начальная школа. - 1996. - №2. |
| 22. | Курс общей, возрастной и педагогической психологии: 2/под. Ред. М. В. Гамезо. М.: Просвещение, 1982. |
| 23. | Марцинковская Т. Д. Диагностика психического развития детей. М.: Линка-пресс, 1998. |
| 24. | Менчинская Н. А. Проблемы учения и умственного развития школьника: Избранные психологические труды. М.: Просвещение, 1985. |
| 25. | Методика начального обучения математике. /Под общ. ред. А. А. Столяра, В. Л. Дроздова – Минск: Высш. школа, 1988. |
| 26. | Моро М. И., Пышкало Л. М. Методика обучения математике в 1 – 3 кл. – М.: Просвещение, 1978. |
| 27. | Немов Р. С. Психология. М., 1995. |
| 28. | О реформе общеобразовательной профессиональной школы. |
| 29. | Пазушко Ж. И. Развивающая геометрия в начальной школе // Начальная школа. - 1999. - №1. |
| 30. | Программы обучения по системе Л. В. Занкова 1 – 3 классы. – М.: Просвещение, 1993. |
| 31. | Программы общеобразовательных учебных заведений в РФ начальных классах (1 – 4 ) – М.: Просвещение, 1992. Программы развивающего обучения. (система Д. Б. Эльковнина – В. В. Давыдова) |
| 32. | Рубинштейн С. Л. Проблемы общей психологии. М., 1973. |
| 33. | Стойлова Л. П. Математика. Учебное пособие. М.: Академия, 1998. |
| 34. | Тарабарина Т. И., Елкина Н. В. И учеба, и игра: математика. Ярославль: Академия развития, 1997. |
| 35. | Фридман Л. М. Задачи на развитие мышления. М.: Просвещение, 1963. |
| 36. | Фридман Л. М. Психологический справочник учителю М.: 1991. |
| 37. | Чилингирова Л., Спиридонова Б. Играя, учимся математике. - М.,1993. |
| 38. | Шардаков В. С. Мышление школьников. М.: Просвещение, 1963. |
| 39. | Эрдниев П. М. Обучение математике в начальных классах. М.: АО "Столетие", 1995. |
Похожие работы
... находить различные пути и способы решения часто приносит успех и удовлетворяет как частные так и глобальные интересы. Анализ школьных программ по математике дает возможность расставить основные вехи развития творческого мышления школьников, поскольку овладение таким максимально абстрактным предметом, как математика, хорошо показывает, до какого максимума поднимается мышление школьников ...
... и внешне – своим открытым поведением, а внутренне – своим психическими процессами и чувствами. Выводы по первому разделу Для развития всех познавательных процессов младшего школьника необходимо соблюдать следующие условия: 1. Учебная деятельность должна быть целенаправленной, вызывать и поддерживать постоянный интерес у учащихся; 2. Расширять и развивать познавательные интересы у ...
... всему тесту в целом, что говорит о том, что у них уровни развития мыслительных операций сравнения и обобщения выше, чем у слабоуспевающих школьников. Если анализировать индивидуальные данные по субтестам, то затруднения при ответах на отдельные вопросы говорят о слабом владении данными логическими операциями. Данные затруднения наиболее часто встречаются именно у слабоуспевающих школьников. Это ...
... младшего школьника. Объект исследования: развитие образного мышления у учащихся 2 класса средней школы №1025. Метод: тестирование. Глава 1. Теоретические основы исследования образного мышления 1.1. Понятие о мышлении Наше познание окружающей действительности начинается с ощущений и восприятия и переходит к мышлению. Функция мышления – расширение границ познания путем выхода за ...

0 комментариев