Навигация
Виберемо деякий елемент x масиву A випадковим образом;
1 Виберемо деякий елемент x масиву A випадковим образом;
2.Переглядаємо масив у прямому напрямку (i = 1, 2,...), шукаючи
в ньому елемент A[i] не менший за x;
3.Переглядаємо масив у зворотньому напрямку (j = n, n-1,..),
шукаючи в ньому елемент A[j] не більший за x;
4.Змінюємо місцями A[i] і A[j];
Пункти 2-4 повторюємо доти, поки i < j;
У результаті такого зустрічного проходу початок масиву A[1..i] і кінець масиву A[j..n] виявляються розділеними “бар'єром” x: A[k] ( x при k < i, A[k] ( x при k > j , причому на поділ ми затратимо не більш n/2 перестановок. Тепер залишилося проробити ті ж дії з початком і кінцем масиву, тобто застосувати їх рекурсивно.
Таким чином, описана нами процедура Hoare залежить від параметрів k та m - початкового і кінцевого індексів відрізка масиву, який обробляється.
Procedure Swap(i, j : Integer);
Var b : Real;
Begin
b := a[i]; a[i] := a[j]; a[j] := b
End;
Procedure Hoare(L, R : Integer);
Var left, right : Integer;
x : Integer;
Begin
If L < R then begin
x := A[(L + R) div 2]; {вибір бар'єра x}
left := L; right := R ;
Repeat {зустрічний прохід}
While A[left] < x do Inc(left); {перегляд уперед}
While A[right] > x do Dec(right); {перегляд назад}
If left <= right then begin
Swap(left, right); {перестановка}
Inc(left); Dec(right);
end
until left > right;
Hoare(L, right); {сортуємо початок}
Hoare(left, R) {сортуємо кінець}
end
End;
Program QuickSort;
Const n = 100;
Var A : array[1..n] of Integer;
{ процедури Swap, Hoare, введення і висновку }
Begin
Inp; Hoare(1, n); Out
End.
Аналіз складності алгоритму в середньому, що використовує гіпотезу про рівну імовірність усіх входів, показує, що:
C(n) = O(n log2 n), M(n) = O(n log2 n)
У гіршому випадку, коли в якості бар'єрного вибирається, наприклад, максимальний елемент підмассиву, складність алгоритму квадратична.
1.4 Метод цифрового сортуванняІноді при розв’язанні задач типу задачі сортування можна використовувати особливості типу перетворюваних даних для одержання ефективного алгоритму. Розглянемо одну з таких задач - задачу про звертання підстановки.
Підстановкою безлічі 1..n назвемо двовимірний масив A[1..2, 1..n] виду
| 1 | 2 | .......... | n-1 | n |
| J1 | j2 | ........... | jn-1 | jn |
у якому 2-ий рядок містить всі елементи відрізка 1..n. Підстановка B називається зворотньою до підстановки A, якщо B виходить з A сортуванням стовпчиків A у порядку зростання елементів 2-го рядка з наступною перестановкою рядків. Потрібно побудувати алгоритм обчислення зворотньої підстановки. З визначення випливає, що стовпчик [i, ji] підстановки A потрібно перетворити в стовпчик [ji , i] і поставити на ji-те місце в підстановці B.
{Type NumSet = 1..n;
Substitution = array[ 1..2, NumSet] of NumSet; }
Procedure Reverse ( Var A, B : Substitution);
Begin
For i := 1 to n do begin
B[A[2, i], 2] := i; B[A[2, i], 1] := A[2, i]
end
End;
Складність процедури Reverse лінійна, оскільки тіло арифметичного циклу складається з двох операторів присвоювання, в той час як стовпчики підстановки відсортовані.
2. Практична реалізація мовою Паскаль швидких алгоритмів сортування
Практичною метою нашої дослідницької роботи було написання мовою Pascal програми, яка б виконувала сортування будь-якої послідовності елементів. Для того, щоб продемонструвати роботу різних швидких алгоритмів сортування, ми залишили вибір конкретного алгоритму на розсуд користувача програми. Тобто, ми створили основну програму – меню, яка пропонує користувачеві три можливі варіанти швидких алгоритмів сортування: швидке сортування, сортування Хоара та сортування “злиттям”. Вибір певного алгоритму здійснюється за допомогою оператору “case of”, тобто натисканням клавіш клавіатури 1, 2 або 3. Також ми передбачили варіант, коли користувач програми натискає будь-яку іншу клавішу: в цьому випадку на екрані з’явиться повідомлення про помилку. Також, після проведення сортування за вибраним алгоритмом, користувач зможе продовжити роботу й випробувати інший алгоритм. Для цього потрібно натиснути клавіші клавіатури “у” або “д” або набрати слово “yes” чи “да” коли після завершення роботи одного з обраних алгоритмів сортування на екрані з’явиться запитання “Хотите ли вы продолжить работу с данной программой?”. Якщо ж користувач уже випробував усі алгоритми або за браком часу (або бажання) хоче завершити роботу з програмою, то йому достатньо буде лише натиснути на клавіатурі клавіші “n” або “н” чи набрати слова “no” або “нет” після того, як на екрані з’явиться зазначене вище запитання.
Програма виконує сортування послідовності за трьома алгоритмами сортування. Кожний окремий алгоритм представлений у вигляді окремої процедури.
Так, процедура Qsort виконує швидке сортування масиву, що вводиться. Під час роботи цього алгоритму відбувається аналіз даної послідовності одночасно у двох напрямках ( зліва-направо і зправа-наліво) . комп’ютер порівнює два елементи, що стоять поряд зліва. Якщо ці елементи стоять на своїх місцях, тобто перший з них є меншим за другий, то комп’ютер порівнює перший елемент з останнім. Якщо при порівнянні останній елемент виявиться меншим за перший, то комп’ютер виконає перестановку цих двох елементів. Такі дії будуть відбуватися до тих пір, поки індикатор, якій відповідає за ліву частину послідовності (в нашій процедурі це “i”) не перейде на праву частину, а індикатор, що відповідає за праву частину масиву (в нашій процедурі це “j”) не перейде на праву частину. Далі та ж сама процедура викликається рекурсивно. Тобто, якщо ліва частина вже відсортована, то ми викликаємо ту саму процедуру і комп’ютер виконує ті самі дії, але в параметрах процедури ми змінюємо ліву границю. Те саме відбувається, коли відсортована права частина масиву.
По суті цей алгоритм працює на основі алгоритму сортування обмінами, але цей алгоритм вважається швидким, оскільки перегляд послідовності відбувається у двох напрямках одночасно. Реалізовано ж цей алгоритм за допомогою оператору “if”, який відповідає за порівняння елементів, та пересилань.
Procedure _Qsort (var a:mas; low, hi: byte);
Var i,j:byte;
begin
if hi> low then
begin i:= low;
j:= hi;
x:= a[i];
While i< j do
if a[i+1]<=x then
begin
a[i]:= a[i+1];
a[i+1]:=x;
i:= i+1;
end
else
begin
if a[j]<=x then
begin
y:=a[j];
a[j]:=a[i+1];
a[i+1]:=y;
end;
j:=j-1
end;
-Qsort (a, low, i-1);
-Qsort (a, i+1, hi);
end;
end;
Процедура Mergesort виконує сортування двох масивів “злиттям”. Тобто, спочатку перший масив сортується за допомогою процедури Qsort і другий масив сортується за допомогою цієї ж процедури. Потім два, вже відсортованих масиви з’єднуються в один. А саме, за допомогою оператору “if” ми порівнюємо перший елемент одного і перший елемент другого масивів. Якщо один з них менший, то ми відсилаємо його в третій масив, а індикатор пересуваємо на наступний елемент і знов порівнюємо їх. Знову менший з двох елементів пересилаємо в третій масив, а індикатор пересуваємо. Також ми передбачили варіант, коли елементи, що порівнюються – однакові. Тоді в третій масив по-черзі записуються обидва елементи, а індикатори зміщуються на наступні елементи в обох масивах. Якщо один з масивів виявився меншим за кількістю елементів ніж інший, то решта елементів довшого масиву просто пересилається до третього масиву в тій самій послідовності (адже вихідні масиви вже відсортовані раніше процедурою Qsort). Таким чином, в результаті ми отримуємо третій масив з впорядкованими елементами.
Procedure Mergesort;
Var i, j, k: byte;
Begin
i:=1;
j:=1;
for k:=1 to n_c do c[k]:=0;
k:=1;
While ( i<= n_a ) or ( j<=n_b ) do
if i= n_a+1 then
begin
c[k]:=b[j];
k:=k+1;
j:= j+1;
end
else
if i= n_b+1 then
begin
c[k]:=a[i];
k:= k+1;
i:=i+1 ;
end
else
if a[i]= b[j] then
begin
c[k]:=b[j];
c[k+1]:= a[i];
k:=k+2;
i:=i+1;
j:=j+1
end
else
if a[i] > b[j] then
begin
c[k]:= b[j];
k:= k+1;
j:= j+1;
end
else
begin
c[k]:= a[i];
k:= k+1;
i:= i+1;
end
End;
Третя процедура описує алгоритм швидкого сортування Хоара. Це є удосконалений метод сортування, що базується на сортуванні обмінами. Тобто, спочатку ми обираємо деякий “бар’єр” (один з елементів масиву). Потім ми переглядаємо елементи, що стоять зліва від “бар’єра” і порівнюємо їх з ним. Коли ми знаходимо елемент, який є більшим за “бар’єр”, то ми починаємо перглядати масив з кінця, порівнюючи елементи з “бар’єром”. Якщо ми знайдемо в правій частині масиву елемент менший за “бар’єр”, то ми переставимо місцями елемент зліва (той, що більше за “бар’єр”)і елемент з права ( той, що менше) і продовжимо перегляд. Потім ми рекурсивно застосовуємо цю процедуру для того, щоб відсортувати початок і кінець масиву. Реалізуємо цей алгоритм за допомогою циклів “While” та “Repeat Until” та оператору “if”, який відповідає за порівняння.
Procedure HoareSearch ( var a:mas; L, R: Integer);
Var left, right, b, x: Integer;
Begin
if L < R then
begin
x:= a[( L+R) div 2];
left:= L;
right:= R;
Repeat
While a[ left] < x do left:= Succ(left);
While a[right] >x do right:= Pred(right);
If left >= right then
Begin
b:= a[left];
a[left]:= a[right];
a[right]:=b;
left:= Succ( left);
right:= Pred(right);
End;
Until left > right;
HoareSearch ( L, right);
HoareSearch (left, R);
end;
End;
Також у програмі представлена процедура, яка відповідає за введення масиву. Вона не винесена окремо в головну програму і користувач не побачить її на своєму екрані-меню. Він побачить лише ті три сортування, що написані у вигляді процедур.
В своїй роботі ми написали програму, що сортує масив за допомогою лише трьох алгоритмів сортування. Але можна створити процедури, які б містили алгоритми сортування деревом та пірамідального сортування. Це не вплине дуже суттєво на нашу програму. Потрібно буде лише додати ці процедури оператор “Case of” головної програми і користувач зможе обирати їх і використовувати їх так само, як і ті алгоритми, що вже були розглянуті нами в нашій дослідницькій роботі.
Висновки
Отже, ми розглянули як працюють швидкі алгоритми сортування і спробували визначити їх складність.
Застосування того чи іншого алгоритму сортування для вирішення конкретної задачі є досить складною проблемою, вирішення якої потребує не лише досконалого володіння саме цим алгоритмом, але й всебічного розглядання того чи іншого алгоритму, тобто визначення усіх його переваг і недоліків.
Звичайно, необхідність застосування саме швидких алгоритмів сортування очевидна. Адже прості алгоритми сортування не дають бажаної ефективності в роботі програми. Але завжди треба пам’ятати й про те, що кожний швидкий алгоритм сортування поряд із своїми перевагами може містити і деякі недоліки.
Так, алгоритм сортування деревом, хоча й працює однаково на всіх входах (так, що його складність в гіршому випадку співпадає зі складністю в середньому), але цей алгоритм має і досить суттєвий недолік: для нього потрібна додаткова пам’ять розміром 2n-1.
Розглядаючи такий швидкий алгоритм сортування, як пірамідальне сортування, можна зазначити, що цей алгоритм ефективніший ніж попередній, адже він сортує “на місці” , тобто він не потребує додаткових масивів. Крім того, цей алгоритм (“ з точністю до мультиплікативної константи” (4, 74)) оптимальний: його складність співпадає з нижньою оцінкою задачі, тобто за критеріями C(n) та M(n) він має складність O(n log2 n), але містить складний елемент в умові. Тобто, в умові A[left] має бути строго менше ніж x , а A[right] - строго більше за x. Якщо ж замість “строго більше” та “строго менше” поставити знаки, що позначають “більше, або дорівнює” та “менше, або дорівнює”, то індекси left і right пробіжать увесь масив і побіжать далі. Вийти з цієї ситуації можна було б шляхом ускладнення умов продовження перегляду, але це б погіршило ефективність програми.
В нашій роботі ми розглянули деякі швидкі алгоритми сортування та їх реалізацію мовою Pascal, дослідили не лише переваги таких алгоритмів, ефективність їх використання, але й визначили деякі недоліки окремих алгоритмів, що заважають вживати їх для вирішення першої ліпшої задачі сортування.
Отже, головною задачею, яку має вирішити людина, яка повинна розв’язати задачу сортування – це визначення як позитивних, так і усіх негативних характеристик різних алгоритмів сортування, передбачення кінцевого результату. До того ж , треба враховувати головне – чи , можливо, цю задачу задовольнить один з класичних простих алгоритмів сортування.
Список використаних джерел
1. Абрамов С. А., Зима Е. В. Начала программирования на языке Pascal. - М.: Наука, 1987.
2. Абрамов В. Г. Введение в язык Pascal: Учебное пособие для студентов вузов по специальности Прикладная математика. – М.: Наука, 1988.
3. Джонс Ж., Харроу К. Решение задач в системе Турбо-Паскаль/ Перевод с английского Улановой, Широкого. – М.: Финансы и статистика, 1991.
4. Зуев Е. А. Язык программирования Турбо Паскаль 6.0, 7.0. – М.: Радио и связь, 1993.
5. Культин Н. Б. Программирование в TurboPascal 7.0 и Delphi. - Санкт-петербург,1999.
6. Львов М. С., Співаковський О. В. Основи алгоритмізації та програмування. – Херсон, 1997.
7. Перминов О. Н. Программирование на языке Паскаль. – М.: Радио и связь, 1988.
8. Перминов О. Н. Язык программирования Pascal. – М.: Радио и свіязь,1989.
9. Турбо Паскаль 7.0 Издание 10-е стереотипное. – Санкт-Петербург: “Печатный Двор”, 1999.
10.Фаронов В. В. TurboPascal 7.0 . Начальный курс. – М.: “Нолидж”, 2000.
Похожие работы
... не повторяются. Простой путь – путь, в котором дуги не повторяются. Маршрут – последовательность ребер, составляющих, как и путь, цепочку. Длина пути взвешенного графа определяется как сумма весов – его дуг. Если граф не взвешен, то можно считать веса дуг равными 1. Кратчайшим путем между выделенной парой вершин хн и хк называется путь, имеющий наименьшую длину среди всех возможных путей между ...
... 6) + 1 =(509 mod 6) + 1 = 5 + 1=6; Алгоритм на графах: поиск кратчайшего пути. 3) (Y mod 5) + 1 =(509 mod 5) +1 =4 + 1 = 5; Алгоритм сортировки: сортировка-шейкер. 2 АЛГОРИТМ СОРТИРОВКИ: СОРТИРОВКА ШЕЙКЕР 2.1 Математическое описание задачи Сортировка – это перестановка элементов некоторого множества в заданном порядке при некоторой упорядочивающей функцию. Сортировка используется для ...
... , меняющую местами пару элементов; - собственно сортирующий алгоритм, который осуществляет сравнение и перестановку элементов до тех пор, сока все элементы множества не будут упорядочены. Подобными свойствами обладают и те пять алгоритмов сортировки, которые рассмотрены ниже. Они отобраны из множества алгоритмов, потому что, во-первых, наиболее часто используются, а во-вторых, потому что ...
... данных будет нести больше смысла, если его отсортировать каким‑либо образом. Часто требуется сортировать данные несколькими различными способами. Во‑вторых, многие алгоритмы сортировки являются интересными примерами программирования. Они демонстрируют важные методы, такие как частичное упорядочение, рекурсия, слияние списков и хранение двоичных деревьев в массиве. Наконец, сортировка ...
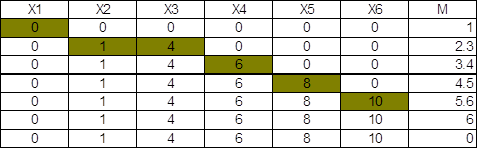
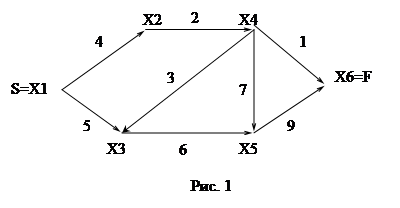
0 комментариев