Навигация
Рассмотрение процесса выполнения операции деления без восстановления в коде 8421,8421+6
1.3 Рассмотрение процесса выполнения операции деления без восстановления в коде 8421,8421+6
a) Двоично-десятичная система счисления:
Двоично-десятичный код (Д-код) десятичного числа, это такое его представление, в котором каждая десятичная цифра изображается четырьмя двоичными разрядами (тетрадой из двоичных символов):
A = {a4,n a3,n a2,n a1,n}n {a4,n-1 a3,n-1 a2,n-1 a1,n-1}n-1 ... {a4,0 a3,0 a2,0 a1,0}0 ,
где - двоичные разряды тетрады, i - номер разряда внутри тетрады, j - номер самой тетрады.
Для однозначности перевода чисел в Д-код и обратно желательно, чтобы разряды тетрад имели определенный вес. Максимальное допустимое число в тетраде - 9. Если возникает число 10 и больше, то единица переходит в следующую старшую тетраду. Существуют различные Д-коды, мы рассматрим Д-код, вес разрядов, тетрады которого следующий: 8, 4, 2, 1.
| Десятичные цифры | 8421 | 8421(+6) |
| 0 | 0000 | 0110 |
| 1 | 0001 | 0111 |
| 2 | 0010 | 1000 |
| 3 | 0011 | 1001 |
| 4 | 0100 | 1010 |
| 5 | 0101 | 1011 |
| 6 | 0110 | 1100 |
| 7 | 0111 | 1101 |
| 8 | 1000 | 1110 |
| 9 | 1001 | 1111 |
б) Свойства кода 8421
1) Коды 8421 и 8421(+6) взаимно дополняющие друг друга, и это свойство используется при выполнение алгебраического сложения.
-3 = 1.0011 пк
1.1100 ок
1
1.1101 дк = | 7 |
1.1101 № 7 (8421)
1.1101 = 7 (8421(+6))
Для рассматриваемого кода 8421нельзя получить обратный или дополнительный код простым инвертированием, т.к. инвертирование набора тетрад означает получение дополнения до .
Следовательно, необходимо убрать разницу. Один из используемых при этом приемов состоит в том, что во все цифровые тетрады числа в коде 8421 добавляется 0110 и после этого производится инвертирование набора.
Полученное изображение представляет собой обратный код числа. А дополнительный код получается, как обычно, добавлением 1 к младшему разряду младшей тетрады.
2) Аддитивность системы:
Сi = I1I2I3...In
Cj = J1J2J3...Jn
Eij = E1E2E3...En
Система счисления 8421 аддитивна
3= 0.0011
4= 0.0100
7= 0.0111
в) Алгебраическое сложение в коде 8421,8421+6
Первый случай – если слагаемые тетрады имеют одинаковые знаки
А>0, В>0, е – ?
A 0 и при этом не было переноса p = 0, то выполняется К = – 6
Если е < 0 сумма получается в коде 8421(+6), если при этом был перенос p = 1, то выполняется К = +6,
Если е < 0 сумма получается в коде 8421(+6), если при этом не было переноса p = 0, то выполняется К = 0
г) Деление в коде 8421, 8421+6
1) Тетрада рассматривается как единое целое, и сдвиг осуществляется на одну тетраду после формирования очередной тетрады частного.
2) Для формирования тетрады частного из делимого вычитают делитель до тех пор, пока знак остатка не изменится на противоположный. Если после положительного остатка получили отрицательный, то он не восстанавливается, в следующую тетраду частного записывается 9 и после сдвига начинается прибавление делителя, на каждый отрицательный остаток из текущей тетрады частного отнимается 1. При смене знака на положительный в следующую тетраду частного записывается 0 и на каждый положительный остаток в текущую тетраду частного прибавляется 1.
3) Появление остатка с противоположным знаком является признаком конца формирования очередной тетрады частного, осуществляется сдвиг остатка сразу на одну тетраду. И переходят к формированию следующей тетрады частного.
4) Каждое алгебраическое сложение требует соответствующей коррекции.
5) Пункты 2,3,4 повторяют столько раз, сколько нужно получить тетрад в частном.
Реализация примера в десятичном виде:
д.к.=9.4267
| + | 0.13570011 | 0.5733 |
| 9.4267 | 0 . 9 0 9 0 | |
| ¬ + | 9.56240011 5.62400110 | -1 +1 -1 +1 -1 +1 -1 +1 |
| 0.5733 | -1 +1 -1 +1 | |
| + | 6.19730110 | -1 -1 +1 |
| 0.5733 | -1 -1 +1 | |
| + | 6.77060110 | -1 -1 +1 |
| 0.5733 | -1 +1 | |
| + | 7.34390110 | 0 . 2 3 6 7 |
| 0.5733 | ||
| + | 7.91720110 | |
| 0.5733 | ||
| + | 8.49050110 | |
| 0.5733 | ||
| + | 9.06380110 | |
| 0.5733 | ||
| + | 9.63710110 | |
| 0.5733 | ||
| ¬ + | 0.21040110 2.10401100 | |
| 9.4267 | ||
| + | 1.53071100 | |
| 9.4267 | ||
| + | 0.95741100 | |
| 9.4267 | ||
+ | 0.38411100 | |
| 9.4267 | ||
| ¬ + | 9.81081100 8.10811000 | |
| 0.5733 | ||
| + | 8.68141000 | |
| 0.5733 | ||
| + | 9.25471000 | |
| 0.5733 | ||
| + | 9.82801000 | |
| 0.5733 | ||
| ¬ + | 0.40131000 4.01310000 | |
| 9.4267 | ||
| + | 3.43980000 | |
| 9.4267 | ||
| + | 2.86690000 | |
| 9.4267 | ||
| + | 2.29320000 | |
| 9.4267 | ||
| + | 1.71990000 | |
| 9.4267 | ||
| + | 1.14660000 | |
| 9.4267 | ||
| + | 0.57330000 | |
| 9.4267 | ||
| 0.00000000 |
Реализация примера в двоично-десятичном коде 8421, 8421+6
д.к.1111 1010 1000 1100 1101
| + | 0000 0001 0011 0101 0111 0000 0000 0001 0001 | 0110 1011 1101 1001 1001 |
| 1111 1010 1000 1100 1101 | 0000 1001 0000 1001 0000 | |
| + | 1111 1011 1100 0010 0100 | -0001+0001-0001+0001 |
| 1010 1010 1010 коррекция | -0001+0001-0001+0001 | |
| ¬ + | 1001 0101 0110 0010 0100 0000 0000 0001 0001 | -0001+0001-0001+0001 |
| 0101 0110 0010 0100 0000 0000 0001 0001 0000 | -0001 -0001+0001 | |
| 0110 1011 1101 1001 1001 | -0001 -0001+0001 | |
| + | 1100 0001 1111 1101 1001 | -0001 -0001+0001 |
| 1010 1010 1010 1010 коррекция | -0001 +0001 | |
| + | 0110 0001 1001 0111 0011 | 0010 0011 0110 0111 |
| 0110 1011 1101 1001 1001 | ||
| + | 1100 1101 0111 0000 1100 | |
| 1010 1010 1010 коррекция | ||
| + | 0110 0111 0111 0000 0110 | |
| 0110 1011 1101 1001 1001 | ||
| + | 1101 0011 0100 1001 1111 | |
| 1010 1010 1010 коррекция | ||
| + | 0111 0011 0100 0011 1001 | |
| 0110 1011 1101 1001 1001 | ||
| + | 1101 1111 0001 1101 0010 | |
| 1010 1010 1010 коррекция | ||
| + | 0111 1001 0001 0111 0010 | |
| 0110 1011 1101 1001 1001 | ||
| + | 1110 0100 1111 0000 1011 | |
| 1010 1010 1010 коррекция | ||
| + | 1000 0100 1001 0000 0101 | |
| 0110 1011 1101 1001 1001 | ||
| + | 1111 0000 0110 1001 1110 | |
| 1010 1010 1010 коррекция | ||
| + | 1001 0000 0110 0011 1000 | |
| 0110 1011 1101 1001 1001 | ||
| + | 1111 1100 0011 1101 0001 | |
| 1010 1010 1010 коррекция | ||
| + | 1001 0110 0011 0111 0001 | |
| 0110 1011 1101 1001 1001 | ||
| + | 0000 0010 0001 0000 1010 | |
| 1010 коррекция | ||
| ¬ + | 0000 0010 0001 0000 0100 0000 0001 0001 0000 0010 0001 0000 0100 0000 0001 0001 0000 0000 | |
| 1111 1010 1000 1100 1101 | ||
| + | 0001 1011 1001 0000 1101 | |
| 1010 1010 1010 коррекция | ||
| + | 0001 0101 0011 0000 0111 | |
| 1111 1010 1000 1100 1101 | ||
| + | 0000 1111 1011 1101 0100 | |
| 1010 1010 1010 коррекция | ||
| + | 0000 1001 0101 0111 0100 | |
| 1111 1010 1000 1100 1101 | ||
| + | 0000 0011 1110 0100 0001 | |
| 1010 коррекция | ||
| + | 0000 0011 1000 0100 0001 | |
| 1111 1010 1000 1100 1101 | ||
| + | 1111 1110 0001 0000 1110 | |
| 1010 1010 1010 коррекция | ||
| ¬ + | 1001 1000 0001 0000 1000 0001 0001 0000 0000 1000 0001 0000 1000 0001 0001 0000 0000 0000 | |
| 0110 1011 1101 1001 1001 | ||
| + | 1110 1100 1110 0001 1010 | |
| 1010 1010 1010 1010 коррекция | ||
| + | 1000 0110 1000 0001 0100 | |
| 0110 1011 1101 1001 1001 | ||
| + | 1111 0010 0101 0101 1101 | |
| 1010 1010 1010 коррекция | ||
| + | 1001 0010 0101 0100 0111 | |
| 0110 1011 1101 1001 1001 | ||
| + | 1111 1110 0010 1110 0000 | |
| 1010 1010 1010 коррекция | ||
| + | 1001 1000 0010 1000 0000 | |
| 0110 1011 1101 1001 1001 | ||
| + | 0000 0100 0000 0001 1001 | |
| 1010 коррекция | ||
| ¬ + | 0000 0100 0000 0001 0011 0001 0000 0000 0000 0100 0000 0001 0011 0001 0000 0000 0000 0000 | |
| 1111 1010 1000 1100 1101 | ||
| + | 0011 1010 1001 1111 1110 | |
| 1010 1010 1010 1010 коррекция | ||
| + | 0011 0100 0011 1001 1000 | |
| 1111 1010 1000 1100 1101 | ||
| + | 0010 1110 1100 0110 0101 | |
| 1010 1010 коррекция | ||
| + | 0010 1000 0110 0110 0101 | |
| 1111 1010 1000 1100 1101 | ||
| + | 0010 0010 1111 0011 0010 | |
| 1010 коррекция | ||
| + | 0010 0010 1001 0011 0010 | |
| 1111 1010 1000 1100 1101 | ||
| + | 0001 1101 0001 1111 1111 | |
| 1010 1010 1010 коррекция | ||
| + | 0001 0111 0001 1001 1001 | |
| 1111 1010 1000 1100 1101 | ||
| + | 0001 0001 1010 0110 0110 | |
| 1010 коррекция | ||
| + | 0001 0001 0100 0110 0110 | |
| 1111 1010 1000 1100 1101 | ||
| + | 0000 1011 1101 0011 0011 | |
| 1010 1010 коррекция | ||
| + | 0000 0101 0111 0011 0011 | |
| 1111 1010 1000 1100 1101 | ||
| 0000 0000 0000 0000 0000 |
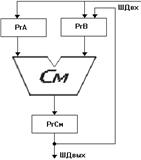
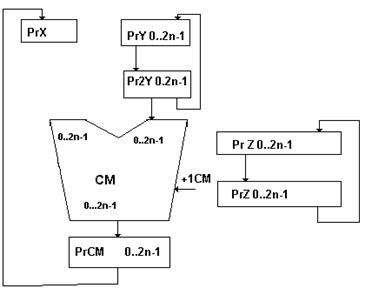
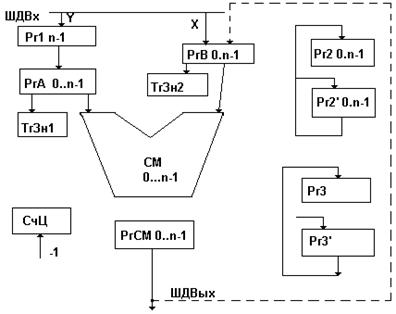
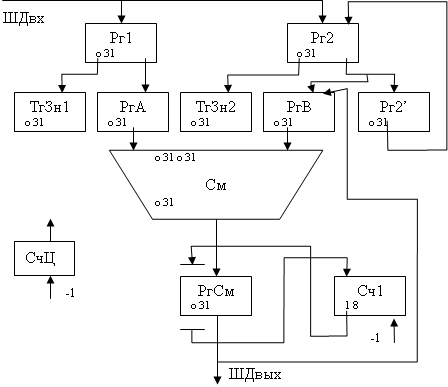
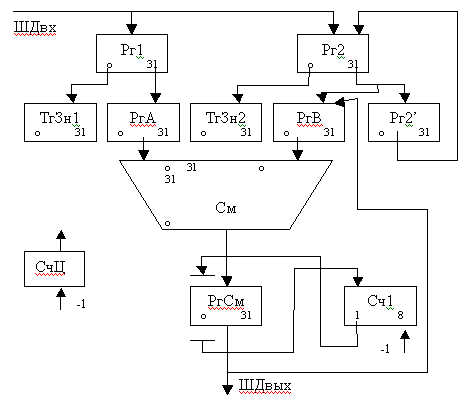
Структурная схема ОА
(Приложение А, лист № 1 )
Для реализации предложенного алгоритма выполнения операции деления необходимы следующие операционные элементы:
Рг.А(0-19) – регистр делителя: 4р.- знак, 16р.- мантисса делителя.
СМ (0-43) – сумматор: 4р.- знак, 32р.- мантисса делимого,
4р.- переносы.
3) Рг.В(0-19) – регистр частного: 4р.- знак, 16р.- мантисса частного.
4) регистр Рг.К(0-3) – регистр коррекции.
5) счетчик Сч.1 - этот счетчик необходим для формирования тетрады частного.
6) счетчик Сч.2 - этот счетчик необходим для выхода из цикла деления, выход будет осуществлен после того, как будут пройдены все тетрады.
7) счетчик Сч.3 - этот счетчик необходим для выхода из коррекции.
1.5Разработка граф-схемы алгоритма (ГСА)
(Приложение А, лист № 2,3)
Для реализации любой арифметической операции необходимо знать алгоритм ее выполнения, ниже приводится алгоритм операции деления чисел с фиксированной запятой в коде 8421, 8421+6. Если блоки выполняются последовательно, то ссылки на следующий блок не приводятся.
Таблица 1 - Определение блоков
| Номер блока | Назначение |
| A00(Л2) | Начало. |
| B00(Л2) | Начальная установка: СМ:=X, Рг.А:=Y, Сч1:=0, Сч2:=0, Сч3:=0, Рг.K:="1010". |
| C00(Л2) | Определяем знак частного путем сложения знаковых разрядов делимого и делителя по модулю два и заносим его в Рг.B[16-19]. |
| D00(Л2) | Первое пробное сложение делимого и делителя, делитель в дополнительном коде. |
| F00(Л2) | Проверяем СМ[40-43]=0000, если Да то на G00(Л2), иначе на B00(Л3). |
| G00(Л2) | Программа обработки прерываний (АВОСТ). Выдача сообщения о переполнение. |
| B00(Л3) | Проверяем СМ[22,23]=11, т.е. на наличие запрещенных комбинаций, если Да то на D00(Л3), иначе на C01(Л3). |
| C01(Л3) | Проверяем СМ[21,23]=11, т.е. на наличие запрещенных комбинаций, если Да то на D00(Л3), иначе на E00(Л3). |
| D00(Л3) | Коррекция: СМ[20-23]:=СМ[20-23] + Рг.К[0-3]. |
| E00(Л3) | Проверяем СМ[27,28]=11, т.е. на наличие запрещенных комбинаций, если Да то на G00(Л3), иначе на F01(Л3). |
| F01(Л3) | Проверяем СМ[26,28]=11, т.е. на наличие запрещенных комбинаций, если Да то на G00(Л3), иначе на B02(Л3). |
| G00(Л3) | Коррекция: СМ[25-28]:=СМ[25-28] + Рг.К[0-3]. |
| B02(Л3) | Проверяем СМ[32,33]=11, т.е. на наличие запрещенных комбинаций, если Да то на D02(Л3), иначе на C03(Л3). |
| C03(Л3) | Проверяем СМ[31,33]=11, т.е. на наличие запрещенных комбинаций, если Да то на D02(Л3), иначе на E02(Л3). |
| D02(Л3) | Коррекция: СМ[30-33]:=СМ[30-33] + Рг.К[0-3]. |
| E02(Л3) | Проверяем СМ[37,38]=11, т.е. на наличие запрещенных комбинаций, если Да то на G02(Л3), иначе на F03(Л3). |
| F03(Л3) | Проверяем СМ[36,38]=11, т.е. на наличие запрещенных комбинаций, если Да то на G02(Л3), иначе на B04(Л3). |
| G02(Л3) | Коррекция: СМ[35-38]:=СМ[35-38] + Рг.К[0-3]. |
| B04(Л3) | Проверяем СМ[42,43]=11, т.е. на наличие запрещенных комбинаций, если Да то на D04(Л3), иначе на C05(Л3). |
| C05(Л3) | Проверяем СМ[41,43]=11, т.е. на наличие запрещенных комбинаций, если Да то на D04(Л3), иначе на E04(Л3). |
| D04(Л3) | Коррекция: СМ[40-43]:=СМ[40-43] + Рг.К[0-3]. |
| E04(Л3) | Проверяем Сч.3=0, если Да, то переходим на B04(Л2), иначе на F05(Л3). |
| F05(Л3) | Проверяем Сч.3=1, если Да, то переходим на B02(Л2), иначе на B06(Л2). |
| B04(Л2) | Сдвигаем регистр СМ влево на 5 разрядов. В Сч.1 заносим 9. |
| C04(Л2) | Сч.1:=9. |
| D04(Л2) | Сложение делимого и делителя, делитель в прямом коде. |
| F04(Л2) | Сч.3:=1. |
| Переход на коррекцию. | |
| B02(Л2) | Проверяем СМ[40-43]=0000, если Да то на C02(Л2), иначе на C03(Л2). |
| C03(Л2) | Декремент Сч1 (отнимаем от текущей тетрады частного 1). |
| C02(Л2) | Инкремент Сч.2 (переход к следущей тетраде частного). Присваиваем Рг.В[0-3] значение Сч1. Сдвигаем регистр Рг.В влево на 4 разряда. |
| D02(Л2) | Сдвигаем регистр СМ влево на 5 разрядов. В Сч.1 заносим 1. |
| E02(Л2) | Сложение делимого и делителя, делитель в дополнительном коде. |
| G02(Л2) | Сч.3:=2. |
| Переход на коррекцию. | |
| B06(Л2) | Проверяем СМ[40-43]=0000, если Да то на C06(Л2), иначе на C07(Л2). |
| C06(Л2) | Инкремент Сч1 (прибавляем к текущей тетраде частного 1). |
C07(Л2) | Инкремент Сч.2 (переход к следущей тетраде частного). Присваиваем Рг.В[0-3] значение Сч1. Сдвигаем регистр Рг.В влево на 4 разряда. |
| D07(Л2) | Проверяем Сч.2=0, если Да то на E07(Л2), иначе на C04(Л2). |
| E07(Л2) | Выводим частное, т.е. Z:=Рг.В. |
| F07(Л2) | Конец. |
1.6 Описание моделирующей программы
(Приложение В)
Программа операции деления без восстановления остатка со сдвигом остатка с фиксированной точкой в коде 8421, 8421+6 выполнена на языке программирования ассемблера. В моделирующей программе регистрами Рг.А, Рг.В, Рг.К, а так же счетчиками СЧ.1 и СЧ.2 СЧ.3 являются регистры самой ЭВМ и оперативная память.
Описание программы построчно:
1 – 22 – Связывание данных с сегментом данных DS, очистка экрана, приглашение к вводу двух чисел, запись введенных чисел по адресам в сегменте данных.
23 – 28 – Вычисление знака частного.
29 – 72 – Вычисление количества тетрад, подготовка под знак целой тетрады, вызов процедур преобразования из ASCII в байты делимого и делителя, пробное сложение, проверка на переполнение.
73 – 79 – Вывод сообщения о переполнении и переход на выход из программы.
80 – 103 – Вызов процедуры преобразования конечного результата из байта в ASCII, вывод знакового разряда и вывод результата, стандартный выход из программы.
104 – 131 – Процедура перевода делимого из ASCII в BIN.
132 – 159 – Процедура перевода делимого из ASCII в BIN.
160 – 176 – Процедура перевода делителя в дополнительный код.
177 – 243 – Процедура сложения тетрад делимого и делителя с учетом возникающих межтетрадных переносов, процедура проверки на коррекцию.
244 – 267 – Процедура перевода конечного результата из байта в ASCII.
268 – 277 – Описание сегмента данных, закрытие кодового сегмента.
Оценка времени выполнения операции и оценка аппаратных затрат ОА
Время выполнения операции определяется формулой:
Топ. дел. = к*Т’Т’ = Lср.*Топ. сл.+ 4tсдв.
Топ. сл.= tсл.+tсл.*pкор.
Lср.= 5,5 – среднее количество шагов, т.к. самое минимальное значение = l, а максимальное значение = 10.
pкор=вероятность коррекции, для 8421 равна 0,5
tсл.=4*tсдв.
Т=к(L*Tсл. + 4tсдв.)=к(5,5Тсл. + 4tсдв.) = 8(5,5*1,5*4*tсдв. + 4*tсдв.)=
=8(37tсдв.)=296 tсдв.
к=8, т.к. нужно вычислить 8 тетрад.
Оценка аппаратных затрат осуществляется путем подсчета разрядов в элементах, участвующих в операции деления:
Q=Q(Рг.А(0-19))+Q(Рг.В(0-19))+Q(Рг.К(0-3))+Q(СМ(0-43))+Q(Сч.1(0-3))+Q(Сч.2(0-1))+Q(Сч.3(0-1))=20+20+4+44+4+2+2=96
Похожие работы
... этих кодов операция вычитания (или алгебраического сложения) сводится к арифметическому сложению. В результате упрощаются арифметические устройства машин. Для представления двоичных чисел в машине применяют прямой, обратный и дополнительный коды. Во всех этих кодах предусматривается дополнительный разряд для представления знака числа, причем знак «+» кодируется цифрой 0, а знак « — » - цифрой 1. ...
... схемах одинакова. Так во второй и четвертой схемах τц=τсм и, учитывая, что τсм >τсдв, эти схемы позволяют ускорить процесс выполнения операции умножения за счет совмещения операции сложения частичных произведений и сдвигов множимого; 2) по количеству оборудования предпочтение следует отдать первой, а потом третьей схеме умножения. Наиболее удобными для применения в ЭВМ ...
... 1 такт алгоритма синхронизировать выполнение сдвига на нескольких разрядах .Другим методом является работы сумматоров , а также совмещение во времени сдвиговых операций и операций суммирования Логические методы ускорения операции умножения требуют изменения центрального управления . Основным источником повышения эффективности является уменьшение кол-ва сложений выполняемых в процессе получения ...
... операции АЛУ осуществляется по шагам и результат каждого шага отражается на экране в виде кодов содержимого соответсвующего регистров, промежуточных и конечных результатов. В процессе выполнения лабораторной работы необходимо зафиксировать по шагам состояние всех элементов АЛУ, индицируемые соответствующими кодами. Работу АЛУ необходимо изучить для различных значений операндов и различных ...
0 комментариев