Навигация
3.4.1.2. Программный способ
При программном способе псевдослучайные числа нам необходимо сформировать методом умножения.
Суть метода: выбирается два n - разрядных числа X1 и X2. X1><0, X2><0. Затем X1 умножаем на X2 и получаем некоторое значение Y , у которого 2n - разрядов: Y=X1*X2. Из 2n - разрядного Y выбираем n - разрядное Х1 и Х2 и вновь полученные Х1, Х2 умножаем друг на друга. Далее все повторяется до тех пор пока не будет сформировано необходимое количество чисел.
Программа формирования ГСК на основе метода умножения приведена в Приложении № 2.
Полученные числа записываются в файл vi_gpsc1.dat и анализируются с помощью программы analize.
Определение числовых характеристик
| № | Характеристика | Теоретич. значение | Статистич. значение |
| 1 | Мин.значение совокуп. | 0.00068 | |
| 2 | Макс.значение совокуп | 0.99995 | |
| 3 | Математич. ожидание | 0.5 | 0.4928 |
| 4 | Дисперсия | 0.083 | 0.07822 |
| 5 | Сред.квад.отклонение | 0.1887 | 0.2796 |
Аппроксимация статистического распределения теоретической функцией
Проверка соответствия чисел последовательности требуемому распределению дает следующие результаты:
Критерий Хи-Квадрат:
Х2=12.9
С доверительной вероятностью 0.166 можно утверждать о согласованности теоретических и статистических данных.
Критерий Колмогорова:
Максимальная разность max| F(x)-F*(x) | = 0.0885
С доверительной вероятностью 0.999 можно утверждать о согласованности теоретических и статистических данных.
Определение характеристик корреляции
r(t)
1
0 t
5
Рис. 3. График изменения коэфф.
корреляции
Вывод:
Полученная по методу умножения последовательность СЧ, имеющих равномерный закон распределения удовлетворяет предъявленным требованиям по качеству и может быть использован в задачах моделирования, т. к.:
1) есть согласованность по критерию Колмогорова
2) числа не зависят друг от друга, о чем говорит график (Рис. 3.)
3.4.1.3. Выбор генератора РРПСЧ
Эффективность статистического моделирования и достоверность полученных результатов находятся в прямой зависимости от качества используемых в модели случайных последовательностей. Под качеством здесь понимается соответствие чисел последовательности заданной функции распределения (плотности распределения) и ее параметрам: М.О. и т.д.; независимость чисел последовательности друг от друга, т.е. отсутствие автокорреляции в последовательности случайных чисел.
Выберем генератор РРПСЧ, который используется для генерации времени между поступлениями заявок от пользователей.
Последовательность чисел, полученных аппаратным способом и хранящихся в файле vihod3.dat не совсем удовлетворяет предъявленным требованиям по качеству, т.к. нет согласия по критериям теоретических и статистических данных.
В пункте 3.4.1.2. мы делая вывод уже говорили о том, что генератор РРПСЧ сформированный программным способом (по методу умножения) можно использовать в задачах моделирования, но для простоты будем использовать встроенную функцию random( ), простую в программировании и имеющую хорошие характеристики.
3.4.2. Моделирование случайных воздействий,
имеющих неравномерное распределение
Для стохастической модели требуются числа распределенные по нормальному закону и по экспоненциальному закону.
Напишем функции формирования чисел по требуемому закону распределения. Эти числа запишем в файл. Оценим качество полученных последовательностей ПСЧ, пользуясь автоматизированной системой analize. Проанализируем результаты исследования и сделаем вывод о качестве каждой последовательности и о возможности их использования в стохастической модели.
Сведения о непрерывных случайных величинах
| Закон распределения случайных величин | Нормальный N(m,s) | Экспоненц-ый s(1,1/l)=Э(l) |
| Аналитическое выражение плотности вероятности f(x) | 1 -(x-m) f(x)=-------- e 2s sÖ2p | -lx f(x)=l e |
| Определяющие параметры | | m | < s > 0 | l > 0 |
| Числовые m характеристики D | m s | 1/l 1/l |
| Алгоритм получения случайной величины | ______ xi=Ö-2 ln z1 cos2p z2 xi+1=Ö-2 ln z1 cos2p z2 ( m=0; D=1 ) | 1 xi=- ---- ln zi l |
| Область значений случайной величины |
Исследование последовательности нормально распределенных ПСЧ.
(Программа в приложении № 3)
Определение числовых характеристик
| № |
Характеристика | Теоретическое значение | Статистическое значение |
| 1 | Мин.знач.совокупности | 11 | 12.31 |
| 2 | Макс.знач.совокуп-ти | 24 | 25.23 |
| 3 | Мат. ожидание | 16 | 16.02 |
| 4 | Дисперсия | 2 | 2.07 |
| 5 | Сред.квадр.отклонение | 1 | 1.439 |
| 6 | Коэфф.ассиметрии | 0 | 0.35 |
| 7 | Эксцесс | 0 | 2.716 |
Аппроксимация стат. распределения теоретической функцией.
Проверка соответствия чисел последовательности требуемому распределению дает следующие результаты:
Критерий Хи-Квадрат:
Х2=0.0000813
С доверительной вероятностью 0.999 можно утверждать о согласованности теоретических и статистических данных.
Критерий Колмогорова:
Максимальная разность max| F(x)-F*(x) | = 0.0823
С доверительной вероятностью 0.999 можно утверждать о согласованности теоретических и статистических данных.
Определение характеристик корреляции
r(t)
1
0 t
5
Рис. 4. График изменения коэффициента корреляции.
Вывод:
Полученная последовательность ПСЧ, имеющая нормальный закон распределения, удовлетворяет предъявленным требованиям по качеству и может быть использована в задачах моделирования, т. к.
- числовые характеристики имеют незначительное отклонение от
теоретических значений,
- по критериям согласия получены удовлетворительные значения
доверительных вероятностей,
- числа последовательности достаточно независимы, о чем свидетельствует
график (Рис. 4.)
Последовательности ПСЧ для 2-го и 3-го пользователей генерируются аналогично, с той лишь разницей, что мат. ожидание у них 17 и 18 соответственно.
Исследование последовательности экспоненциально распределенных ПСЧ
(Программа в приложении № 3)
Определение числовых характеристик
| № |
Характеристика | Теоретическое значение | Статистическое значение |
| 1 | Мин.знач.совокупности | 0.5 | 0.8 |
| 2 | Макс.знач.совокуп-ти | 3.5 | 2.358 |
| 3 | Мат. ожидание | 0.8 | 1.06 |
| 4 | Дисперсия | 0.08 | 0.066 |
| 5 | Сред.квадр.отклонение | 0.5 | 0.2575 |
| 6 | Коэфф.ассиметрии | 0 | 1.682 |
| 7 | Эксцесс | 0 | 1.097 |
Аппроксимация стат. распределения теоретической функцией
Проверка соответствия чисел последовательности требуемому закону распределения дает следующие результаты:
Критерий Хи-Квадрат:
Значение Х2=2310
С доверительной вероятностью 0.999 можно утверждать о согласованности теоретических и статистических данных.
Критерий Колмогорова:
Максимальная разность max| F(x)-F*(x) | = 0.023
С доверительной вероятностью 0.91 можно утверждать о согласованности теоретических и статистических данных.
Определение характеристик корреляции
r(t)
1
0 t
5
Рис. 5. График изменения коэффициента корреляции.
Вывод:
Полученная последовательность ПСЧ, имеющих экспоненциальный закон распределения, удовлетворяет предъявленным требованиям по качеству и может быть использована в задачах моделирования, т. к.
- числовые характеристики имеют незначительное отклонение от
теоретических значений,
- по критериям согласия получены удовлетворительные значения
доверительных вероятностей,
- числа последовательности достаточно независимы, о чем свидетельствует
график (Рис. 5.)
Похожие работы
... Математическое моделирование — метод изучения объекта исследования, основанный на создании его математической модели и использовании её для получения новых знаний, совершенствования объекта исследования или управления объектом. Математическое моделирование можно подразделить на аналитическое и компьютерное (машинное) моделирование. При аналитическом моделировании ученый — теоретик получает ...
... схема алгоритма или граф-схема алгоритма является аналогом схемы алгоритма, отличается от последней большей формализацией, несколько другим изображением блоков начала и конца. Поскольку ГСА предложена для алгоритмов операций ЭВМ, то в ней нет средств для отражения ввода-вывода. Вместо блоков в ГСА используются вершины: начальные Y0 , конечные Yк, операторные вершины Y1,Y2, … , условные вершины ...
... и вычитаются или когда значение физического типа умножается на целое. Допускается также деление на целое, но в этом случае может выполняться округление результата. Средства обеспечения параллельности в работе ВС Если говорить про операторную часть проблемно-ориентированной компоненты, то условно ее можно разделить на средства поведенческого описания аппаратуры (параллельные процессы и средства ...
... комплекса является задание на дипломную работу утвержденное приказом по академии № 07-17 от 07.02.2003 года. Наименование организации: ДГМА. Тема разработки: "Моделирование тепловых процессов при наплавке порошковой проволокой". Специальная часть: "Программно-методический комплекс для расчета температурного поля вылета порошковой проволоки". Назначение разработки Функциональное назначение ...




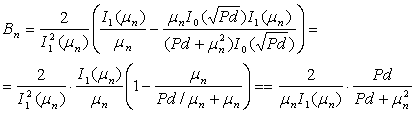


0 комментариев