Навигация
Наконец, граф можно задать посредством списков
5. Наконец, граф можно задать посредством списков.
Например:
вариант 1: списком пар вершин, соединенных ребрами (или дугами);
вариант 2: списком списков для каждой вершины множества смежных с ней вершин.
2. Задачи на графах. 2.1. Описание различных задач на графах.
Развитие теории графов в основном обязано большому числу всевозможных приложений. По-видимому, из всех математических объектов графы занимают одно из первых мест в качестве формальных моделей реальных систем.
Графы нашли применение практически во всех отраслях научных знаний: физике, биологии, химии, математике, истории, лингвистике, социальных науках, технике и т.п. Наибольшей популярностью теоретико-графовые модели используются при исследовании коммуникационных сетей, систем информатики, химических и генетических структур, электрических цепей и других систем сетевой структуры.
Далее перечислим некоторые типовые задачи теории графов и их приложения:
- Задача о кратчайшей цепи
замена оборудования
составление расписания движения транспортных средств
размещение пунктов скорой помощи
размещение телефонных станций
- Задача о максимальном потоке
анализ пропускной способности коммуникационной сети
организация движения в динамической сети
оптимальный подбор интенсивностей выполнения работ
синтез двухполюсной сети с заданной структурной надежностью
задача о распределении работ
- Задача об упаковках и покрытиях
оптимизация структуры ПЗУ
размещение диспетчерских пунктов городской транспортной сети
- Раскраска в графах
распределение памяти в ЭВМ
проектирование сетей телевизионного вещания
- Связность графов и сетей
проектирование кратчайшей коммуникационной сети
синтез структурно-надежной сети циркуляционной связи
анализ надежности стохастических сетей связи
- Изоморфизм графов и сетей
структурный синтез линейных избирательных цепей
автоматизация контроля при проектировании БИС
- Изоморфное вхождение и пересечение графов
локализация неисправности с помощью алгоритмов поиска МИПГ
покрытие схемы заданным набором типовых подсхем
- Автоморфизм графов
конструктивное перечисление структурных изомеров для
производных органических соединений
синтез тестов цифровых устройств
2.2. Нахождение кратчайших путей в графе
Начальные понятия
Будем рассматривать ориентированные графы G = <V, E>, дугам которых приписаны веса. Это означает, что каждой дуге <u, v> ÎE поставлено в соответствие некоторое вещественное число a (u, v), называемое весом данной дуги.
Нас будет интересовать нахождение кратчайшего пути между фиксированными вершинами s, t ÎV. Длину такого кратчайшего пути мы будем обозначать d (s, t) и называть расстоянием от s до t (расстояние, определенное таким образом, может быть отрицательным). Если не существует ни одного пути из s в t, то полагаем d (s, t) = ╔ . Если каждый контур нашего графа имеет положительную длину, то кратчайший путь будет всегда элементарным путем, т.е. в последовательности v1,..., vp не будет повторов.
С другой стороны, если в графе существует контур отрицательной длины, то расстояние между некоторыми парами вершин становится неопределенным, потому что, обходя этот контур достаточное число раз, мы можем показать путь между этими вершинами с длиной, меньшей произвольного вещественного числа. В таком случае, можно было бы говорить о длине кратчайшего элементарного пути, однако задача, поставленная таким образом, вероятно будет значительно более сложной, так как, в частности, она содержит в себе задачу существования гамильтонова пути.
Можно дать много практических интерпретаций задачи о кратчайших путях. Например, вершины могут соответствовать городам, а каждая дуга - некоторому пути, длина которого представлена весом дуги. Мы ищем затем кратчайшие пути между городами. Вес дуги также может соответствовать стоимости (или времени) передачи информации между вершинами. В таком случае мы ищем самый дешевый (или самый скорый) путь передачи информации. Еще одну ситуацию получаем, когда вес дуги <u, v> равен вероятности p(u, v) безаварийной работы канала передачи информации. Если предположить, что аварии каналов не зависят друг от друга, то вероятность исправности пути передачи информации равна произведению вероятностей составляющих его дуг. Задачу нахождения наиболее надежного пути легко можно свести к задаче о кратчайшем пути, заменяя веса p(u, v) на a (u, v) = - lg p(u, v).
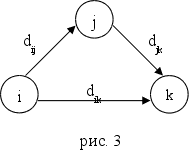
Сначала рассмотрим алгоритмы нахождения расстояния между вершинами, а не самих путей. Однако, зная расстояние, мы можем при условии положительной длины всех контуров легко определить кратчайшие пути. Для этого достаточно отметить, что для произвольных s, t Î V (s , t) существует вершина v, такая что d (s, t) = d (s, v) + a (v, t).
Действительно, таким свойством обладает предпоследняя вершина произвольного кратчайшего пути из s в t.
Далее мы можем найти вершину u, для которой d (s, v) = d (s, u) + a (u, v), и т.д.
Из положительности длины всех контуров легко следует, что созданная таким образом последовательность t, v, u, ... не сожержит повторений и оканчивается вершиной s.
Очевидно, что она определяет (при обращении очередности) кратчайший путь из s в t.
Таким образом, мы получаем следующий алгоритм:
Алгоритм нахождения кратчайшего пути
Данные: Расстояния D[v] от фиксированной вершины s до всех остальных вершин v Î V, фиксированная вершина t, матрица весов ребер, A[u, v], u, v ÎV.
Результаты: СТЕК содержит последовательность вершин, определяющую кратчайший путь из s в t.
begin
CTEK := Æ ; CTEK Ü t; v:= t;
while v ╧ s do
begin
u := вершина, для которой D[v] = D[u] + A[u, v];
CTEK Ü u;
v:= u
end
end.
Пусть <V, E> -ориентированный граф, | V| = n, | E| = m. Если выбор вершины u происходит в результате просмотра всех вершин, то сложность нашего алгоритма - O(n2). Если мы просматриваем только список ПРЕДШ[v], содержащий все вершины u, такие что u (r) v, то в этом случае сложность будет O(m).
Отметим, что в случае положительных весов ребер задача о кратчайшем пути в неориентированном графе легко сводится к аналогичной задаче для некоторого ориентированного графа. С этой целью достаточно заменить каждое ребро {u, v}двумя дугами á u, vñи áv, uñ , каждая с таким же весом, что и {u, v}. Однако в случае неположительных весов это приводит к возникновению контуров с неположительной длиной.
Далее будем всегда предполагать, что G = < V, E>является ориентированным графом, |V| = n, |E| = m. В целях упрощения изложения и избежания вырожденных случаев при оценке сложности алгоритмов будем исключать ситуации, при которых «большинство» вершин изолированные.
Будем также предполагать, что веса дуг запоминаются в массиве A[u, v], u, v Î V (A[u, v] содержит вес a (u, v)).
Кратчайшие пути от фиксированной вершины
Большинство известных алгоритмов нахождения расстояния между двумя фиксированными вершинами s и t опирается на действия, которые в общих чертах можно представить следующим образом: при данной матрице весов дуг A[u, v], u, v Î V, вычисляются некоторые верхние ограничения D[v] на расстояния от s до всех вершин v ÎV. Каждый раз, когда мы устанавливаем, что
D[u] + A[u, v] < D[v], оценку D[v] улучшаем: D[v] = D[u] + A[u, v].
Процесс прерывается, когда дальнейшее улучшение ни одного из ограничений невозможно.
Легко можно показать, что значение каждой из переменных D[v] равно тогда d (s, v) - расстоянию от s до v.
Заметим, что для того чтобы определить расстояние от s до t, мы вычисляем здесь расстояния от s до всех вершин графа.
Не известен ни один алгоритм нахождения расстояния между двумя фиксированными вершинами, который был бы существенным образом более эффективным, нежели известные алгоритмы определения расстояния от фиксированной вершины до всех остальных.
Описанная общая схема является неполной, так как она не определяет очередности, в которой выбираются вершины u и v для проверки условия минимальности расстояния. Эта очередности, как будет показано ниже, очень сильно влияет на эффективность алгоритма. Опишем теперь более детально методы нахождения расстояния от фиксированной вершины, называемой источником, его всегда будем обозначать через s, до всех остальных вершин графа.
Сначала представим алгоритм для общего случая, в котором предполагается только отсутствие контуров с отрицательной длиной. С эти алгоритмом обычно связывают имена Л.Р. Форда и Р.Е. Беллмана.
3. Программа определения кратчайшего пути в графе 3.1. Язык программирования Delphi.
Delphi - язык и среда программирования, относящаяся к классу RAD- (Rapid Application Development ‑ «Средство быстрой разработки приложений») средств CASE - технологии. Delphi сделала разработку мощных приложений Windows быстрым процессом, доставляющим вам удовольствие. Приложения Windows, для создания которых требовалось большое количество человеческих усилий например в С++, теперь могут быть написаны одним человеком, использующим Delphi.
Интерфейс Windows обеспечивает полное перенесение CASE-технологий в интегрированную систему поддержки работ по созданию прикладной системы на всех фазах жизненного цикла работы и проектирования системы.
Delphi обладает широким набором возможностей, начиная от проектировщика форм и кончая поддержкой всех форматов популярных баз данных. Среда устраняет необходимость программировать такие компоненты Windows общего назначения, как метки, пиктограммы и даже диалоговые панели. Работая в Windows , вы неоднократно видели одинаковые «объекты» во многих разнообразных приложениях. Диалоговые панели (например Choose File и Save File) являются примерами многократно используемых компонентов, встроенных непосредственно в Delphi, который позволяет приспособить эти компоненты к имеющийся задаче, чтобы они работали именно так, как требуется создаваемому приложению. Также здесь имеются предварительно определенные визуальные и не визуальные объекты, включая кнопки, объекты с данными, меню и уже построенные диалоговые панели. С помощью этих объектов можно, например, обеспечить ввод данных просто несколькими нажатиями кнопок мыши, не прибегая к программированию. Это наглядная реализация применений CASE-технологий в современном программировании приложений. Та часть, которая непосредственно связана с программированием интерфейса пользователя системой получила название визуальное программирование
Визуальное программирование как бы добавляет новое измерение при создании создании приложений, давая возможность изображать эти объекты на экране монитора до выполнения самой программы. Без визуального программирования процесс отображения требует написания фрагмента кода, создающего и настающего объект «по месту». Увидеть закодированные объекты было возможно только в ходе исполнения программы. При таком подходе достижение того, чтобы объекты выглядели и вели себя заданным образом, становится утомительным процессом, который требует неоднократных исправлений программного кода с последующей прогонкой программы и наблюдения за тем, что в итоге получилось.
Благодаря средствам визуальной разработки можно работать с объектами, держа их перед глазами и получая результаты практически сразу. Способность видеть объекты такими, какими они появляются в ходе исполнения программы, снимает необходимость проведения множества операций вручную, что характерно для работы в среде не обладающей визуальными средствами — вне зависимости от того, является она объектно-ориентированной или нет. После того, как объект помещен в форму среды визуального программирования, все его атрибуты сразу отображаются в виде кода, который соответствует объекту как единице, исполняемой в ходе работы программы.
Размещение объектов в Delphi связано с более тесными отношениями между объектами и реальным программным кодом. Объекты помещаются в вашу форму, при этом код, отвечающий объектам, автоматически записывается в исходный файл. Этот код компилируется, обеспечивая существенно более высокую производительность, чем визуальная среда, которая интерпретирует информацию лишь в ходе исполнения программы.
3.2. Программа «Определение кратчайшего пути в графе»Программа «Определение кратчайшего пути в графе» разработана в среде «Delphi», работает под ОС «Windows»-95,98,2000,NT.
Программа позволяет вводить, редактировать, сохранять графы в файл, загружать из файла. Также реализован алгоритм нахождения кратчайшего пути.
Интерфейс программы имеет следующий вид:
Верхняя панель кнопок предназначена для редактирования графа.
Кнопка «Загрузить» предназначена для загрузки ранее сохраненного графа из файла.
Кнопка «Сохранить» предназначена для сохранения графа в файл.
Кнопка «Переместить» предназначена для перемещения вершин графа.
Кнопка «Удалить» предназначена для удаления вершин графа.
При нажатии на кнопку «Новый» рабочее поле программы будет очищено и появится возможность ввода нового графа.
Кнопка «Помощь» вызывает помощь программы.
Для очистки результатов работы алгоритма определения кратчайшего пути в графе необходимо нажать кнопку «Обновить» .
При нажатии на кнопку «Настройки» на экране появится окно, в котором можно настроить параметры сетки рабочего поля программы и цвета вводимого графа.
Окно настроек выглядит следующим образом:
Нижняя панель кнопок предназначена для установки параметров ввода и запуска алгоритма определения кратчайшего пути в графе. Данная панель состоит из четырех кнопок:
При включенной кнопке «Показывать сетку» отображается сетка для удобства ввода вершин.
Для автоматического ввода длины ребра графа необходимо нажать кнопку .
При включенной кнопке «Выравнивать по сетке» новые вершины будут автоматически выравниваться по координатной сетке.
Если выбрать две различные вершины (щелчком левой кнопки мыши) и нажать на кнопку , то программа найдет кратчайший путь между вершинами.
Алгоритм определения кратчайшего пути между вершинами графа описан следующим модулем программы:
unit MinLength;
interface
uses
Windows, Messages, SysUtils, Classes, Graphics, Controls, Dialogs,
StdCtrls,IO,Data,AbstractAlgorithmUnit;
type
TMinLength = class(TAbstractAlgorithm)
private
StartPoint:integer;
EndPoint:integer;
First:Boolean;
Lymbda:array of integer;
function Proverka:Boolean;
public
procedure Make;
end;
var
MyMinLength: TMinLength;
implementation
uses MainUnit, Setting;
procedure TMinLength.Make;
var i ,j : integer;
PathPlace,TempPoint:Integer;
flag:boolean;
begin
with MyData do begin
StartPoint:=MyIO.FirstPoint;
EndPoint:=MyIO.LastPoint;
SetLength(Lymbda,Dimension+1);
SetLength(Path,Dimension+1);
for i:=1 to Dimension do
Lymbda[i]:=100000;
Lymbda[StartPoint]:=0;
repeat
for i:=1 to Dimension do
for j:=1 to Dimension do
if Matrix[i,j]=1 then
if ( ( Lymbda[j]-Lymbda[i] ) > MatrixLength[j,i] )
then Lymbda[j]:=Lymbda[i] + MatrixLength[j,i];
until Proverka ;
Path[1]:= EndPoint ;
j:=1;
PathPlace:=2;
repeat
TempPoint:=1;
Flag:=False;
repeat
if ( Matrix[ Path[ PathPlace-1 ],TempPoint] =1 )and (
Lymbda[ Path[ PathPlace-1] ] =
( Lymbda[TempPoint] + MatrixLength[ Path[PathPlace-1 ], TempPoint] ) )
then Flag:=True
else Inc( TempPoint );
until Flag;
Path[ PathPlace ]:=TempPoint;
inc( PathPlace );
MyIO.DrawPath(Path[ PathPlace-2 ],Path[ PathPlace -1],true);
// ShowMessage('f');
until(Path[ PathPlace - 1 ] = StartPoint);
// MyIO.DrawPath(Path[ PathPlace-1 ],Path[ PathPlace ],true);
end;
end;
function TMinLength.Proverka:Boolean;
var i,j:integer;
Flag:boolean;
begin
i:=1;
Flag:=False;
With MyData do begin
repeat
j:=1;
repeat
if Matrix[i,j]=1 then
if ( Lymbda[j]-Lymbda[i] )>MatrixLength[j,i]then Flag:=True;
inc(j);
until(j>Dimension)or(Flag);
inc(i);
until(i>Dimension)or(Flag);
Result:=not Flag;
end;
end;
end.
Рабочее поле программы предназначено для визуального ввода графов.
Рабочее поле с введенным графом выглядит следующим образом:
ЗАКЛЮЧЕНИЕ
Теория графов находит широкое применение в различных областях науки и техники:
Графы и информация
Двоичные деревья играют весьма важную роль в теории информации. Предположим, что определенное число сообщений требуется закодировать в виде конечных последовательностей различной длины, состоящих из нулей и единиц. Если вероятности кодовых слов заданы, то наилучшим считается код, в котором средняя длина слов минимальна по сравнению с прочими распределениями вероятности. Задачу о построении такого оптимального кода позволяет решить алгоритм Хаффмана.
Двоичные кодовые деревья допускают интерпретацию в рамках теории поиска. Каждой вершине при этом сопоставляется вопрос, ответить на который можно либо "да", либо "нет". Утвердительному и отрицательному ответу соответствуют два ребра, выходящие из вершины. "Опрос" завершается, когда удается установить то, что требовалось.
Таким образом, если кому-то понадобится взять интервью у различных людей, и ответ на очередной вопрос будет зависеть от заранее неизвестного ответа на предыдущий вопрос, то план такого интервью можно представить в виде двоичного дерева.
Графы и химия
Еще А. Кэли рассмотрел задачу о возможных структурах насыщенных (или предельных) углеводородов, молекулы которых задаются формулой:
CnH2n+2
Молекула каждого предельного углеводорода представляет собой дерево. Если удалить все атомы водорода, то оставшиеся атомы углеводорода также будут образовывать дерево, каждая вершина которого имеет степень не выше 4. Следовательно, число возможных структур предельных углеводородов, т. е. число гомологов данного вещества, равно числу деревьев с вершинами степени не больше четырех.
Таким образом, подсчет числа гомологов предельных углеводородов также приводит к задаче о перечислении деревьев определенного типа. Эту задачу и ее обобщения рассмотрел Д. Пойа.
Графы и биология
Деревья играют большую роль в биологической теории ветвящихся процессов. Для простоты мы рассмотрим только одну разновидность ветвящихся процессов – размножение бактерий. Предположим, что через определенный промежуток времени каждая бактерия либо делится на две новые, либо погибает. Тогда для потомства одной бактерии мы получим двоичное дерево.
Нас будет интересовать лишь один вопрос: в скольких случаях n-е поколение одной бактерии насчитывает ровно k потомков? Рекуррентное соотношение, обозначающее число необходимых случаев, известно в биологии под названием процесса Гальтона-Ватсона. Его можно рассматривать как частный случай многих общих формул.
Графы и физика
Еще недавно одной из наиболее сложных и утомительных задач для радиолюбителей было конструирование печатных схем.
Печатной схемой называют пластинку из какого-либо диэлектрика (изолирующего материала), на которой в виде металлических полосок вытравлены дорожки. Пересекаться дорожки могут только в определенных точках, куда устанавливаются необходимые элементы (диоды, триоды, резисторы и другие), их пересечение в других местах вызовет замыкание электрической цепи.
В ходе решения этой задачи необходимо вычертить плоский граф, с вершинами в указанных точках.
Итак, из всего вышесказанного неопровержимо следует практическая ценность теории графов.
СПИСОК ЛИТЕРАТУРЫ
1. Белов Теория Графов, Москва, «Наука»,1968.
2. Новые педагогические и информационные технологии Е.С.Полат, Москва, «Akademia» 1999 г.
3. Кузнецов О.П., Адельсон-Вельский Г.М. Дискретная математика для инженера. – М.: Энергоатомиздат, 1988.
4. Кук Д., Бейз Г. Компьютерная математика. – М.: Наука, 1990.
5. Нефедов В.Н., Осипова В.А. Курс дискретной математики. – М.: Издательство МАИ, 1992.
6. Оре О. Теория графов. – М.: Наука, 1980.
7. Исмагилов Р.С., Калинкин А.В. Матеpиалы к пpактическим занятиям по куpсу: Дискpетная математика по теме: Алгоpитмы на гpафах. - М.: МГТУ, 1995
8. Смольяков Э.Р. Введение в теоpию гpафов. М.: МГТУ, 1992
9. Hечепуpенко М.И. Алгоpитмы и пpогpаммы pешения задач на гpафах и сетях. - Hовосибиpск: Hаука, 1990
10. Романовский И.В. Алгоpитмы pешения экстpемальных задач. - М.: Hаука, 1977
11. Писсанецки С. Технология разреженных матриц. - М.: Мир, 1988
12. Севастьянов Б.А. Вероятностные модели. - М.: Наука, 1992
13. Бочаров П.П., Печинкин А.В. Теория вероятностей. - М.: Изд-во РУДН, 1994
ПРИЛОЖЕНИЕ Текст программы определения кратчайшего пути в графе
Модуль управления интерфейсом программы:
unit MainUnit;
interface
uses
Windows, Messages, SysUtils, Classes, Graphics, Controls, Forms, Dialogs,
StdCtrls,PaintingGraph, ComCtrls, ToolWin, ImgList, Menus,
ActnList, ExtCtrls;
const
crMyCursor = 5;
type
TForm1 = class(TForm)
SaveDialog1: TSaveDialog;
OpenDialog1: TOpenDialog;
ImageList1: TImageList;
ImageList2: TImageList;
LoadMenu: TPopupMenu;
ControlBar1: TControlBar;
ToolBar3: TToolBar;
OpenButton: TToolButton;
SaveButton: TToolButton;
ToolButton15: TToolButton;
ClearButton: TToolButton;
UpdateButton: TToolButton;
HelpButton: TToolButton;
ToolButton26: TToolButton;
RemovePointButton: TToolButton;
ToolButton28: TToolButton;
ToolButton32: TToolButton;
SettingButton: TToolButton;
ControlBar2: TControlBar;
AlgoritmToolBar: TToolBar;
KommiTool: TToolButton;
ToolButton: TToolButton;
NotFarButton: TToolButton;
MinLengthButton: TToolButton;
ToolButton5: TToolButton;
MovePointButton: TToolButton;
ActionList1: TActionList;
AShowGrig: TAction;
ASnapToGrid: TAction;
ASave: TAction;
ALoad: TAction;
ADelete: TAction;
GridToolBar: TToolBar;
Clock: TLabel;
Timer1: TTimer;
ShowGridButton: TToolButton;
AutoLengthButton: TToolButton;
SnapToGridButton: TToolButton;
PaintBox1: TPaintBox;
procedure FormMouseDown(Sender: TObject; Button: TMouseButton;
Shift: TShiftState; X, Y: Integer);
procedure FormCreate(Sender: TObject);
procedure FormMouseMove(Sender: TObject; Shift: TShiftState; X,
Y: Integer);
procedure FormPaint(Sender: TObject);
procedure FormKeyDown(Sender: TObject; var Key: Word;
Shift: TShiftState);
procedure ClearButtonClick(Sender: TObject);
procedure KommiToolButtonClick(Sender: TObject);
procedure PaintingToolButtonClick(Sender: TObject);
procedure SnapToGridButtonClick(Sender: TObject);
procedure HelpButtonClick(Sender: TObject);
procedure AutoLengthButtonClick(Sender: TObject);
procedure SettingButtonClick(Sender: TObject);
procedure NotFarButtonClick(Sender: TObject);
procedure MinLengthButtonClick(Sender: TObject);
procedure MovePointButtonClick(Sender: TObject);
procedure RemovePointButtonClick(Sender: TObject);
procedure Timer1Timer(Sender: TObject);
procedure ALoadExecute(Sender: TObject);
procedure AShowGrigExecute(Sender: TObject);
procedure ASaveExecute(Sender: TObject);
procedure PaintBox1Paint(Sender: TObject);
procedure UpdateButtonClick(Sender: TObject);
procedure EilerButtonClick(Sender: TObject);
procedure ClockClick(Sender: TObject);
private
procedure MyPopupHandler(Sender: TObject);
{ Private declarations }
public
{ Public declarations }
end;
var
Form1: TForm1;
implementation
uses IO,Data,Commercial,DrawingObject,Setting,NotFar,MinLength, Eiler,
SplashScreen;
{$R *.DFM}
procedure TForm1.FormMouseDown(Sender: TObject; Button: TMouseButton;
Shift: TShiftState; X, Y: Integer);
begin
if Button=mbLeft then begin
MyIO.FormMouseDown( X, Y);
if (MyIO.State=msMove)then
if MyIO.FirstPointActive then
Cursor := crMyCursor
else begin
Repaint;
Cursor := crDefault;
end;
end
else
MyIO.MakeLine(X, Y);
end;
procedure TForm1.FormCreate(Sender: TObject);
begin
Screen.Cursors[crMyCursor] := LoadCursor(HInstance, 'Shar');
MyIO:=TIO.Create(PaintBox1.Canvas);
MyData:=TData.Create;
MyDraw:=TDrawingObject.Create(PaintBox1.Canvas);
SaveDialog1.InitialDir:=ExtractFilePath(Application.ExeName)+'Grafs';
OpenDialog1.InitialDir:=ExtractFilePath(Application.ExeName)+'Grafs';
end;
procedure TForm1.FormMouseMove(Sender: TObject; Shift: TShiftState; X,
Y: Integer);
begin
MyIO.DrawLine(x,y);
end;
procedure TForm1.FormPaint(Sender: TObject);
begin
PaintBox1Paint(Sender);
end;
procedure TForm1.FormKeyDown(Sender: TObject; var Key: Word;
Shift: TShiftState);
begin
if (Key=vk_Escape) then
begin
MyData.Remove(MyData.Dimension);
MyDraw.Remove(MyData.Dimension);
Repaint;
end;
end;
procedure TForm1.MyPopupHandler(Sender: TObject);
var s:string;
begin
with Sender as TMenuItem do begin
s:=Caption;
MyData.Load(s);
System.Delete(s,length(s)-4,5);
MyDraw.Load(s+'.pos');
end;
Repaint;
end;
procedure TForm1.ClearButtonClick(Sender: TObject);
begin
MyData.Clear;
MyDraw.Clear;
Repaint;
end;
procedure TForm1.KommiToolButtonClick(Sender: TObject);
begin
If MyData.Dimension<2 then Exit;
MyCommercial:=TCommercial.Create;
MyCommercial.Make;
MyCommercial.Free;
end;
procedure TForm1.EilerButtonClick(Sender: TObject);
begin
If MyData.Dimension<2 then Exit;
EilerC:=TEiler.Create;
EilerC.Make;
EilerC.Free;
MyIO.DrawAll;
RePaint;
end;
procedure TForm1.PaintingToolButtonClick(Sender: TObject);
begin
If MyData.Dimension<2 then Exit;
MyPaint:=TPaintingGraphClass.Create;
MyPaint.Make;
RePaint;
MyPaint.Free;
end;
procedure TForm1.SnapToGridButtonClick(Sender: TObject);
begin
MyIO.FSnapToGrid:=SnapToGridButton.Down;
end;
procedure TForm1.HelpButtonClick(Sender: TObject);
begin
Application.HelpContext(10);
end;
procedure TForm1.AutoLengthButtonClick(Sender: TObject);
begin
MyIo.AutoLength:=AutoLengthButton.Down;
end;
procedure TForm1.SettingButtonClick(Sender: TObject);
begin
SettingForm.Show;
end;
procedure TForm1.NotFarButtonClick(Sender: TObject);
begin
If MyData.Dimension<2 then Exit;
MyNotFar:=TNotFar.Create;
MyNotFar.Make;
MyNotFar.Free;
end;
procedure TForm1.MinLengthButtonClick(Sender: TObject);
begin
If MyData.Dimension<2 then Exit;
MyMinLength:=TMinLength.Create;
MyMinLength.Make;
MyMinLength.Free;
end;
procedure TForm1.MovePointButtonClick(Sender: TObject);
begin
if MovePointButton.Down then MyIO.State:=msMove else
MyIO.State:=msNewPoint;
if MovePointButton.Down=false then
Cursor := crDefault;
end;
procedure TForm1.RemovePointButtonClick(Sender: TObject);
begin
if ReMovePointButton.Down then MyIO.State:=msDelete else
MyIO.State:=msNewPoint;
Repaint;
end;
procedure TForm1.Timer1Timer(Sender: TObject);
begin
Clock.Caption:=TimeToStr(Time);
end;
procedure TForm1.ALoadExecute(Sender: TObject);
var s:string;
begin
if OpenDialog1.Execute then
try
s:=OpenDialog1.Filename;
MyData.Load(s);
Delete(s,length(s)-4,5);
MyDraw.Load(s+'.pos');
finally
end;
Repaint;
end;
procedure TForm1.AShowGrigExecute(Sender: TObject);
begin
MyIO.FDrawGrid:=ShowGridButton.Down ;
Repaint;
end;
procedure TForm1.ASaveExecute(Sender: TObject);
var s:string;
m:TMenuItem;
begin
if SaveDialog1.Execute then
try
s:=SaveDialog1.Filename;
MyData.Save(s);
Delete(s,length(s)-4,5);
MyDraw.Save(s+'.Pos')
finally
end;
m:=TMenuItem.Create(Self);
m.Caption:=SaveDialog1.Filename;
m.OnClick := MyPopUpHandler;
LoadMenu.Items.Add(m);
end;
procedure TForm1.PaintBox1Paint(Sender: TObject);
begin
MyIO.DrawCoordGrid(16,16,ClientWidth-30,ClientHeight-140);
MyIO.DrawAll;
end;
procedure TForm1.UpdateButtonClick(Sender: TObject);
begin
MyDraw.SetAllUnActive;
MyIO.DrawAll;
MyIO.FirstPointActive:=false;
end;
procedure TForm1.ClockClick(Sender: TObject);
begin
Splash.Show;
end;
end.
Модуль управления окном настроек:
unit Setting;
interface
uses
Windows, Messages, SysUtils, Classes, Graphics, Controls, Forms, Dialogs,
Buttons, StdCtrls, Spin,IO,MainUnit, ExtCtrls;
type
TSettingForm = class(TForm)
GridGroupBox: TGroupBox;
Label1: TLabel;
Label2: TLabel;
ColorDialog1: TColorDialog;
Label3: TLabel;
OkBitBtn: TBitBtn;
CancelBitBtn: TBitBtn;
ColorButton: TPanel;
Label4: TLabel;
Label5: TLabel;
CoordCheckBox: TCheckBox;
GridCheckBox: TCheckBox;
StepSpinEdit: TSpinEdit;
MashtabSpinEdit: TSpinEdit;
Colors: TGroupBox;
Panel1: TPanel;
Panel2: TPanel;
Panel3: TPanel;
Label6: TLabel;
Label7: TLabel;
Label8: TLabel;
procedure ColorButtonClick(Sender: TObject);
procedure OkBitBtnClick(Sender: TObject);
procedure FormShow(Sender: TObject);
procedure FormClose(Sender: TObject; var Action: TCloseAction);
procedure CoordCheckBoxClick(Sender: TObject);
procedure GridCheckBoxClick(Sender: TObject);
procedure CancelBitBtnClick(Sender: TObject);
procedure Panel2Click(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;
var
SettingForm: TSettingForm;
implementation
{$R *.DFM}
procedure TSettingForm.ColorButtonClick(Sender: TObject);
begin
if ColorDialog1.Execute then begin
ColorButton.Color:=ColorDialog1.Color;
MyIO.GridColor:=Color;
Form1.Repaint;
end;
end;
procedure TSettingForm.OkBitBtnClick(Sender: TObject);
begin
MyIO.GridColor:=ColorButton.Color;
MyIO.GrigStep:=StepSpinEdit.Value;
MyIO.Mashtab:=MashtabSpinEdit.Value;
Close;
end;
procedure TSettingForm.FormShow(Sender: TObject);
begin
with MyIO do begin
ColorButton.Color:=MyIO.GridColor;
StepSpinEdit.Value:=MyIO.GrigStep;
MashtabSpinEdit.Value:=MyIO.Mashtab;
CoordCheckBox.Checked:=MyIO.FDrawCoord;
GridCheckBox.Checked:=MyIO.FDrawGrid;
Panel2.Color:=RebroColor ;
Panel3.Color:=TextColor ;
Panel1.Color:=MovingColor ;
end;
end;
procedure TSettingForm.FormClose(Sender: TObject;
var Action: TCloseAction);
begin
with MyIO do begin
GridColor:=ColorButton.Color;
GrigStep:=StepSpinEdit.Value;
Mashtab:=MashtabSpinEdit.Value;
FDrawCoord:=CoordCheckBox.Checked;
FDrawGrid:=GridCheckBox.Checked;
Form1.ShowGridButton.Down:=GridCheckBox.Checked;
RebroColor:=Panel2.Color ;
TextColor:=Panel3.Color ;
MovingColor:=Panel1.Color ;
end;
Form1.Repaint;
end;
procedure TSettingForm.CoordCheckBoxClick(Sender: TObject);
begin
MyIO.FDrawCoord:=CoordCheckBox.Checked;
//Form1.Repaint;
end;
procedure TSettingForm.GridCheckBoxClick(Sender: TObject);
begin
MyIO.FDrawGrid:=GridCheckBox.Checked ;
//Form1.Repaint;
end;
procedure TSettingForm.CancelBitBtnClick(Sender: TObject);
begin
Close;
end;
procedure TSettingForm.Panel2Click(Sender: TObject);
begin
with Sender as TPanel do
if ColorDialog1.Execute then begin
Color:=ColorDialog1.Color;
end;
end;
end.
Вспомогательный модуль потроения графа в окне программы:
unit IO;
interface
uses Data,DrawingObject,Graphics,windows,Math,Controls,Dialogs,SysUtils;
type
MouseState=(msNewPoint,msLining,msMove,msDelete);
TIO=class
private
xt,yt,xs,ys: integer;
// FLining: boolean;
ActivePoint: integer;
MyCanvas: TCanvas;
public
GridColor: TColor;
RebroColor: TColor;
TextColor: TColor;
MovingColor: TColor;
State: MouseState;
FDrawGrid: boolean;
FDrawCoord: boolean;
FSnapToGrid: boolean;
GrigStep: integer;
FirstPoint: integer;
FirstPointActive: boolean;
LastPoint: integer;
AutoLength: boolean;
Mashtab: integer;
procedure MakeLine(X, Y: Integer);
procedure DrawPath(First,Last:integer;Light:boolean=false);
procedure IONewPoint(xPos,yPos:integer);
procedure DrawAll;
procedure FormMouseDown( X, Y: Integer);
procedure Select(FirstPoint,LastPoint:integer);
procedure DrawCoordGrid(x,y,x1,y1:integer);
procedure DrawLine(x1,y1:Integer);
procedure RemovePoint(Num:integer);
constructor Create(Canvas:TCanvas);
end;
var MyIO:TIO;
implementation
procedure TIO.MakeLine(X, Y: Integer);
var i:integer;
V1,V2:TPoint;
begin
i:=MyDraw.FindNumberByXY(X,Y);
if i<>-1 then
if State=msLining then begin
MyData.Rebro(ActivePoint,i);
if AutoLength then begin
V1:=MyDraw.FindByNumber(ActivePoint);
V2:=MyDraw.FindByNumber(i);
MyData.SetRebroLength(ActivePoint,i,Round(
sqrt(sqr(Mashtab*(V1.x-V2.x)/ GrigStep)+
sqr(Mashtab*(V1.y-V2.y)/ GrigStep))));
end;
MyCanvas.MoveTo(xs,ys);
MyCanvas.LineTo(xt,yt);
DrawPath(ActivePoint,i,false);
State:=msNewPoint;
MyDraw.SetUnActive(ActivePoint);
end
else begin
ActivePoint:=i;
State:=msLining;
xs:=MyDraw.FindByNumber(i).x; xt:=xs;
ys:=MyDraw.FindByNumber(i).y; yt:=ys;
MyDraw.SetActive(i);
end ;
end;
procedure TIO.DrawLine(x1,y1:Integer);
begin
if State=msLining then
with MyCanvas do
begin
Pen.Width:=2;
Pen.Color:=MovingColor;
Pen.Mode:=pmXor;
Pen.Style:=psSolid;
MoveTo(xs,ys);
LineTo(xt,yt);
MoveTo(xs,ys);
LineTo(x1,y1);
xt:=x1;
yt:=y1;
end;
{if State=msMove then
with MyCanvas do
begin
Pen.Width:=2;
Pen.Color:=MovingColor;
Pen.Mode:=pmXor;
Pen.Style:=psSolid;
MoveTo(xs,ys);
LineTo(xt,yt);
MoveTo(xs,ys);
LineTo(x1,y1);
xt:=x1;
yt:=y1;
end;}
end;
procedure TIO.FormMouseDown( X, Y: Integer);
var Mini,Maxi,i,j,Temp,Te:integer;
b,k:real;
Flag:Boolean;
function StepRound(Num,Step:integer):integer;
begin
if (Num mod Step)>(Step/2)then Result:=Num- Num mod Step+Step
else Result:=(Num div Step)*Step;
end;
begin
Te:=MyDraw.FindNumberByXY(X,Y);
if (Te=-1)and(state<>msMove) then
with MyData,MyDraw do begin
i:=1;
j:=1;
Flag:=false;
repeat
repeat
if (Dimension>0)and(Matrix[i,j]=1) then begin
Mini:=Min(FindByNumber(i).x,FindByNumber(j).x);
Maxi:=Max(FindByNumber(i).x,FindByNumber(j).x);
if Mini<>Maxi then
k:=(FindByNumber(i).y-FindByNumber(j).y)/(FindByNumber(i).x-FindByNumber(j).x)
else k:=0;
b:= FindByNumber(i).y- (k*FindByNumber(i).x) ;
if (X>=Mini)and(X<Maxi) and
( Y>=(k*X+b-8) )and ( Y<=(k*X+b+8))
then begin
Flag:=true;
Select(i,j);
Exit;
end;
end;
inc(i);
until(Flag)or(i>Dimension);
inc(j);
i:=1;
until(Flag)or(j>Dimension);
end
else begin
if FirstPointActive then begin
if State=msMove then begin
flag:=true;
MyDraw.move(FirstPoint,x,y);
MyDraw.SetUnActive(FirstPoint);
DrawAll;
FirstPointActive:=False;
end;
LastPoint:=Te
end
else begin
FirstPoint:=Te;
FirstPointActive:=True;
end;
MyDraw.SetActive(Te);
if State=msDelete then
RemovePoint(Te);
Exit;
end;
if not flag then begin
if FSnapToGrid then IONewPoint(StepRound(x,GrigStep),StepRound(y,GrigStep))
else IONewPoint(x,y);end;
end;
procedure TIO.Select(FirstPoint,LastPoint:integer);
var s:string;
begin
with MyData do begin
DrawPath(FirstPoint,LastPoint,true);
S:=InputBox('Ввод','Введите длину ребра ','');
if(s='')or(not(StrToInt(S) in [1..250]))then begin
ShowMessage('Некорректно введена длина');
exit;
end;
{ if Oriented then
if Matrix[FirstPoint,LastPoint]<>0 then
MatrixLength[FirstPoint,LastPoint]:=StrToInt(S)else
MatrixLength[LastPoint,FirstPoint]:=StrToInt(S)
else
begin }
LengthActive:=True;
SetRebroLength(FirstPoint,LastPoint,StrToInt(S));
// end;
DrawPath(FirstPoint,LastPoint,false);
end;
end;
procedure TIO.DrawPath(First,Last:integer;Light:boolean=false);
var s:string;
begin
with MyDraw,MyCanvas do
begin
{!!pmMerge} Pen.Mode:=pmCopy;
Pen.Width:=2;
brush.Style:=bsClear;
Font.Color:=TextColor;
PenPos:=FindByNumber(First);
if Light then begin
Pen.Color:=clYellow;
SetActive(First);
SetActive(Last);
end
else Pen.Color:=RebroColor;
LineTo(FindByNumber(Last).x,
FindByNumber(Last).y );
if (MyData.LengthActive)and
(MyData.MatrixLength[First,Last]<>0) then
begin
s:=IntToStr(MyData.MatrixLength[First,Last]);
TextOut((FindByNumber(Last).x+FindByNumber(First).x)div 2,
(FindByNumber(Last).y+FindByNumber(First).y) div 2-13,s);
end;
DrawSelf(First);
DrawSelf(Last);
end;
end;
procedure TIO.DrawAll;
var i,j:byte;
begin
for i:=1 to MyData.Dimension do
for j:=1 to MyData.Dimension do
if MyData.Matrix[i,j]=1 then DrawPath(i,j,false);
MyDraw.DrawAll;
end;
procedure TIO.IONewPoint(xPos,yPos:integer);
begin
MyData.NewPoint;
MyDraw.NewPoint(xPos,yPos);
MyDraw.DrawAll;
end;
procedure TIO.DrawCoordGrid(x,y,x1,y1:integer);
var i,j,nx,ny,nx1,ny1:integer;
begin
if FDrawGrid then begin
nx:=x div GrigStep;
nx1:=x1 div GrigStep;
ny:=y div GrigStep;
ny1:=y1 div GrigStep;
MyCanvas.Brush.Style:=bsClear;
MyCanvas.Pen.Color:=GridColor;
for i:=1 to nx1-nx do
for j:=1 to ny1-ny do
MyCanvas.Pixels[i*GrigStep,y1-j*GrigStep]:=GridColor;
end;
if FDrawCoord then
with MyCanvas do begin
Pen.Width:=1;
MoveTo(nx+GrigStep,y-5);
LineTo(nx+GrigStep,y1+2);
LineTo(x1-4,y1+2);
{horizontal}
for i:=1 to nx1-nx do begin
MoveTo(nx+i*GrigStep,y1-1);
LineTo(nx+i*GrigStep,y1+5);
TextOut(nx+i*GrigStep-5,y1+8,IntToStr((i-1)*Mashtab));
end; {vertical}
for i:=1 to ny1-ny do begin
MoveTo(x+2,y1-GrigStep*i);
LineTo(x+7,y1-GrigStep*i);
TextOut(x-15,y1-i*GrigStep-GrigStep div 2,IntToStr(i*Mashtab));
end;
end;
end;
constructor TIO.Create(Canvas:TCanvas);
begin
GrigStep:=20;
FSnapToGrid:=true;
GridColor:=clBlack;
RebroColor:=clMaroon;
MovingColor:=clBlue;
TextColor:=clBlack;
Mashtab:=1;
MyCanvas:=Canvas;
State:=msNewPoint;
FDrawCoord:=false;
end;
procedure TIO.RemovePoint(Num: integer);
var j:integer;N,MPenPos:TPoint;
begin
{with MyCanvas do begin
Pen.Width:=2;
Pen.Color:=RebroColor;
Pen.Mode:=pmXor;
Pen.Style:=psSolid;
MPenPos:=MyDraw.FindByNumber(Num);
for j:=1 to MyData.Dimension do
if MyData.Matrix[Num,j]=1 then begin
N:=MyDraw.FindByNumber(j);
PolyLine([MPenPos,N]);
end;}
{ Pen.Mode:=pmNot;
for j:=1 to MyData.Dimension do
if MyData.Matrix[Num,j]=1 then begin
N:=MyDraw.FindByNumber(j);
PolyLine([MPenPos,N]);
end;
end;}
MyData.Remove(Num);
MyDraw.Remove(Num);
end;
end.
Модуль визуального отображения графа в окне программы:
unit DrawingObject;
interface
uses
Classes, Windows, Graphics,dialogs,SysUtils;
type
Colors=(Red,RedLight,Blue,Yellow,Green,Purple);
Obj=record
Place :TRect;
PlaceX,PlaceY :integer;
Color :Colors ;
end;
TDrawingObject = class(TObject)
protected
MyCanvas:TCanvas;
public
Dim:integer;
Bitmaps:array[1..6]of TBitmap;
Arr:array of Obj;
constructor Create(Canvas:TCanvas);
procedure Remove(Num:integer);
procedure NewPoint(x,y:integer);
procedure DrawSelf(Num:integer);
procedure DrawSelfXY(X,Y:integer);
function HasPoint(Num,X,Y:integer): Boolean;
destructor Destroy ;
procedure DrawAll;
procedure Clear;
procedure Save(FileName:string);
procedure Load(FileName:string);
procedure SetActive(Num:integer);
procedure SetUnActive(Num:integer);
procedure SetAllUnActive;
procedure Move(number,x,y:integer);
procedure SetColor(Num:integer;NewColor:byte);
function FindByNumber(Num:integer): TPoint;
function FindNumberByXY(X,Y:integer):integer ;
end;
var MyDraw:TDrawingObject;
implementation
procedure TDrawingObject.Clear;
begin
Dim:=0;
Arr:=nil;
end;
procedure TDrawingObject.NewPoint(x,y:integer);
begin
inc(Dim);
SetLength(Arr,Dim+1);
with Arr[Dim] do
begin
PlaceX:=x;
PlaceY:=y;
Place.Left:=x-Bitmaps[1].Width div 2;
Place.Top:=y-Bitmaps[1].Width div 2;
Place.Right:=x+Bitmaps[1].Width div 2;
Place.Bottom:=y+Bitmaps[1].Width div 2;
Color :=Red;
end;
end;
constructor TDrawingObject.Create(Canvas:TCanvas);
var i:byte;
begin
MyCanvas:=Canvas;
Dim:=0;
for i:=1 to 6 do
Bitmaps[i]:=TBitmap.Create;
Bitmaps[1].LoadFromResourceName(hInstance,'nBit');
Bitmaps[2].LoadFromResourceName(hInstance,'aBit');
Bitmaps[3].LoadFromResourceName(hInstance,'Blue');
Bitmaps[4].LoadFromResourceName(hInstance,'Yellow');
Bitmaps[5].LoadFromResourceName(hInstance,'Green');
Bitmaps[6].LoadFromResourceName(hInstance,'Purple');
for i:=1 to 6 do
Bitmaps[i].Transparent:=True;
end;
procedure TDrawingObject.DrawSelfXY(X,Y:integer);
begin
DrawSelf(FindNumberByXY(X,Y));
end;
procedure TDrawingObject.DrawSelf(Num:integer);
begin
with Arr[Num] do
case Color of
Red: MyCanvas.Draw(Place.Left,Place.Top,Bitmaps[1]);
RedLight: MyCanvas.Draw(Place.Left,Place.Top,Bitmaps[2]);
Blue: MyCanvas.Draw(Place.Left,Place.Top,Bitmaps[3]);
Green: MyCanvas.Draw(Place.Left,Place.Top,Bitmaps[4]);
Yellow: MyCanvas.Draw(Place.Left,Place.Top,Bitmaps[5]);
Purple: MyCanvas.Draw(Place.Left,Place.Top,Bitmaps[6]);
else
MyCanvas.Draw(Place.Left,Place.Top,Bitmaps[1]);
end;
end;
function TDrawingObject.HasPoint(Num,X,Y:integer): Boolean;
begin
with Arr[Num] do
if(X >= Place.Left) and (X <= Place.Right)
and (Y >= Place.Top) and (Y <= Place.Bottom)then
Result := True
else
Result := False;
end;
procedure TDrawingObject.DrawAll;
var
i: Integer;
begin
for i :=1 to Dim do
DrawSelf(i);
end;
function TDrawingObject.FindByNumber(Num:integer): TPoint;
begin
Result.x := Arr[Num].PlaceX;
Result.y := Arr[Num].PlaceY;
end;
function TDrawingObject.FindNumberByXY(X,Y:integer):integer ;
var
i: Integer;
begin
Result:=-1;
for i :=1 to Dim do
if HasPoint(i,X,Y) then
begin
Result:=i;
Exit;
end;
end;
procedure TDrawingObject.SetUnActive(Num:integer);
begin
Arr[Num].Color:=Red;
DrawSelf(Num);
end;
destructor TDrawingObject.Destroy ;
var i:byte;
begin
for i:=1 to 6 do
Bitmaps[i].Free;
end;
procedure TDrawingObject.Save(FileName:string);
var stream: TWriter;
st:TFileStream;
i:integer;
begin
try
st:=TFileStream.Create(FileName,fmCreate);
stream := TWriter.Create(st,256);
stream.WriteInteger(Dim);
for i:=1 to Dim do
begin
stream.WriteBoolean(true);
stream.WriteInteger(Arr[i].Place.Left);
stream.WriteInteger(Arr[i].Place.Top);
stream.WriteInteger(Arr[i].Place.Right);
stream.WriteInteger(Arr[i].Place.Bottom);
stream.WriteInteger(Arr[i].PlaceX);
stream.WriteInteger(Arr[i].PlaceY);
end;
finally
stream.Free;
st.Free;
end;
end;
procedure TDrawingObject.Load(FileName:string);
var stream: TReader;
i:integer;
st:TFileStream;
s:boolean;
begin
try
st:=TFileStream.Create(FileName,fmOpenRead);
stream := TReader.Create(st,256);
Dim:=stream.ReadInteger;
SetLength(Arr,Dim+1);
for i:=1 to Dim do
begin
Arr[i].Color:=Red;
s:=stream.ReadBoolean;
Arr[i].Place.Left:=stream.ReadInteger;
Arr[i].Place.Top:=stream.ReadInteger;
Arr[i].Place.Right:=stream.ReadInteger;
Arr[i].Place.Bottom:=stream.ReadInteger;
Arr[i].PlaceX:=stream.ReadInteger;
Arr[i].PlaceY:=stream.ReadInteger;
end;
finally
stream.Free;
st.Free;
end;
end;
procedure TDrawingObject.Remove(Num:integer);
var i:integer;
begin
for i:=Num to Dim-1 do
Arr[i]:=Arr[i+1];
Dec(Dim);
SetLength(Arr,Dim+1);
DrawAll;
end;
procedure TDrawingObject.SetActive(Num:integer);
begin
Arr[Num].Color:=RedLight;
DrawSelf(Num);
end;
procedure TDrawingObject.SetAllUnActive;
var i:byte;
begin
for i:=1 to Dim do
Arr[i].Color:=Red;
end;
procedure TDrawingObject.SetColor(Num:integer;NewColor:Byte);
begin
case NewColor of
1: Arr[Num].Color:=Red;
2: Arr[Num].Color:=RedLight;
3: Arr[Num].Color:=Blue;
4: Arr[Num].Color:=Green;
5: Arr[Num].Color:=Yellow;
6: Arr[Num].Color:=Purple;
end;
DrawSelf(Num);
end;
{$R bitmaps\shar.res}
procedure TDrawingObject.Move(number, x, y:integer);
begin
with Arr[number] do
begin
PlaceX:=x;
PlaceY:=y;
Place.Left:=x-Bitmaps[1].Width div 2;
Place.Top:=y-Bitmaps[1].Width div 2;
Place.Right:=x+Bitmaps[1].Width div 2;
Place.Bottom:=y+Bitmaps[1].Width div 2;
//Color :=Red;
end;
DrawSelf(number);
end;
end.
Модуль организации и управления данными о графе в память компьютера:
unit Data;
interface
uses Dialogs,Classes,SysUtils;
type TData=class
public
LengthActive:boolean;
Dimension: integer;
Oriented:boolean;
Matrix: array of array of Integer;
MatrixLength: array of array of Integer;
procedure Clear;
procedure NewPoint;
procedure Rebro(First,Second:integer);
procedure SetRebroLength(First,Second,Length:integer);
procedure Save(FileName:string);
procedure Load(FileName:string);
procedure Remove(Num:integer);
constructor Create;
end;
var MyData:TData;
implementation
constructor TData.Create;
begin Clear;
end;
procedure TData.Clear;
begin Oriented:=false;
LengthActive:=True;
Matrix:=nil;
MatrixLength:=nil;
Dimension:=0;
end;
procedure TData.NewPoint;
begin
inc(Dimension);
SetLength(Matrix,Dimension+1,Dimension+1);
if LengthActive then
SetLength(MatrixLength,Dimension+1,Dimension+1);
end;
procedure TData.Rebro(First,Second:integer);
begin
Matrix[First,Second]:=1;
Matrix[Second,First]:=1;
end;
procedure TData.Save(FileName:string);
var stream: TWriter;
st:TFileStream;
i,j:integer;
begin
try
st:=TFileStream.Create(FileName,fmCreate);
stream := TWriter.Create(st,256);
stream.WriteInteger(Dimension);
stream.WriteBoolean(LengthActive);
stream.WriteBoolean(Oriented);
for i:=1 to Dimension do
for j:=1 to Dimension do
stream.WriteInteger(Matrix[i,j]);
for i:=1 to Dimension do
for j:=1 to Dimension do
stream.WriteInteger(MatrixLength[i,j]);
finally
stream.Free;
st.Free;
end;
end;
procedure TData.Load(FileName:string);
var stream: TReader;
i,j:integer;
st:TFileStream;
begin
try
st:=TFileStream.Create(FileName,fmOpenRead);
stream := TReader.Create(st,256);
Dimension:=stream.ReadInteger;
SetLength(Matrix,Dimension+1,Dimension+1);
SetLength(MatrixLength,Dimension+1,Dimension+1);
LengthActive:=stream.ReadBoolean;
Oriented:=stream.ReadBoolean;
for i:=1 to Dimension do
for j:=1 to Dimension do
Matrix[i,j]:=stream.ReadInteger;
for i:=1 to Dimension do
for j:=1 to Dimension do
MatrixLength[i,j]:=stream.ReadInteger;
finally
stream.Free;
st.Free;
end;
end;
procedure TData.Remove(Num:integer);
var i,j:integer;
begin
for i:=Num to Dimension-1 do
for j:=1 to Dimension do
begin
Matrix[j,i]:=Matrix[j,i+1];
MatrixLength[j,i]:=MatrixLength[j,i+1];
end;
for i:=Num to Dimension-1 do
for j:=1 to Dimension-1 do
begin
Matrix[i,j]:=Matrix[i+1,j];
MatrixLength[i,j]:=MatrixLength[i+1,j];
end;
Dec(Dimension);
SetLength(Matrix,Dimension+1,Dimension+1);
SetLength(MatrixLength,Dimension+1,Dimension+1);
end;
procedure TData.SetRebroLength(First,Second,Length:integer);
begin
MatrixLength[First,Second]:=Length ;
MatrixLength[Second,First]:=Length ;
end;
end.
Модуль определения кратчайшего пути в графе:
unit MinLength;
interface
uses
Windows, Messages, SysUtils, Classes, Graphics, Controls, Dialogs,
StdCtrls,IO,Data,AbstractAlgorithmUnit;
type
TMinLength = class(TAbstractAlgorithm)
private
StartPoint:integer;
EndPoint:integer;
First:Boolean;
Lymbda:array of integer;
function Proverka:Boolean;
public
procedure Make;
end;
var
MyMinLength: TMinLength;
implementation
uses MainUnit, Setting;
procedure TMinLength.Make;
var i ,j : integer;
PathPlace,TempPoint:Integer;
flag:boolean;
begin
with MyData do begin
StartPoint:=MyIO.FirstPoint;
EndPoint:=MyIO.LastPoint;
SetLength(Lymbda,Dimension+1);
SetLength(Path,Dimension+1);
for i:=1 to Dimension do
Lymbda[i]:=100000;
Lymbda[StartPoint]:=0;
repeat
for i:=1 to Dimension do
for j:=1 to Dimension do
if Matrix[i,j]=1 then
if ( ( Lymbda[j]-Lymbda[i] ) > MatrixLength[j,i] )
then Lymbda[j]:=Lymbda[i] + MatrixLength[j,i];
until Proverka ;
Path[1]:= EndPoint ;
j:=1;
PathPlace:=2;
repeat
TempPoint:=1;
Flag:=False;
repeat
if ( Matrix[ Path[ PathPlace-1 ],TempPoint] =1 )and (
Lymbda[ Path[ PathPlace-1] ] =
( Lymbda[TempPoint] + MatrixLength[ Path[PathPlace-1 ], TempPoint] ) )
then Flag:=True
else Inc( TempPoint );
until Flag;
Path[ PathPlace ]:=TempPoint;
inc( PathPlace );
MyIO.DrawPath(Path[ PathPlace-2 ],Path[ PathPlace -1],true);
// ShowMessage('f');
until(Path[ PathPlace - 1 ] = StartPoint);
// MyIO.DrawPath(Path[ PathPlace-1 ],Path[ PathPlace ],true);
end;
end;
function TMinLength.Proverka:Boolean;
var i,j:integer;
Flag:boolean;
begin
i:=1;
Flag:=False;
With MyData do begin
repeat
j:=1;
repeat
if Matrix[i,j]=1 then
if ( Lymbda[j]-Lymbda[i] )>MatrixLength[j,i]then Flag:=True;
inc(j);
until(j>Dimension)or(Flag);
inc(i);
until(i>Dimension)or(Flag);
Result:=not Flag;
end;
end;
end.
Похожие работы
... этих точек. Сетевые модели используются для решения следующих задач: проектирование газопровода; нахождение кратчайшего маршрута между городами по сети дорог; определение максимальной пропускной способности при транспортировки нефти; составление временных графиков работ и др. Существуют три наиболее эффективных алгоритма нахождения кратчайшего пути: 1) алгоритм построения минимального ...
... , а также отображение найденного кратчайшего пути в лабиринте, и в случае сохранения - файл. ПРИЛОЖЕНИЕ Б (справочное) Описание применения Назначение программы Программа “Поиск кратчайшего пути” находит кратчайший путь в лабиринте. Условия применения Необходимы следующие технические средства: 1) 486 DX4 100 процессор и выше; 8 Мбайта ОЗУ и выше; Монитор, Клавиатура. ...
... 6) + 1 =(509 mod 6) + 1 = 5 + 1=6; Алгоритм на графах: поиск кратчайшего пути. 3) (Y mod 5) + 1 =(509 mod 5) +1 =4 + 1 = 5; Алгоритм сортировки: сортировка-шейкер. 2 АЛГОРИТМ СОРТИРОВКИ: СОРТИРОВКА ШЕЙКЕР 2.1 Математическое описание задачи Сортировка – это перестановка элементов некоторого множества в заданном порядке при некоторой упорядочивающей функцию. Сортировка используется для ...
... одинаково ли они понимают задачу. Диалог может длиться день, месяц… В моей ситуации требуется написать программу, чтобы она могла найти кратчайший путь передвижения короля по заданному клеточному полю, соединяющих два заданных поля доски. Причём начальная и целевая клетки указываются при помощи мыши в запущенной программе. Формальная постановка задачи Разработка или поиск алгоритма решения ...




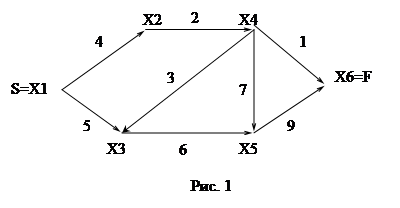


0 комментариев