Навигация
Нейроинформатика и ее приложения
Александр Горбань, gorban@cc.krascience.rssi.ru
Вычислительный центр СО РАН, Красноярск-36
![]()
Что такое нейронные сети?
Задачи для нейронных сетей
Примеры приложений
Истинные преимущества нейронных сетей?
![]()
Каждый, кто впервые знакомится с нейронными сетями, задает себе вопрос: что такое нейроинформатика? Ответить на него можно по-разному. Можно сказать, что нейроинформатика это способ решения всевозможных задач с помощью искусственных нейронных сетей, реализованных на компьютере. Такой ответ, объясняющий только внутреннюю сущность нейроинформатики, почти никого не удовлетворяет, даже если подробно рассказывать о нейронных сетях, задачах и способах их решения. На самом деле требуется еще определить место нейроинформатики среди других способов решения задач и разобраться, в чем же истинные преимущества нейронных сетей, если таковые существуют?
Безусловно, те же самые задачи можно решать и другими способами?
Нейросетевые методы далеко не всегда эффективнее традиционных. К тому же, многие нейросетевые методы это просто новая редакция известных математических подходов.
Почему же тогда многие предпочитают нейросети? Одни чтобы заработать на модной новинке, другие чтобы поиграть в новую интеллектуальную игрушку, не отстать от моды попробовать новую технологию и так далее.
Так в чем же реальные преимущества нейронных сетей? Чтобы ответить на этот вопрос, во-первых, обратимся к десятилетнему опыту применения данной технологии красноярской группой НейроКомп, а во-вторых, попытаемся разгадать логику мирового нейросетевого «бума».
Что такое нейронные сети?
Термин «искусственные нейронные сети» у многих ассоциируется с фантазиями об андроидах и бунте роботов, о машинах, заменяющих и имитирующих человека. Это впечатление усиливают многие разработчики нейросистем, рассуждая о том, как в недалеком будущем, роботы начнут осваивать различные виды деятельности, просто наблюдая за человеком.
Если переключиться на уровень повседневной работы, то нейронные сети это всего-навсего сети, состоящие из связанных между собой простых элементов формальных нейронов. Большая часть работ по нейроинформатике посвящена переносу различных алгоритмов решения задач на такие сети.
В основу концепции положена идея о том, что нейроны можно моделировать довольно простыми автоматами, а вся сложность мозга, гибкость его функционирования и другие важнейшие качества определяются связями между нейронами. Каждая связь представляется как совсем простой элемент, служащий для передачи сигнала. Коротко эту мысль можно выразить так: «структура связей все, свойства элементов ничто».
Совокупность идей и научно-техническое направление, определяемое описанным представлением о мозге, называется коннекционизмом (connection связь). С реальным мозгом все это соотносится примерно так же, как карикатура или шарж со своим прототипом. Важно не буквальное соответствие оригиналу, а продуктивность технической идеи.
С коннекционизмом тесно связан следующий блок идей:
· однородность системы (элементы одинаковы и чрезвычайно просты, все определяется структурой связей);
· надежные системы из ненадежных элементов и «аналоговый ренессанс» использование простых аналоговых элементов;
· «голографические» системы при разрушении случайно выбранной части система сохраняет свои свойства.
Предполагается, что широкие возможности систем связей компенсируют бедность выбора элементов, их ненадежность и возможные разрушения части связей.
Для описания алгоритмов и устройств в нейроинформатике выработана специальная «схемотехника», в которой элементарные устройства (сумматоры, синапсы, нейроны и т.п.) объединяются в сети, предназначенные для решения задач. Для многих начинающих кажется неожиданным, что ни в аппаратной реализации нейронных сетей, ни в профессиональном программном обеспечении эти элементы вовсе не обязательно реализуются как отдельные части или блоки. Используемая в нейроинформатике идеальная схемотехника представляет собой особый язык описания нейронных сетей и их обучения. При программной и аппаратной реализации выполненные на этом языке описания переводятся на более подходящие языки другого уровня.
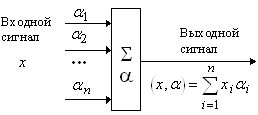
Самый важный элемент нейросистем адаптивный сумматор, который вычисляет скалярное произведение вектора входного сигнала x на вектор параметров a. Адаптивным он называется из-за наличия вектора настраиваемых параметров a.
Нелинейный преобразователь сигнала получает скалярный входной сигнал x и переводит его в заданную нелинейную функцию f(x).
Точка ветвления служит для рассылки одного сигнала по нескольким адресам. Она получает скалярный входной сигнал x и передает его на все свои выходы.
Стандартный формальный нейрон состоит из входного сумматора, нелинейного преобразователя и точки ветвления на выходе.
Линейная связь синапс отдельно от сумматоров не встречается, однако для некоторых рассуждений бывает удобно выделить этот элемент. Он умножает входной сигнал x на «вес синапса» a.
Итак, мы коротко описали основные элементы, из которых состоят нейронные сети. Перейдем теперь к вопросу о формировании этих сетей. Строго говоря, их можно строить как угодно, лишь бы входы получали какие-нибудь сигналы. Обычно используется несколько стандартных архитектур, из которых путем вырезания лишнего или (реже) добавления строят большинство используемых сетей. Для начала следует определить, как будет согласована работа различных нейронов во времени. Как только в системе появляется более одного элемента, встает вопрос о синхронизации функционирования. Для обычных программных имитаторов нейронных сетей на цифровых ЭВМ этот вопрос не актуален только из-за свойств основного компьютера, на котором реализуются нейронные сети. Для других способов реализации он весьма важен. Мы же будем рассматривать только те нейронные сети, которые синхронно функционируют в дискретные моменты времени: все нейроны срабатывают «разом».
В зоопарке нейронных сетей можно выделить две базовых архитектуры слоистые и полносвязные сети.
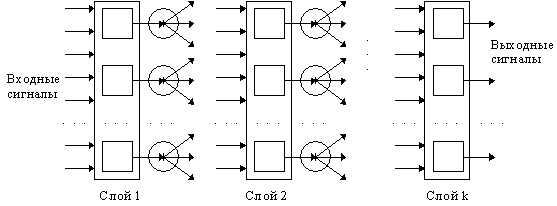
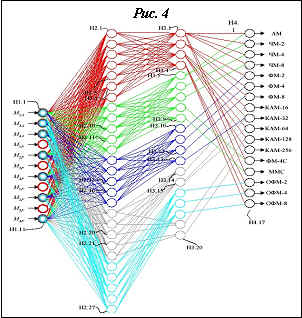
Слоистые сети. Здесь нейроны расположены в несколько слоев. Нейроны первого слоя получают входные сигналы, преобразуют их и через точки ветвления передают нейронам второго слоя. Далее срабатывает второй слой и т.д. до слоя k, который выдает выходные сигналы для интерпретатора и пользователя. Если противное не оговорено, то каждый выходной сигнал слоя i подается на вход всех нейронов слоя i+1. Число нейронов в каждом слое может быть любым и никак заранее не связано с количеством нейронов в других слоях. Стандартный способ подачи входных сигналов: все нейроны первого слоя получают каждый входной сигнал. Особенно широко распространены трехслойные сети, в которых каждый слой имеет свое наименование: первый входной, второй скрытый, третий выходной.
Полносвязные сети. Здесь каждый нейрон передает свой выходной сигнал остальным нейронам, включая самого себя. Выходными сигналами сети могут быть все или некоторые выходные сигналы нейронов после нескольких тактов функционирования сети. Все входные сигналы подаются всем нейронам.
Элементы слоистых и полносвязных сетей могут выбираться по-разному. Существует, впрочем, стандартный выбор: нейрон с адаптивным неоднородным линейным сумматором на входе.
Для полносвязной сети входной сумматор нейрона фактически распадается на два: первый вычисляет линейную функцию от входных сигналов сети, второй линейную функцию от выходных сигналов других нейронов, полученных на предыдущем шаге.
Функция активации нейронов (характеристическая функция) это нелинейный преобразователь выходного сигнала сумматора. Если функция одна для всех нейронов сети, то сеть называют однородной (гомогенной). Если же характеристическая функция зависит еще от одного или нескольких параметров, значения которых меняются от нейрона к нейрону, то сеть называют неоднородной (гетерогенной).
Составлять сеть из нейронов стандартного вида не обязательно. Слоистая или полносвязная архитектуры не налагают существенных ограничений на участвующие в них элементы. Единственное жесткое требование, предъявляемое архитектурой к элементам сети, это соответствие размерности вектора входных сигналов элемента (она определяется архитектурой) числу его входов. Если полносвязная сеть функционирует до получения ответа заданное число тактов k, то ее можно представить как частный случай k-слойной сети, все слои которой одинаковы и каждый из них соответствует такту функционирования полносвязной сети.
Существенное различие между полносвязной и слоистой сетями становится очевидным, когда число тактов функционирования заранее не ограничено слоистая сеть так работать не может.
Доказаны теоремы о полноте: для любой непрерывной функции нескольких переменных можно построить нейронную сеть, которая вычисляет эту функцию с любой заданной точностью. Так что нейронные сети в каком-то смысле могут все.
Задачи для нейронных сетей
Многие задачи, для решения которых используются нейронные сети, могут рассматриваться как частные случаи следующих основных проблем:
· построение функции по конечному набору значений;
· оптимизация;
· построение отношений на множестве объектов;
· распределенный поиск информации и ассоциативная память;
· фильтрация;
· сжатие информации;
· идентификация динамических систем и управление ими;
· нейросетевая реализация классических задач и алгоритмов вычислительной математики: решение систем линейных уравнений, решение задач математической физики сеточными методами и др.
Однозначно построить функцию (обычно многих действительных переменных) по конечному набору значений невозможно без специальных дополнительных условий. В качестве таких условий в классических подходах используются требования минимизации некоторых регуляризирующих функционалов, например, интеграла суммы квадратов вторых производных требование максимальной гладкости. При этом известные в конечном множестве точек значения функции превращаются в набор ограничений, при которых находится минимум функционала.
С помощью нейронных сетей строится, естественно, нейросетевая реализация функции: создается нейронная сеть, которая, получая на входе вектор аргументов, выдает на выходе значение функции. Обычно предполагается, что любая типичная нейросетевая реализация подойдет для решения задачи. При необходимости вместо требования максимальной гладкости минимизируют число слоев, количество нейронов и/или число связей, а также вводят условие «максимально пологой» функции активации нейронов.
Построить функцию по конечному набору значений обычно требуется при решении одной из самых актуальных для пользователей и аналитиков задач: заполнение пропусков в таблицах. Пусть, как обычно, каждая строка таблицы данных соответствует какому-либо объекту, а в строках указаны значения признаков (свойства) соответствующих объектов. В подавляющем большинстве случаев данные неполны: по крайней мере, для части объектов неизвестны значения некоторых признаков. Необходимо как-то восстановить пропущенные значения. Достоверная статистическая оценка должна давать для отсутствующих данных их условное математическое ожидание (условия известные значения других признаков) и характеристику разброса доверительный интервал. Это, однако, требует либо непомерно большого объема известных данных, либо очень сильных предположений о виде функций распределения. Приходится вместо статистически достоверных уравнений регрессии использовать правдоподобные нейросетевые реализации.
Термин «правдоподобные» взят нами из книги Дж. Пойя «Математика и правдоподобные рассуждения». Любая, даже самая строгая математическая конструкция сначала создается всего лишь как правдоподобная гипотеза. Правдоподобными мы называем те выводы, которые еще не прошли испытания на достоверность и строгость, однако именно так совершаются открытия. Кроме того, напомним, что утверждения о статистической достоверности базируются на весьма ограничительных гипотезах о статистической природе эмпирического материала (согласно этой природе данные представляют собой результаты независимых статистических испытаний выбора из фиксированной генеральной совокупности).
Задача классификации также может рассматриваться как задача заполнения пропусков в таблицах: для каждого класса в таблице есть поле, в котором указывается, принадлежит объект данному классу или нет. В эти поля могут помещаться численные значения, например, 1, если объект принадлежит классу, и 0 (или -1) в противном случае.
При обучении классификации с учителем для части объектов, составляющих обучающую выборку, известно, каким классам они принадлежат. Требуется построить нейронную сеть, которая по признакам объекта (записанным в других полях таблицы) определяла бы, к какому классу он принадлежит, т. е. заполняла бы соответствующие поля.
Построение отношений на множестве объектов одна из загадочных и открытых для творчества самых перспективных областей применения искусственного интеллекта. Первый и самый распространенный пример этой задачи классификация без учителя. Допустим, задан набор объектов, причем каждому объекту сопоставлен вектор значений признаков (строка таблицы). Требуется разбить эти объекты на классы эквивалентности. Зачем нужно строить отношения эквивалентности между объектами? В первую очередь для фиксации знаний. Мы накапливаем знания о классах объектов это практика многих тысячелетий, зафиксированная в языке: знание относится к имени класса (пример стандартной древней формы: «люди смертны», «люди» имя класса). В результате классификации появляются новые имена и правила их присвоения. Для каждого нового объекта мы должны сделать две вещи:
Похожие работы
... сети, позволяющая реализовать автоматическое изменение числа нейронов в зависимости от потребностей задачи, позволяет не только исследовать, но и контролировать процесс воспитания психологической интуиции искусственных нейронных сетей. - Впервые применена выборочная константа Липшица для оценки необходимой для решения конкретной задачи структуры нейронной сети. Практическая значимость ...
... экспертных систем (А. Батуро), а также лекции проф. А.Н. Горбаня по нейронным сетям. Приложение 1. Плакаты для защиты диплома. ТЕХНОЛОГИЯ ИЗВЛЕЧЕНИЯ ЗНАНИЙ ИЗ НЕЙРОННЫХ СЕТЕЙ: ¨ АПРОБАЦИЯ, ¨ ПРОЕКТИРОВАНИЕ ПО, ¨ ИСПОЛЬЗОВАНИЕ В ПСИХОЛИНГВИСТИКЕ ЦЕЛЬ РАБОТЫ ¨ апробация гибкой технологии извлечения ...
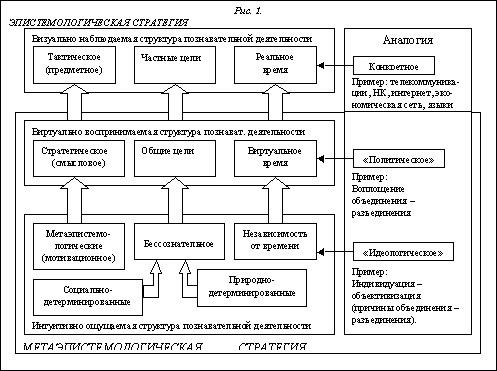
... причине отсутствия какого-либо доминирования в восприятии целого комплекса параметров. В связи с этим попытаемся определить степень однородности проявлений познавательной деятельности в рамках эпистемологической стратегии (ЭС). Стратегия – подчеркивает факт развертывания познания по доминирующему плану, проявляющемуся как в общей структуре познания, так и в частных ее воплощениях. Таким образом, ...
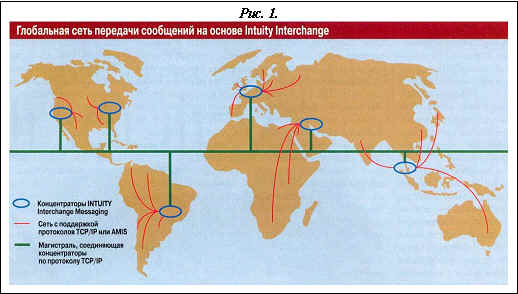
... принято считать, и самым непосредственным образом связана с социальными явлениями 35, а стратегия Internet, таким образом, как социотехнологическая стратегия возникла неявно в самой методологии ЭВМ задолго до появления идеи в умах разработчиков. В связи с этим первым виртуальным нейрокомпьютером можно считать саму математику, которая, как система понятий, определений, связанных ассоциативными и ...

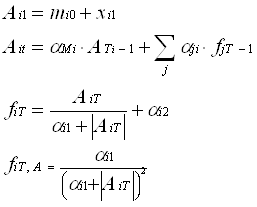
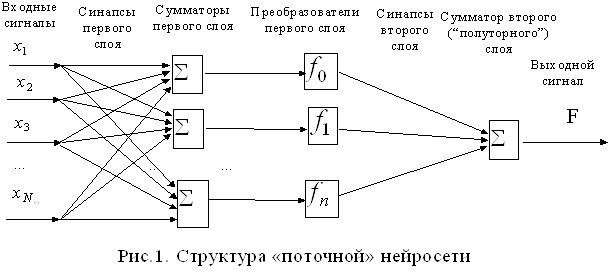


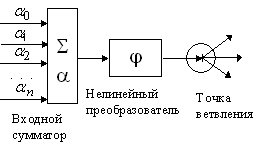

0 комментариев