Навигация
1.1 Введение.
Платоновыми телами (правильными многогранниками) называются такие выпуклые многогранники, все грани которых - правильные многоугольники и все многогранные углы при вершинах равны между собой.
Актуальность разработки программного продукта, позволяющего оперировать с платоновыми телами в качестве графических объектов, подтверждается тем, что в современном программировании графики часто в качестве объектов используются именно многогранники. Современное программное обеспечение предоставляет пользователю большое количество решений этой проблемы. Но преимущество данного программного продукта перед ними заключается в простоте использования, а именно:
не требуется больших затрат ресурсов;
не требуется длительного изучения возможностей программы для получения желаемого результата.
Также программа позволяет реализовать принцип обучения на примерах, т.е. начинающий программист имеет возможность просмотреть все исходные тексты программы, содержащие необходимые пояснения, и разобраться в ее работе наглядно.
1.2 Аналитический обзор.
Существует ровно пять правильных многогранников. Их основные характеристики приведены в следующей таблице:
| Название Многогранника | Число граней | Число ребер | Число вершин |
| Тетраэдр | 4 | 6 | 4 |
| Гексаэдр | 6 | 12 | 8 |
| Октаэдр | 8 | 12 | 6 |
| Додекаэдр | 12 | 30 | 20 |
| Икосаэдр | 20 | 30 | 12 |
Вывод изображения на экран дисплея и разнообразные действия с ним, в том числе и визуальный анализ, требуют от программиста определенной геометрической грамотности. Геометрические понятия, формулы и факты, относящиеся прежде всего к плоскому и трехмерному случаям, играют в задачах компьютерной графики особую роль. Геометрические соображения, подходы и идеи в соединении с постоянно расширяющимися возможностями вычислительной техники являются источником существенных продвижений на пути развития компьютерной графики, ее эффективного использования в научных и иных исследованиях.
Современное программное обеспечение предоставляет программисту широкий спектр возможностей по работе с компьютерной графикой, причем, как с двумерной, так и с трехмерной. В зависимости от поставленной перед программистом задачи и уровня его подготовки, у него есть ряд возможностей при разработке программы для работы с графикой. Во-первых, программист может разработать программный продукт при помощи прямого программирования аффинных преобразований на плоскости и в пространстве. Во-вторых, он может воспользоваться уже созданными библиотеками для моделирования графических объектов (например, библиотека OpenGL). В-третьих, существуют программные продукты, посвященные графическому моделированию и не требующие написания кода программы для работы с графикой (например, 3D-Studio).
Описание математического аппарата аналитической геометрии.Движение графических объектов в пространстве осуществляется посредством аффинных преобразований. Любое аффинное преобразование в трехмерном пространстве может быть представлено в виде суперпозиции вращений, растяжений, отражений и переносов. Каждая точка пространства (кроме начальной точки О) может быть задана четверкой одновреммено не равных нулю чисел (hx, hy,hz,h); эта четверка чисел определена однозначно с точностью до общего множителя.
Рассмотрим матрицы преобразований.
1) Матрицы вращения в пространстве
Матрица вращения вокруг оси абсцисс на угол :
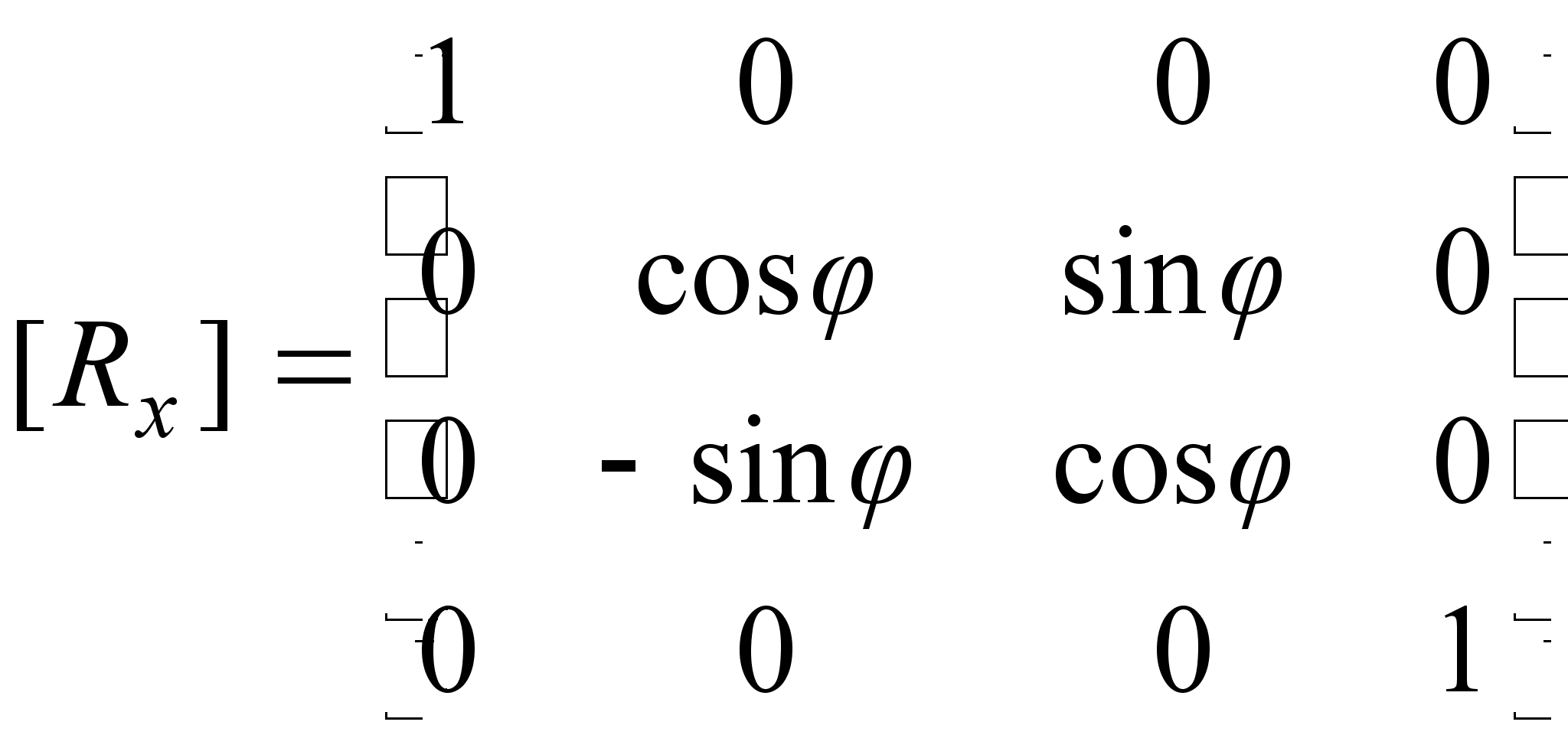
М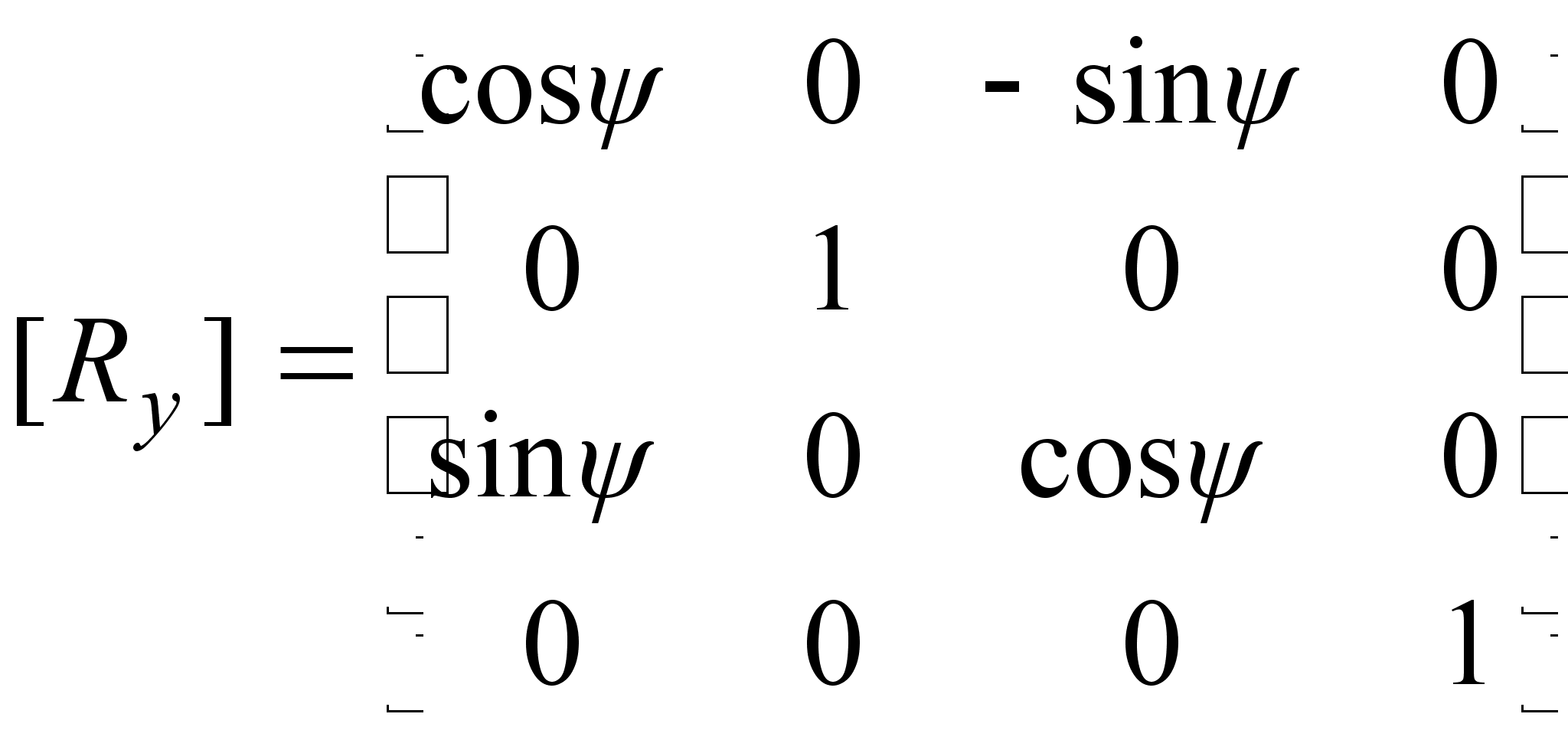
атрица
вращения вокруг
оси ординат
на угол :
Матрица вращения вокруг оси аппликат на угол :
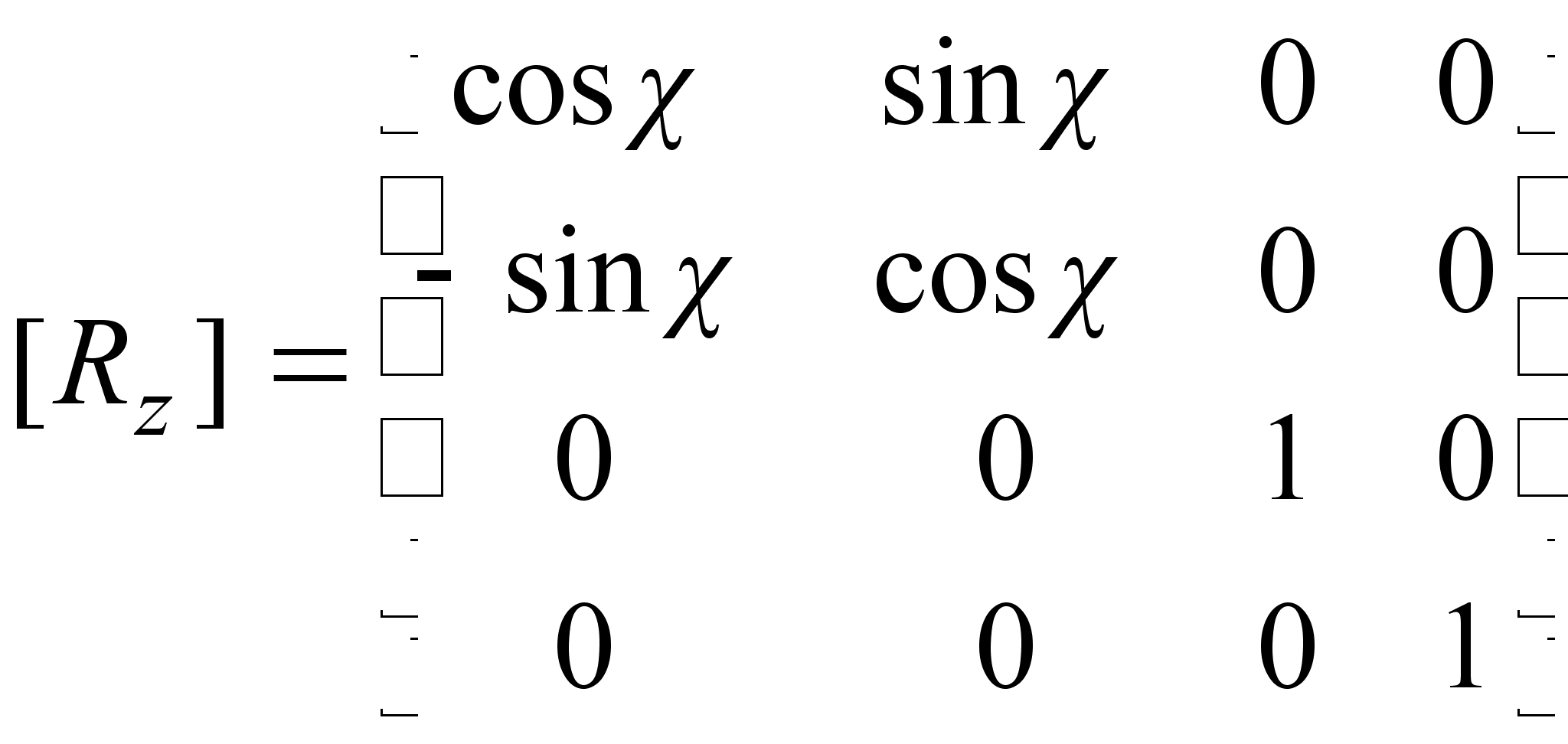
2) Матрица растяжения (сжатия):
г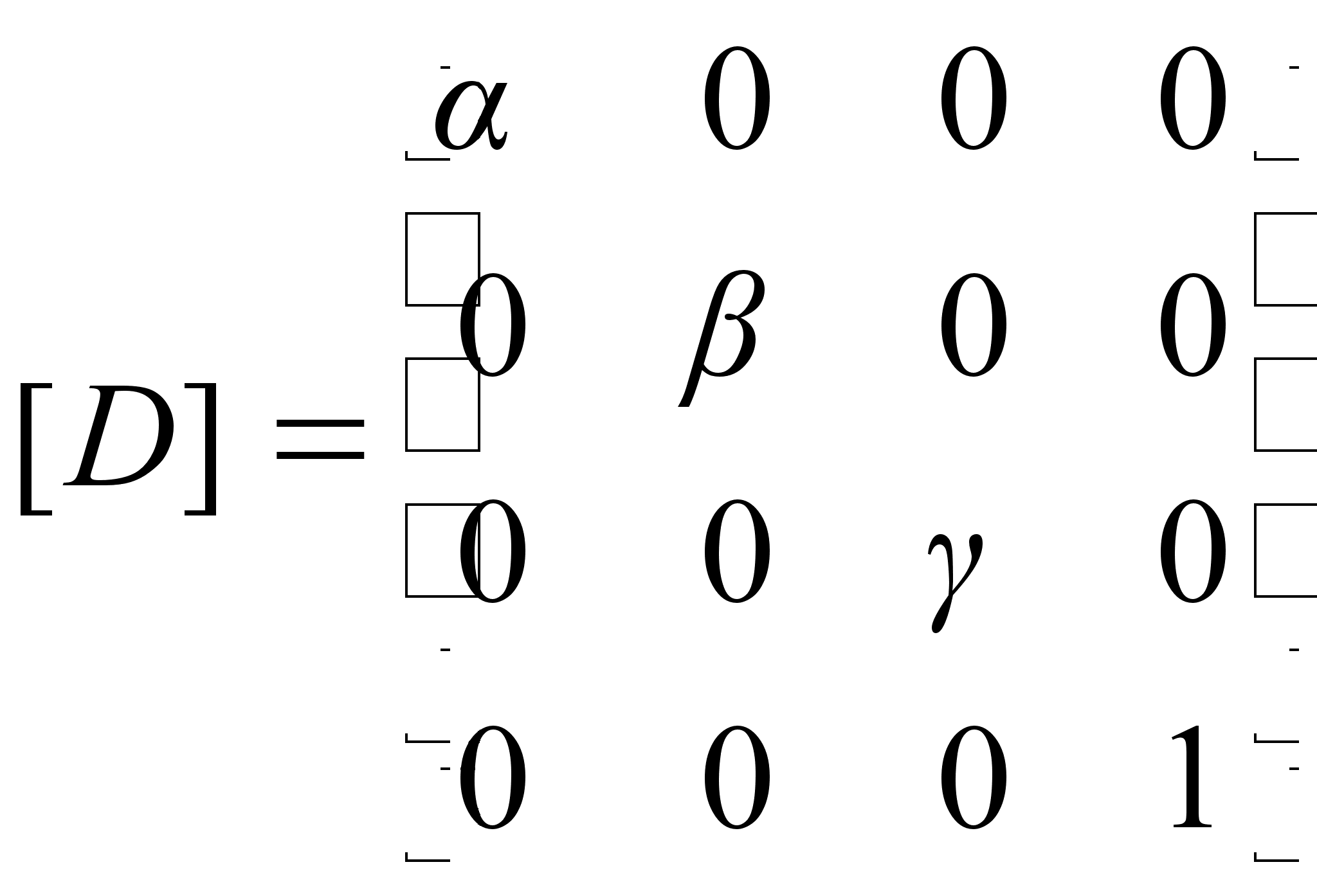
де
>0 – коэффициент растяжения (сжатия) вдоль оси абсцисс;
>0 – коэффициент растяжения (сжатия) вдоль оси ординат;
>0 – коэффициент растяжения (сжатия) вдоль оси аппликат.
3) Матрицы отражения.
М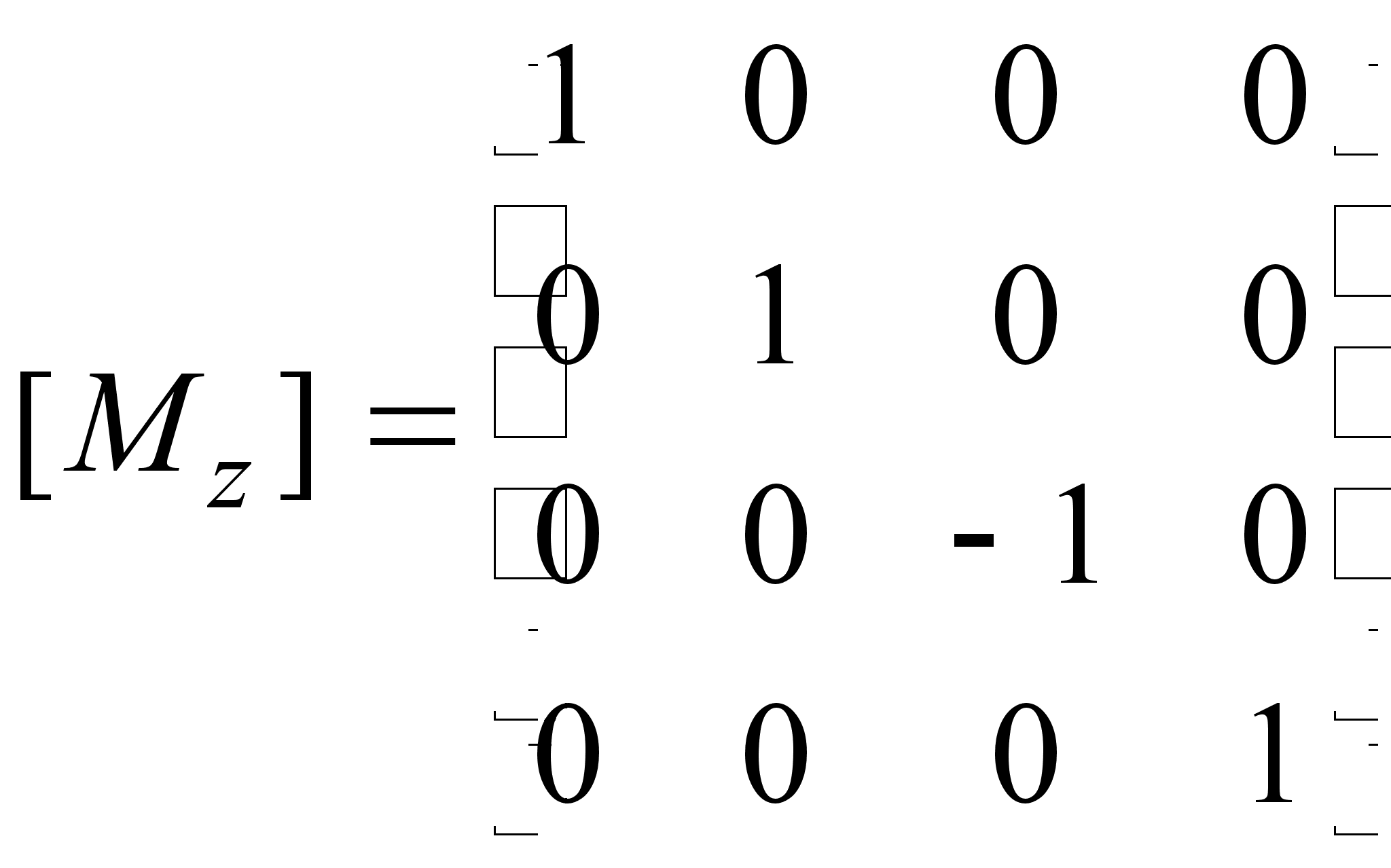
атрица
отражения
относительно
плоскости xy:
М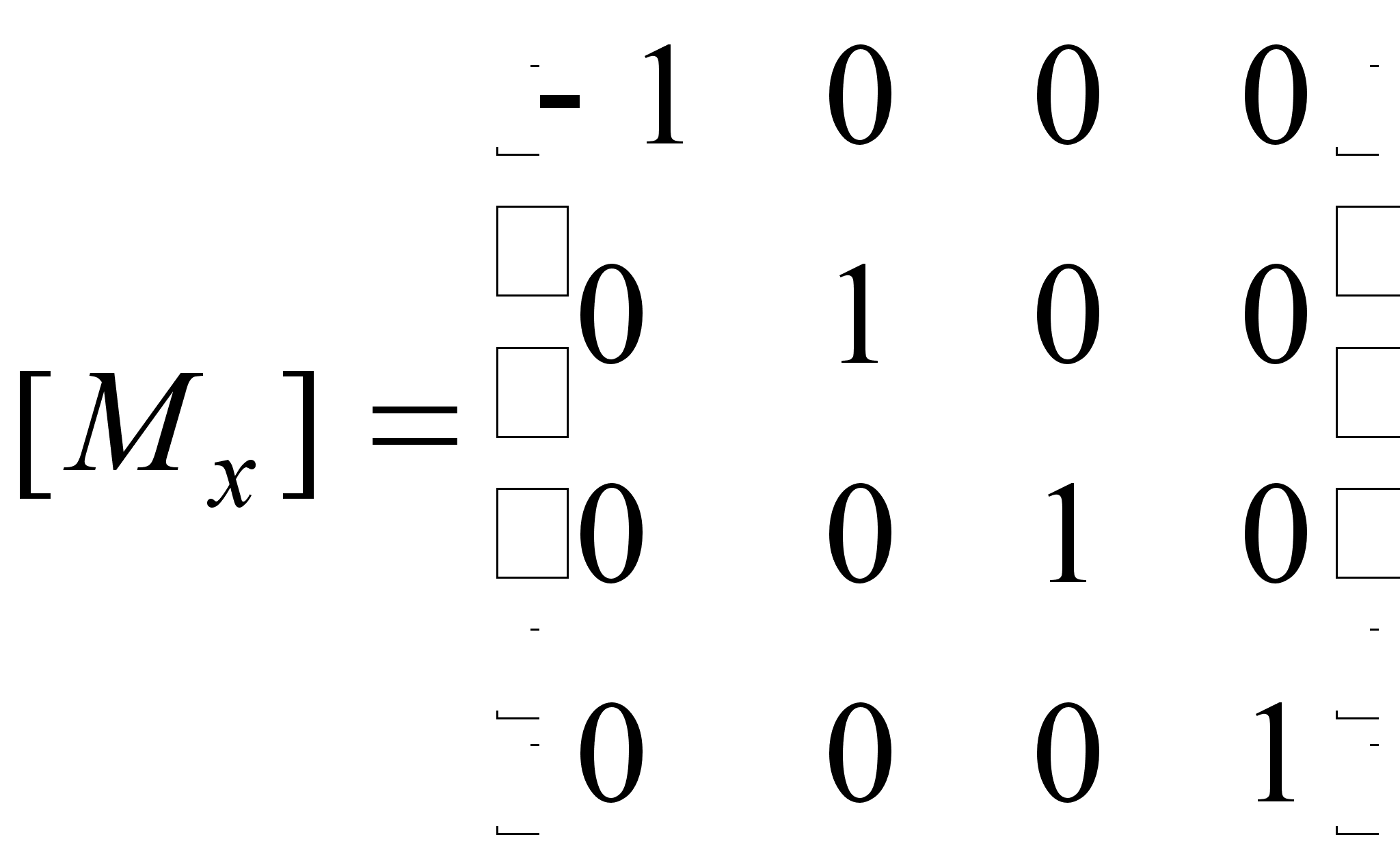
атрица
отражения
относительно
плоскости yz:
М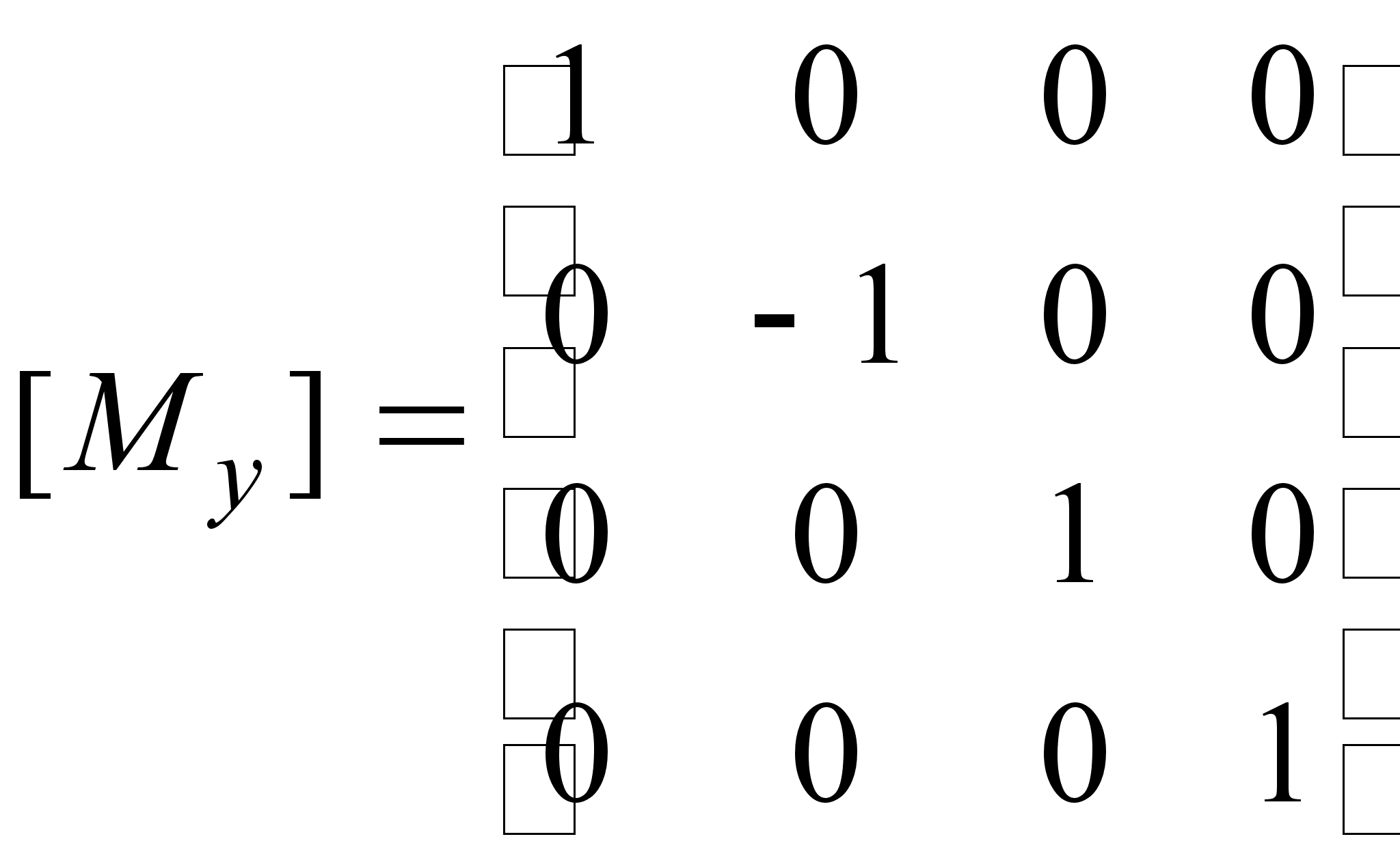
атрица
отражения
относительно
плоскости zx:
4
)
Матрица переноса
где ( - вектор переноса.
Технический и рабочий проекты программного продукта.
Уточнение технических требований, сформулированных в теоретическом задании.Для успешного запуска программы и работы с ней необходимо выполнение ниже перечисленных требований:
IBM-совместимый компьютер с процессором Pentium 90;
VGA видеокарта;
Похожие работы
... представляют собой числа с плавающей точкой. Наличие различных форматов позволяет библиотеке OpenGL принимать данные пользователя в его собственном формате данных. Некоторые команды библиотеки OpenGL допускают использование 8 различных типов данных в качестве своих параметров. Буквы, используемые в качестве суффиксов для того, чтобы определить эти типы данных для реализации ISO С библиотеки ...
... , комментарии в формате XML. Переняв многое от своих предшественников — языков С++, Delphi, Модула и Smalltalk — С#, опираясь на практику их использования, исключает некоторые модели, зарекомендовавшие себя как проблематичные при разработке программных систем: так, C# не поддерживает множественное наследование классов (в отличие от C++) или вывода типов (реализовано в .NET Framework 3.0). C# ...
... согласно заданному алгоритму. Все ошибочные ситуации были рассмотрены, ошибки – устранены. 4. Применение программы 4.1 Назначение программы Программа предназначена для создания и редактирования сложных графических эффектов частиц. В процессе разработки была обеспечена реализация программой следующего набора функций: - управление динамическим набором эмиттеров (систем частиц); - ...
... не обо всех знаю. Скептики, возможно, не поверят мне, когда я скажу, что на Delphi можно одинаково хорошо писать как приложения к корпоративным базам данных, так и, к примеру, игровые программы. Тем не менее, это так. Во многом это объясняется тем, что традиционно в среде Windows было достаточно сложно реализовывать пользовательский интерфейс. Событийная модель в Windows всегда была сложна ...

0 комментариев