Навигация
Сравнение. Два указателя можно сравнивать только на равенство (или неравенство). Можно сравнивать указатель с nil, с адресами переменных
2. Сравнение. Два указателя можно сравнивать только на равенство (или неравенство). Можно сравнивать указатель с nil, с адресами переменных.
С динамическими переменными можно выполнять все действия, разрешённые для статических переменных, например:
if p^ >= q^ then p^ := q^;
Рассмотрим теперь несколько искусственный пример использования динамических переменных: пусть требуется сложить два числа, не используя статических переменных:
var pa,pb: ^real;
begin
new(pa); new(pb);
write('Введите a: '); readln(pa^);
write('Введите b: '); readln(pb^);
writeln('a+b=',pa^+pb^);
dispose(pa); dispose(pb);
readln;
end.
Кроме описанных указателей существуют ещё так называемые нетипизированные указатели (тип pointer), которые могут служить указателями на переменные любых типов, однако необходимость в них возникает редко, поэтому рассматривать их подробно мы не будем.
Динамические структуры данных
|
Вернёмся теперь к вопросу об экономии памяти при хранении табличных данных. С использованием указателей можно отказаться от массива и использовать динамические структуры. Самой простой из них является список, который схематично изображается так:
Прямоугольники на этой схеме – динамические переменные типа запись, Data – поле (или поля), содержащие полезную информацию (например фамилии и номера телефонов), поле, которое изображено ниже Data – это указатель на следующую запись. Переменная List также является указателем на запись. Жирная точка в поле «следующий элемент» в самой последней записи означает, что там лежит значение nil, чтобы показать, что эта запись – последняя в списке.
Для описания списка на Паскале достаточно описать тип указателя на запись и тип самой записи. Выглядит всё это так:
type tItemPtr = ^tItem; {указатель на элемент}
tItem = record
Data: tData; {полезные данные}
Next: tItemPtr; {указатель на следующий элемент списка}
end;
В первой строке этого объявления бросается в глаза использование неопределённого типа tItem. Такое исключение из правил в Турбо Паскале сделано умышленно, в противном случае не было бы возможности строить списки и другие связанные структуры из динамических переменных.
Объявить сам список можно как указатель на элемент: var List : tItemPtr; пока наш список пуст, в List следует положить значение nil. При создании первого элемента будем выполнять действия New(List); List^.Next:=nil.
В списках всегда хранится ровно столько элементов, сколько нужно; если какой-либо элемент данных потерял свою ценность, то его всегда можно удалить из списка; если появились новые данные, то можно добавить новый элемент.
Напишем теперь модуль для работы со списками. В нём содержатся процедуры первоначальной подготовки списка; добавления элемента в начало списка; удаления элемента, следующего за указанным; нахождения элемента с заданным номером; подсчета элементов и очистки списка.
unit Lists;
interface
type tData = record
Name: string[50];
Phone: longint;
end;
tItemPtr = ^tItem;
tItem = record
Data: tData;
Next: tItemPtr;
end;
procedure InitList(var l: tItemPtr);
procedure AddItemToHead(var l: tItemPtr; d: tData);
function DeleteItemAfter(var l: tItemPtr; num: word): boolean;
function Count(l: tItemPtr): word;
function GetItem(l: tItemPtr; num: word; var d: tData): boolean;
procedure ClearList(var l: tItemPtr);
{---------------------------------------------------------------}
implementation
procedure InitList(var l: tItemPtr);
begin l:=nil end;
procedure AddItemToHead(var l: tItemPtr; d: tData);
var p: tItemPtr;
begin
new(p);
p^.data:=d;
p^.next:=l;
l:=p;
end;
function DeleteItemAfter(var l: tItemPtr; num: word): boolean;
var p,q: tItemPtr;
i: word;
begin
i:=1;
p:=l;
while (i<>num)and(p<>nil) do begin
i:=i+1;
p:=p^.next;
end;
if p<>nil then begin
if p^.next<>nil then begin
q:=p^.next^.next;
dispose(p^.next);
p^.next:=q;
DeleteItemAfter:=true;
end
else DeleteItemAfter:=false; {не удалён}
end
else DeleteItemAfter:=false;
end;
function Count(l: tItemPtr): word;
var p: tItemPtr;
i: word;
begin
i:=0;
p:=l;
while p<>nil do begin
i:=i+1;
p:=p^.next;
end;
count:=i;
end;
function GetItem(l: tItemPtr; num: word; var d: tData): boolean;
var p: tItemPtr;
i: word;
begin
i:=1;
p:=l;
while (i<>num)and(p<>nil) do begin
i:=i+1;
p:=p^.next;
end;
if p<>nil then begin
d:=p^.data;
GetItem:=true;
end
else GetItem:=false;
end;
procedure ClearList(var l: tItemPtr);
var p: tItemPtr;
begin
while (l<>nil) do begin
p:=l^.next;
dispose(l);
l:=p;
end;
end;
end.
Лекция 16. Динамические переменные: другие виды списков, стек и очередь. 1. Другие виды списковКроме рассмотренных списков возможны более сложные варианты, связанные с наличием двух дополнительных свойств:
1. Двунаправленность списка. В каждом элементе таких списков есть не только указатель на следующий элемент, но и на предыдущий. Такая организация может оказаться полезной при добавлении или удалении элемента, предшествующего указанному.
2. Замкнутость списка. Поле next в последнем элементе указывает на первый элемент. Иначе такие списки называются кольцевыми. Этот вид позволяет упростить процедуру удаления элемента списка и другие операции.
С учётом этих свойств возможны четыре различных типа списков.
Для примера рассмотрим описание и реализацию кольцевого двунаправленного списка:
type tItemPtr = ^tItem
tItem = record
data: tData;
next,prev: tItemPtr;
end;
var List: tItemPtr; {список - указатель на один из элементов}
........
{Удалить после указанного:}
procedure DelAfter(p: tItemPtr);
var q: tItemPtr;
begin
if (p<>nil)and(p^.next<>p) then begin
q:=p^.next^.next;
dispose(p^.next);
p^.next:=q;
q^.prev:=p;
end;
end;
{Вставить перед указанным:}
procedure InsertBefore(p: tItemPtr; d: tData);
var q: tItemPtr;
begin
if p<>nil then begin
new(q);
q^.data:=d;
q^.next:=p;
q^.prev:=p^.prev;
p^.prev:=q;
q^.prev^.next:=q;
end;
end;
2. Стек и очередьСтеком называется такой способ хранения данных, при котором элемент, записанный в хранилище данных, последним всегда извлекается первым (дисциплина LIFO – «last in - first out»). При извлечении элемента происходит его удаление со стека.
Рассмотрим простейший пример использования стека. Предположим, что имеется строка, состоящая из одних лишь открывающих и закрывающих скобок. Требуется определить, является ли она правильным скобочным выражением (то есть для каждой открывающей скобки должна найтись закрывающая). Заведём массив и переменную для хранения номера последнего значимого элемента в массиве (то есть вершины стека), в который при проходе по строке будем складывать все открывающиеся скобки (с увеличением номера вершины на 1), а при встрече с закрывающей будем удалять соответствующую открывающую (попросту уменьшать номер вершины стека). Если окажется, что «пришла» закрывающая скобка, а стек пуст (то есть номер вершины равен 0), то выражение ошибочно. Это же можно сказать и в случае, когда строка закончилась, а стек не пуст.
Очевидно, что для реализации такого стека массив использовать не обязательно, достаточно хранить в некоторой переменной лишь число открывающих скобок. При поступлении закрывающей скобки из этой переменной вычитается 1. Ошибка возникает, если значение переменной стало отрицательным, или при достижении конца строки оно не равно нулю.
Для данных более сложного вида стек можно организовать с помощью однонаправленного некольцевого списка. Чтобы положить элемент в стек, нужно добавить его в начало списка, чтобы извлечь со стека – получить данные первого элемента, после чего удалить его из списка.
Любая реализация стека должна содержать следующие процедуры и функции:
procedure InitStack – инициализация стека;
procedure Push(d: tData) – положить элемент в стек;
procedure Pop(var d: tData) – извлечь элемент с вершины стека;
function NotEmpty: boolean – проверка стека на пустоту;
Очередь отличается от стека тем, что последний пришедший в неё элемент будет извлечён последним, а первый – первым («FIFO»). С помощью списков её можно организовать следующим образом: будем хранить не только указатель на «голову» списка, но и на «хвост»; добавлять будем в «хвост», а извлекать – из «головы».
Любая реализация очереди (не обязательно с помощью списков) должна «уметь» выполнять такие действия:
procedure InitQueue – инициализация очереди;
procedure AddQueue(d: tData) – поставить элемент в очередь;
procedure SubQueue(var d: tData) – извлечь элемент из очереди;
function NotEmpty: boolean – проверка очереди на пустоту;
Лекция 17. Деревья и поиск в деревьях| |
Деревьями называются структуры данных следующего вида:
Элементы дерева называются вершинами. Вершина Tree^ называется корнем дерева, а всё множество вершин, связанных с некоторой вершиной с помощью одного из указателей называется поддеревом. Вершины, у которых все указатели равны nil, иногда называют листьями.
Подробнее мы рассмотрим вариант двоичного дерева, то есть такого, в котором каждая вершина имеет два поддерева (любое из них может оказаться пустым). Такие деревья оказываются очень удобными для решения задачи поиска, когда ключи для наших данных (например фамилии при поиске телефонных номеров) можно сравнивать на "=", "<" и ">". В каждую вершину дерева заносится элемент данных, причём делается это таким образом, чтобы для любой вершины все ключи данных (или сами данные в простейшем случае) из левого поддерева были меньше ключа этой вершины, а все ключи из правого – больше. Выполнения такого требования можно достигнуть при последовательном добавлении элементов (то есть построении дерева, начиная с «нуля», точнее с nil).
При описанном построении дерева поиск оказывается довольно простым делом: сначала мы сравниваем искомый ключ с ключом корня дерева. Если эти два ключа совпадают, то элемент найден, в противном случае выполняем поиск в левом поддереве, иначе – в правом, далее в выбранном поддереве вновь выполняем сравнение его корня с искомым ключом, и т. д. Этот процесс закончится либо когда мы нашли ключ, либо когда очередное поддерево оказалось пустым (это означает, что такой ключ в дереве отсутствует).
Для реализации двоичного дерева сначала рассмотрим его описание на Паскале:
type tNodePtr = ^tNode; {указатель на вершину}
tNode = record
data: tMyData;
left,right: tNodePtr;
end;
tTree = tNodePtr; {для доступа к дереву достаточно хранить
указатель на его корень}
Под данными (tMyData) будем понимать запись, состоящую из ключа, необходимого для сравнений, и собственно данных:
type tMyData = record
key: tKey;
data: tData;
end;
Для того чтобы реализовать действия с двоичным дерево, нам понадобятся так называемые рекурсивные процедуры. Функция или процедура называется рекурсивной, если она вызывает сама себя. Такой вариант рекурсии называется прямым. Кроме того, бывает и косвенная рекурсия, когда одна процедура вызывает другую, а та в свою очередь вызывает первую.
В качестве примера рассмотрим функцию для вычисления факториала, в которой мы заменим цикл (или итерацию) рекурсией. Её идея проста: если аргумент равен нулю, то возвращаем значение 1, в противном случае возвращаем значение аргумента, умноженное на факториал (то есть ту же функцию) от числа, на единицу меньшего. На Паскале всё это будет выглядеть следующим образом:
function factorial(x: byte): longint;
begin
if x=0 then factorial:=1
else factorial:=x*factorial(x-1);
end;
Подобным образом можно применить рекурсию для вычисления n-го числа Фибоначчи, хотя этот способ требует много лишних действий:
function fib(n: integer): integer;
begin
if n<=1 then fib:=1 else fib:=fib(n-1)+fib(n-2);
end;
Косвенная рекурсия может появиться, например при проверке правильности арифметических выражений. Подробно рассматривать этот вопрос сейчас мы не будем.
Возвращаясь к деревьям, заметим, что добавление элемента является рекурсивной процедурой:
procedure InsertNode(t: tTree; key: tKey; data: tData);
begin
if t=nil then begin
new(t);
t^.key:=key;
t^.data:=data;
end
else if key<t^.key then InsertNode(t^.left,key,data)
else InsertNode(t^.right,key,data);
end;
После того как дерево построено, можно выполнять поиск (также рекурсивный):
function Search(t: tree; key: tKey; var data: tData): boolean;
{возвращает значение найден / не найден}
begin
if t=nil then Search:=false
else if key = t^.key then begin
data:=t^.data;
Search:=true;
end
else if key<t^.key then Search:=Search(t^.left,key,data)
else Search:=Search(t^.right,key,data);
end;
Легко заметить, что элементы данных, «уложенные» в двоичное дерево можно выводить в отсортированном порядке:
procedure Traversal(t: tTree); {обход дерева}
begin
if t<>nil then begin
Traversal(t^.left);
writeln('Key:',t^.key,' Data:',t^.data);
Traversal(t^.right);
end;
end;
Лекция 18. Таблицы и простейшие алгоритмы поиска. 1. Определения и описания структур данныхТаблицей будем называть структуру данных, пригодную для хранения набора данных, имеющих одинаковые типы. Простейшим примером такой структуры может служить массив, поскольку тип всех его элементов один и тот же. Чаще всего элемент таблицы состоит из нескольких частей, одна из которых имеет наибольшее значение (называется ключом), а остальные содержат информацию, связанную с этим ключом, или собственно данные. Если всё это изобразить графически, то получится то, что называется таблицей в обычном смысле:
| Ф. И. О. | Адрес | Телефон | Год рождения |
| Петров Ф. М. | Северная 99-88 | 29-29-29 | 1962 |
| Иванов П. С. | Мира 111-222 | 77-88-99 | 1976 |
| Козлов Н. В. | Октябрьская 135-246 | 45-67-89 | 1970 |
| ................. |
Здесь ключом является фамилия, а все остальные элементы — полезная информация о человеке с такой фамилией. В случае, когда наша таблица становится довольно большой, найти данные о нужном нам человеке становится довольно сложно. Алгоритмы, предназначенные для поиска в таблице данных с указанным ключом, называются алгоритмами поиска. Поиск может быть удачным (если элемент с искомым ключом имеется в массиве) и неудачным (в противном случае).
При использовании языка Паскаль для работы с табличными данными довольно удобно использовать записи в качестве элементов данных. В нашем примере таблица будет состоять из элементов следующего типа:
type tItem {элемент} = record
surname: string[30]; {фамилия, ключевое поле}
address: string; {адрес}
phone: longint; {телефон}
birth: word; {год рождения}
end;
При рассмотрении алгоритмов поиска мы будем пользоваться более общей формой для записи типа элемента:
type tItem = record
key: tKey; {ключ}
data: tData; {данные}
end;
Типы tKey и tData зависят от конкретной задачи, которую нужно решать. В нашем примере tKey — строка до 30 символов длиной, а tData можно сделать записью из трёх полей (address, phone и birth).
Рассмотрим теперь некоторые способы реализации всей таблицы:
1. МассивЭто наиболее простой вариант и довольно удобный, поскольку положение элемента в таблице однозначно определяется номером элемента в массиве. Если размер таблицы меняется в ходе работы с ней (данные время от времени добавляются или удаляются), то массив оказывается не очень экономичным: поскольку точное количество элементов заранее неизвестно, приходится заводить массив из большого количества элементов, часть из которых не будет использоваться, но будет занимать место в памяти.
Для того чтобы хранить таблицу, нам потребуется запись из двух полей: сам массив и целочисленное поле, обозначающее текущий размер массива:
const maxsize = 2000; {максимальный размер таблицы}
type tTable = record
a: array[1..maxsize] of tItem; {это сам массив}
n: integer; {а это - реальное число элементов}
end;
var Table: tTable;
Предполагается, что в любой момент времени данные таблицы хранятся в первых n элементах массива, а остальные считаются пустыми.
2. СписокЭтот вариант более экономичен в плане расхода памяти, так как всегда будет занято ровно столько места, сколько нужно под данные. В отличие от массива, мы не можем легко просматривать данные произвольного элемента, для перехода от одного элемента к другому нужно долго двигаться по цепочке указателей; это является недостатком списка.
Как выглядит такая таблица на Паскале нам уже известно:
type tItemPtr = ^tItem; {указатель на элемент списка}
tItem = record {элемент списка}
key: tKey;
data: tData;
next: tItemPtr;
end;
tList: tItemPtr; {задаётся указателем на первый элемент}
var Table: tList {таблица является списком}
3. ДеревоКак хранить и искать данные в двоичном дереве, мы уже знаем, а таблицу можно задать так:
type tItemPtr = ^tItem; {указатель на элемент}
tItem = record {элемент}
key: tKey;
data: tData;
left, right: tItemPtr;
end;
tTree = tItemPtr;
var Table: tTree; {таблица является деревом}
2. Алгоритмы 1. Линейный поиск в массивеПусть таблица представлена в виде массива. Тогда первое, что приходит в голову по поводу поиска элемента — это обход всех элементов, начиная с первого, до тех пор, пока не будет найден элемент с искомым ключом, или пока массив не кончится. Такой способ называется линейным поиском в неупорядоченном массиве. Оформим его на Паскале в виде процедуры:
procedure LinearSearch(var T:tTable; k:tKey; var index:integer);
var i: integer;
begin
i:=1; index:=0;
while (i<=T.n)and(index=0) do begin
if T.a[i].key=k then index:=i;
i:=i+1;
end;
end;
Рассмотрим подробнее части этой процедуры. Параметрами процедуры являются таблица (T), в которой нужно искать элемент, искомое значение ключа (k) и выходной параметр (index), в котором процедура должна указать номер элемента, если он найден, и 0 в противном случае. В списке параметров таблица T описана как параметр переменная, хотя процедура и не должна менять какие-либо данные из таблицы. Это нужно для того, чтобы не создавать копию таблицы в стеке при передаче параметра процедуре, поскольку таблица может иметь большой размер.
Возможен более рациональный вариант: вместо того чтобы всякий раз проверять, не закончился ли массив, можно использовать массив с фиктивным элементом номер 0, перед поиском записывать в него искомое значение ключа, и двигаться по массиву от последнего элемента к первому. Такой способ называется линейным поиском с барьером (барьер — нулевой элемент):
procedure LinearSearch2(var T:tTable; k:tKey; var index:integer);
var i: integer;
begin
T.a[0]:=k;
index:=T.n; index:=0;
while T.a[index]<>k do index:=index-1;
end;
В таком варианте становится значительно меньше сравнений, следовательно, алгоритм работает быстрее предыдущего.
2. Двоичный поискСледующий алгоритм также применяется для таблицы, представленной в виде массива, кроме того, массив должен быть отсортированным по значениям ключа (для определённости — по возрастанию). Тогда при поиске можно использовать следующие соображения: возьмём элемент, находящийся в середине массива, если его ключ равен искомому ключу, то мы нашли нужный элемент, если меньше — продолжаем поиск в первой половине массива, если меньше — то во второй. Под продолжением понимаем аналогичный процесс: вновь берём средний элемент из выбранной половины массива, сравниваем его ключ с искомым ключом, и т. д. Этот цикл закончится, когда часть массива, в которой производится поиск, не будет содержать ни одного элемента. Так как этот алгоритм многократно разбивает массив на две части, то он называется алгоритмом двоичного поиска. Ниже приведена соответствующая процедура на Паскале.
procedure BinarySearch(var T:tTable; k:tKey; var index:integer);
var l,c,r: integer;
begin
index:=0;
l:=1; r:=T.n;
while (index=0)and(l<=r) do begin
c:=(l+r) div 2;
if T.a[c].key=k then index:=c
else if T.a[c].key>k then r:=c-1
else l:=c+1;
end;
end;
Переменные l, r и c обозначают соответственно номер левого края, центра и правого края части массива, в которой мы ищем элемент с заданным ключом. Поиск прекращается либо если элемент найден (index <> 0), либо если часть массива, в которой нужно искать, была исчерпана (то есть номер левого края превысил номер правого). Внутри цикла находим номер середины части массива (c), затем сравниваем ключ этого среднего элемента с искомым ключом. Если выполнилось равенство, то элемент найден, если средний больше искомого, то устанавливаем правую границу части массива равной c-1, если больше — меняем левую границу на c+1.
3. Линейный поиск в спискеПусть теперь данные таблицы содержатся в списке. В этом случае можно использовать для поиска алгоритм, очень похожий на алгоритм линейного поиска в массиве. Отличие лишь в том, что изменение номера текущего элемента заменяется переходом к указателю на следующий элемент списка:
procedure SearchInList(T: tTable; k: tKey; var p: tItemPtr);
var notfound: boolean;
begin
notfound:=true;
p:=T;
while (p<>nil) and (notfound) do begin
if p^.key=k then notfound:=false;
p:=p^.next;
end;
end;
Параметр T в этом случае не нужно делать параметром-переменной, поскольку он является только указателем на начало таблицы, а сама таблица лежит в динамической памяти. Вместо номера найденного элемента будем возвращать пользователю нашей процедуры указатель на него (если поиск был удачным) или nil, если поиск неудачен.
Сокращать число проверок в цикле с помощью барьера было бы неразумно: каждый раз барьер придётся ставить в «хвост» списка, а для этого нужно сначала обойти весь список, начиная с головы, затрачивая при этом много времени.
Лекция 19. Перемешанные таблицыНаиболее очевидным способом хранения таблицы является массив, в котором несколько первых элементов представляют собой полезные данные, а остальные элементы считаются пустыми. Ниже будет рассмотрен другой вариант применения массива для реализации таблицы.
Позволим данным располагаться в любых элементах массива, а не только в первых n. Чтобы отличать пустые элементы от занятых нам понадобится специальное значение ключа, которое мы будем заносить в ключевое поле всех пустых ячеек. Если ключ — число, а все полезные ключи положительны, то можно в качестве ключа пустой ячейки использовать 0, если ключи — строки, содержащие фамилии, то ключом пустой ячейки можно сделать пустую строку и т. п. Пусть в ключами являются строки, тогда для таблицы потребуются такие объявления:
const empty = '';
nmax = 1000;
type tKey = string;
tData = .....;
tItem = record
key: tKey;
data: tData;
end;
tTable = array[0..nmax-1] of tItem;
Перед тем как помещать данные в массив заполним ключевые поля всех его элементов «пустыми» значениями. Заносить в таблицу будем не все данные сразу, а один за другим, по очереди. Для того, чтобы определить номер ячейки массива, в которую нужно поместить добавляемый элемент данных, напишем функцию, значение которой зависит только от ключа добавляемого элемента. В такой ситуации поиск можно будет осуществлять довольно просто: находим значение функции на искомом ключе, и смотрим на элемент массива с полученным номером. Если ключ элемента равен искомому ключу, мы нашли то, что искали, иначе — поиск оказался неудачным.
Реализованная описанным способом таблица называется перемешанной (или hash-таблицей), а функция — функцией расстановки ключей (hash-функцией). Такие названия связаны с тем, что данные беспорядочно разбросаны по массиву.
Теперь покажем, как всё сказанное воплотить в программу на Паскале. В качестве ключей в наших примерах используются строки, поэтому можно предложить такой вариант хэш-функции: сложить коды всех символов строки, и, чтобы полученное число не выходило за максимально возможный индекс массива, возьмём остаток от деления на размер массива:
function hash(key: tKey): integer;
var i: integer;
begin
sum:=0;
for i:=1 to length(key) do sum:=sum+ord(key[i]);
hash := sum mod nmax;
end;
Процедура добавления элемента в таблицу в предварительном варианте будет выглядеть так:
procedure AddItem(var t: tTable; item: tItem);
var h: integer;
begin
h:=hash(item.key);
t[h]:=item.key;
end;
У написанной процедуры есть один существенный недостаток: если элемент, номер которого указала нам хэш-функция был занят, то новые данные будут записаны на место старых, а старые бесследно исчезнут. Чтобы решить эту проблему будем пытаться найти какой-либо другой свободный элемент для добавляемых данных. Здесь понадобится ещё одна функция (вторичная хэш-функция), которая по номеру занятого элемента и по значению ключа добавляемых данных укажет номер другой ячейки, если и там будет занято, вызовем вторичную функцию ещё раз, и т. д. до тех пор пока свободная ячейка не найдется.
Наиболее простая хэш-функция будет добавлять к номеру занятой ячейки какое-нибудь постоянное число:
const HC = 7;
function hash2(n: integer, key: tKey): integer;
begin
hash2 := (n + HC) mod nmax;
end;
Остаток от деления на nmax понадобилось вычислять по той же причине, что и в первичной хэш-функции.
Сейчас можно написать окончательный вариант процедуры добавления элемента данных в таблицу:
procedure AddItem(var t: tTable; item: tItem);
var h: integer;
begin
h:=hash(item.key);
while t[h].key<>empty do h:=hash2(h,item.key);
t[h].key:=item.key;
t[h].data:=item.data;
end;
Пусть в хэш-таблицу занесены все необходимые данные и требуется отыскать данные с некоторым ключом. Для этого будем действовать по такой схеме: вычисляем значение хэш-функции на данном ключе, если ячейка с полученным номером свободна, то элемент не найден, если занята, то сравниваем её ключ с искомым. В случае совпадения мы нашли нужный элемент, иначе — находим значение вторичной функции и смотрим на ключ в ячейке с полученным номером. Если он равен «пустому» значению, то поиск неудачен, если равен искомому ключу — то удачен, иначе — вновь находим значение вторичной хэш функции и т. д. На Паскале всё это выглядит так:
const notfound = -1;
continue = -2;
procedure Search(var t: tTable; key: tKey; var index: integer);
var h: integer;
begin
h:=hash(key);
index:=continue;
repeat
if t[h].key = key then index:=h
else if t[h].key = empty then index:= notfound
else h:=hash2(h,key);
until index<>сontinue;
end;
Процедура выдаёт ответ о результатах поиска через параметр-переменную index. При удачном поиске там будет лежать номер найденного элемента, при неудачном — константа notfound. Константа continue означает «пока не найден» и используется только внутри процедуры. При поиске сначала вычисляется значение первичной хэш-функции, а в index заносится значение continue Затем выполняется проверка на равенство ключей, если оно выполняется, то ячейка массива найдена, и мы записываем её номер в index, иначе, если ячейка пуста, то элемент не найден (в index записываем notfound), в третьем случае находим значение вторичной функции. Эти действия продолжаются до тех пор, пока index не перестанет быть равным continue.
Похожие работы
... , тем не менее, использование программ с перекрытиями снимает это ограничение. Два библиотечных модуля TURBO3 и GRAPH3 введены для совместимости с ранней версией 3.0 системы Турбо Паскаль. 2 Объекты Базовым в объектно-ориентированном программировании является понятие объекта. Объект имеет определённые свойства. ...
... выбрать режим Quit <Alt>-<X>, после чего нажать либо <Enter>, либо комбинацию <Alt>-<X>. ФУНКЦИОНАЛЬНЫЕ КЛАВИШИ Функциональные клавиши используются для управления средой Турбо Паскаля. Они обозначаются F1, F2,..., F12 и располагаются в самом верхнем ряду клавиатуры. С каждой из этих клавиш связывается некоторая команда меню. Действие почти всех функциональных ...
... X. При успешном результате e=0. ПРОЦЕДУРЫ И ФУНКЦИИ Турбо Паскаль позволяет выделять фрагменты программы во вспомогательные алгоритмы (ВА). Это позволяет писать хорошо структурированные программы. Языки программирования, в которых предусмотрены ВА, называются процедурно-ориентированными. Структурированные программы обычно проще в понимании и отладке. Наличие ВА в языке программирования ...
... программы необходимо располагать ее спецификацию – комментарий в фигурных скобках, содержащий назначение программы, данные о программисте, дату создания программы. Язык программирования Паскаль является языком структурного программирования. В нем есть все необходимые управляющие конструкции для структурного построения программы. Наглядность такому построению придает структуризация внешнего вида ...

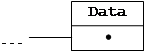

0 комментариев