Навигация
Поиск по статистическому градиенту
3.4. Поиск по статистическому градиенту.
Пусть надо найти максимум . В точке делается m случайных испытаний и вычисляются приращения целевой функции
где - случайные величины, - случайный шаг.
Далее определяют величину
Усредненное по всем реализациям значения совпадает с истинным направлением наискорейшего подъема, т. е.
Далее из точки совершается очередной рабочий шаг:
3.5. Метод “тяжелого шарика”.
Рассмотрим простейший вариант случайного поиска:
пусть - произвольная точка. Из совершается движение с шагом в случайном направлении с равномерным распределением.
Движение представляющей точки описывается так:
Этот алгоритм без памяти может быть усовершенствован. Направление удачных проб запоминается и вероятность шага в этих направлениях возрастает. Для этого введем вектор памяти , проекции которого на координатные оси определяют вероятность выбора положительного направления по i - ой оси. - монотонная, неубывающая функция, тогда , а изменяется так:
где - параметр запоминания, - характеризует скорость обучения, .
Этот метод называется методом “тяжелого шарика”.
3.6. Формирование маршрутной матрицы.
Пусть поставлена задача (2.3) - (2.4). Для нахождения решения применим метод последовательной оптимизации.
Описание метода.
1. Начальный шаг к=0.
В качестве начального приближения выберем некоторую матрицу . Матрица должна удовлетворять условиям 2.4. Зададим точность .
Замечание. Выше было сказано, что для того, чтобы повысить вероятность нахождения глобального экстремума выбирают несколько начальных приближений. может быть выбрана случайно, либо область определения может быть разбита на интервалы и в качестве выбираются узлы полученной сетки. Методы выбора числа случайных проб или размерности сетки описаны в [3] - [7].
2. к-ый шаг. Выбор направления движения.
Для каждого элемента , где вычислим значения целевой функции , где - матрица, в которой все элементы равны элементам матрицы , кроме одного этого элемента , который равен . Значение величины выбирается из соображений о точности, с которой ищется . Методы выбора величины описаны в [3] - [7].
Таким образом получим множество значений целевой функции . ( может быть положительной и отрицательной). Для всех элементов . Выберем теперь . Соответствующий элемент матрицы запоминаем. Пусть это будет .Выберем теперь в строке i1 элемент , такой, что . Запомним также этот элемент.
Рассмотрим два возможных варианта:
а) Если , то запоминаем компоненты , и переходим к 3.
б) Если , то , переходим к 4.
3. к-ый шаг. Движение в выбранном направлении.
Из точки переходим к следующим образом:
Если , то определяется следующим образом:
к:=к+1, переходим к 3.
Если , то , к:=к+1, переходим к 2.
4. Конечный шаг.
Если ( - величина, определяющая точность вычисления экстремума), то - искомая маршрутная матрица.
Если , то выбирают другое начальное приближение и переходят к 2. Если множество начальных приближений исчерпано, то полагают, что сформировать маршрутную матрицу невозможно.
4. Алгоритм программы, реализующий метод построения
маршрутной матрицы.
Алгоритм состоит из 6 функциональных блоков, выполняемых в порядке, который схематично изображен на рисунке 2 “Схема алгоритма”. Ниже приведено назначение и содержание всех 6-ти функциональных блоков. Алгоритм реализует описанный выше метод.
Блок 1.
Назначение: Ввод данных, необходимых для построения маршрутной матрицы.
Содержание: Ввод данных, конкретизирующих решаемую задачу (т. е. задачу построения маршрутной матрицы виртуальной СеМО (2.3) - (2.4)). Эти данные должны содержать число СМО в сети и матрицу смежности исходной концептуальной виртуальной СеМО, а также концептуальный вектор .
Блок 2.
Назначение: Задание начального приближения.
Содержание: Матрица формируется путем присвоения случайных значений элементам таких, что , где I - множество номеров элементов матрицы смежности, таких что
При этом необходимо соблюдать стохастичность матрицы, т. е. условия (2.4). Остальные элементы получают следующим образом:
( - элементы матрицы смежности).
Т. о. блок 2 реализует пункт 1 рассмотренного выше метода.
Блок 3. Реализует пункт 2 метода формирования маршрутной матрицы.
Назначение: Выбор направления, в котором будет осуществляться поиск экстремума.
Содержание: 3.1) Вычисление целевой функции текущей матрицы .
3.2) Выбор таких элементов и и величины , (положительной или отрицательной), что
После того как эти условия выполнены и элементы найдены переходят к условию 1:
1) Если , то передаются в качестве исходных данных в Блок 4 и управление передается Блоку 4.
2) Если 1) не выполняется, то текущая матрица запоминается как и управление переходит на Блок 5.
Подробно выбор элементов и описан выше в пункте 2 метода формирования матрицы .
Блок 4. Реализует пункт 3.
Назначение: Осуществляет движение в направлении выбранном Блоком 3 до тех пор пока не будет достигнута граница (условия (2.4)), либо вершина на этом направлении.
Содержание: Пока не будет достигнута граница, т. е. не перестанут выполняться условия:
( - выбраны Блоком 2)
Либо не будет достигнута вершина для текущего направления, т. е.
(*)
( (*) - условие достижения вершины в точке ). Повторяют рабочий шаг: присваивают значение .
Как только движение прекращается текущая матрица запоминается и управление передается в Блок 3.
Блок 5.
Назначение: Определить достигнут ли глобальный экстремум в точке , определенной Блоком 2. Т. е. достигнуто ли решение задачи (2.3) - (2.4).
Содержание: Проверяются условия 2:
Если ( - величина, определяющая точность, с которой ищется экстремум, содержится во входных данных), то делается вывод, что
- решение задачи (2.3) - (2.4);
Если , то если раз не был достигнут один и тот же минимум, управление передается в Блок 2 ( может быть задана в исходных данных).
В противном случае полагается, что решения задачи (2.3) - (2.4) достичь невозможно.
После проверки условия 2 управление передается в Блок 6.
Блок 6.
Назначение: Формирование выходных данных.
Содержание: Формируется сообщение, следующим образом:
Если решение найдено, то выходными данными является .
Если принято решение о невозможности достичь решения, то выходными данными будет сообщение о том, что решение не существует.
Рисунок 2. Структурная схема алгоритма реализующего
метод формирования маршрутной матрицы.
5. Назначение программы OPTIM и описание программы.
Программа OPTIM написана на языке Turbo Pascal. Программа предназначена для решения задачи формирования маршрутной матрицы виртуальной СеМО. Программа представляет собой реализацию алгоритма приведенного в предыдущей главе. Программа проста в использовании, требует незначительный объем оперативной памяти. Недостатком программы является недостаточно высокое быстродействие, как и у многих других программ, реализующих подобные методы оптимизации.
Маршрутные матрицы и матрицы смежности являются разряженными матрицами, т. е. матрицами, содержащими относительно малое число ненулевых элементов. Поэтому для исследования виртуальных СеМО большой размерности в программе OPTIM предусмотрено представление матриц смежности в виде вектора, содержащего номера столбцов, содержащих ненулевые элементы записанные в порядке возрастания номеров столбцов и строк. Номер последнего положительного элемента в строке берется со знаком “-”. Подобное представление матрицы смежности позволяет повысить скорость ввода исходных данных.
Программу можно условно разбить на функциональные блоки, выполненные в виде отдельных процедур и функций.
1. Ввод исходных данных. Реализует пункт 1 алгоритма. Выполнен в виде процедуры InputData.
Содержание: считывает исходные данные из файла OPT.DAT . Исходные данные выбираются в следующем порядке:
к - число ненулевых элементов матрицы смежности.
L - число СМО.
Svect - упакованная матрица смежности (вектор размерности к).
- концептуальный вектор (размерности L).
2. Задание начальной матрицы реализует Блок 2 алгоритма. Выполнен в виде процедур MatrSmez и TetaMatr. Процедура MatrSmez формирует матрицу смежности на основании вектора Svect. Процедура TetaMatr преобразует матрицу смежности в матрицу (подробно описано в алгоритме в Блоке 2).
3. Выбор направления спуска. Реализует Блок 3 алгоритма. Выполнен в виде процедуры IndLocate. Для работы использует функции target (teta) и stepish, вычисляющие значение целевой функции и степень полуисхода вершины соответственно.
4. Осуществляет движение в выбранном направлении. Реализует Блок 4 алгоритма, выполнена в виде процедуры Move.
5. Обработка результатов и формирования файла выходных данных. Реализует Блоки 5 и 6 алгоритма. Выполнен в виде процедуры OutputData.
Содержание: Обрабатывает результаты работы Блоков 2, 3, 4. Выходные данные формируются в виде выходного файла OPT. REZ
Выходной файл содержит либо полученную маршрутную матрицу виртуальной СеМО, либо сообщение о невозможности сформировать ее.
Текст программы помещен в приложении.
Заключение.
Целью данной работы являлась разработка метода решения задачи формирования маршрутных матриц виртуальной СеМО.
Были рассмотрены некоторые методы оптимизации и на их основе предложен метод формирования маршрутной матрицы.
Для него был разработан алгоритм и написана программа. Программа была испытана на контрольных примерах.
Так же был предложен метод получения общего решения поставленной задачи.
Список литературы.
Митрофанов Ю. И., Синтез сетей массового обслуживания.- Саратов: Изд-во ГуНЦ “Колледж”, 1995 -168 с.
Башарин Г. П., Бочаров П. П., Коган Я. А. Анализ очередей в вычислительных сетях. Теория и методы расчета. - М. Наука. Гл. ред. физ.-мат. лит., 1989 - 336 с.
Жиглявский А. А., Жилинскас А. Т. Методы поиска глобального экстремума. -М. Наука, Гл. ред. физ.-мат. лит., 1991 - 248 с.
Поляк Б. Т. Введение в оптимизацию. - М. Наука, 1983 - 384 с.
Зайченко Ю. П. Исследование операций. - Киев, Вища школа, 1975, 320 с.
Митрофанов Ю. И., Брагина И. Т., Тананко И. Е., Юдаева Н. В. Анализ и оптимизация сетей массового обслуживания. Программное обеспечение. - Саратов, Изд-во “Колледж”, 1995 - 144 с.
Похожие работы
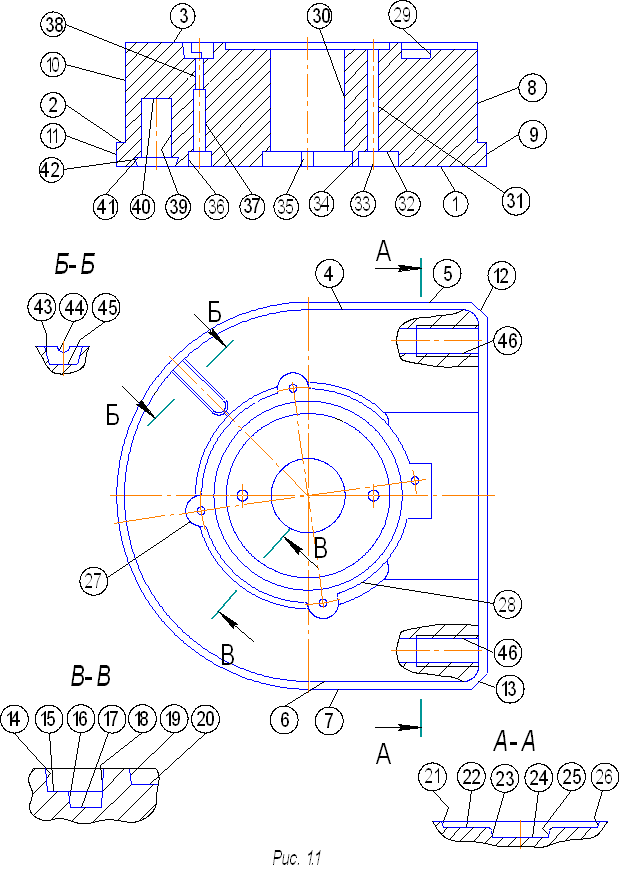
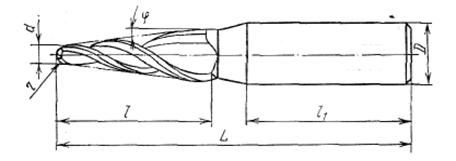
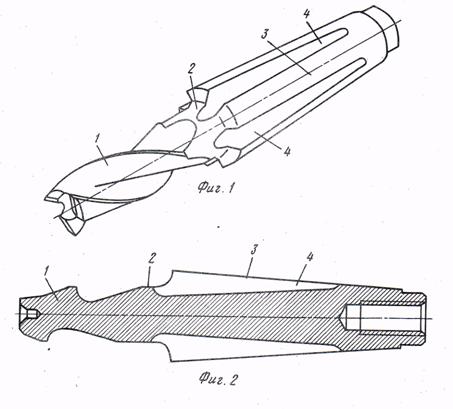
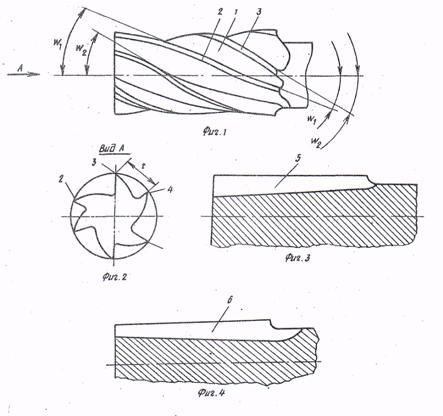
... 7 0,8 Сверление, зенкерование, развертывание. 34 12 12,5 Растачивание 36,37,46 11 12,5 Сверление Данные методы реализованы при разработке технологического маршрута изготовления матрицы. Разработка технологического маршрута изготовления матрицы При разработке маршрута в среднесерийном производстве придерживались следующих правил: 1.Технологические операции разрабатывали по принципу ...
... со строгими методами оптимизации образуют жесткую структуру, изменения которой осуществляются разработчиками или специальными лицами, администрирующими информационную компоненту и сопровождающими систему автоматизированного проектирования. Они не являются специалистами в данной предметной области. ЛОГИЧЕСКИЕ МЕТОДЫ ПРЕДСТАВЛЕНИЯ ЗНАНИЙ Предварительно остановимся на изложении некоторых понятий ...
0 комментариев