Навигация
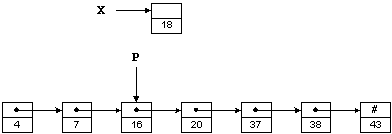
4 Задача о футболистах.
uses crt;
Const k=100;
Type mas=array[1..k]of Integer;
Var m,q:integer;
A,B:mas;
procedure Init(z:string); {инициализация исходных данных}
var i:integer;
f:text;
begin
Assign(f,z);
Reset(f);
ReadLn(f,m,q);
For i:=1 to m do
Read(f,A[i]);
ReadLn(f);
For i:=1 to q do
Read(f,B[i]);
Close(f);
end;
procedure Solve;
var i,j,t:integer;
D:mas;
begin
i:=1; j:=1; t:=1;
While (i<=m)and(j<=q)do {пока не вышли футболисты хотя бы из одного автобуса}
Begin
{сравниваем номера футболистов в разных автобусах, выходит в строй футболист с наименьшим номером}
If A[i]<=B[j] Then begin D[t]:=A[i]; Inc(i); end
Else begin D[t]:=B[j]; Inc(j); end;
Inc(t);
end;
{из одного автобуса вышли все футболисты, осталось выйти остальным}
While i<=m do begin D[t]:=A[i]; Inc(i); Inc(t); end;
While j<=q do begin D[t]:=B[j]; Inc(j); Inc(t); end;
For i:=1 to t-1 do Write(D[i],' ');
end;
begin
clrscr;
Init('A:socker.txt');
Solve;
readkey;
end.
5 Задача о семьях.
Uses crt;
Const MaxN=1000;
Var A:array[1..maxN]of byte;
N, cnt,i,j:integer;
Procedure Swap(var a,b:byte);
Var c:byte;
Begin
c:=a; a:=b; b:=c;
End;
Begin
Write(‘введите N’); readln(N);
Write(‘введите массив через пробел(0 – Петров, 1 - Иванов)’);
For i:=1 to N do read(A[i]);
i:=1; j:=N; cnt:=0;
While i<j do
If A[i]=1 then Inc(i) else
If A[j]=0 then Dec(j) else begin
Swap(A[i],A[j]);
Inc(i); dec(j);
Inc(cnt);
End;
writeLn(‘Число обменов - ’, cnt);
End.
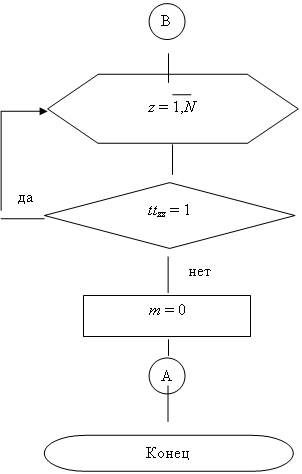
6 Метро.
uses crt;
const p=100;
Type mas=array[1..p,1..p]of 0..1;
var k,n:integer;
A:mas;
procedure Init(z:string); {инициализация данных}
var f:text;
i,j:integer;
begin
Assign(f,z);
Reset(f);
ReadLn(f,n);
For i:=1 to n do
begin
For j:=1 to n do
Read(f,A[i,j]);
ReadLn(f);
end;
Close(f);
end;
procedure Get(i:integer); {i – номер станции, из которой необходимо отправится}
var S,T:Set of 1..p;
j,l:integer;
begin
T:=[i];
Repeat
S:=T;
For l:=1 to n do
If l in S then {по строкам матрицы смежности А, принадлежащим множеству S}
For j:=1 to n do
If A[l,j]=1 Then T:=T+[j]; {смотрим если есть путь из данного пункта в пункт j, то добавляем номер пункта j в множество Т}
Until S=T;
For j:=1 to n do
If (j in T)and(i<>j) then Write(j,' '); {просматриваем содержится ли номер пункта j в множестве имеющих путь из пункта i}
end;
begin
clrscr;
Init('A:metro.txt');
readLn(k);
Get(k);
readkey;
end.
7 Роботы.
Program Robots;
Const max=50;
Type Sset=Set of 1..max;
Mas=array[1..max]of Sset;
Var A,B:Mas;
{A – матрица достижимостей, B[i] – какие роботы могут быть в i пункте}
SOne, STwo: SSet; {SOne – роботы, которые едут со скоростью 1, STwo – роботы, которые едут со скоростью 2}
N, M:integer; {N – число пунктов, M – число роботов}
Procedure Init; {инициализация входных данных}
Var K, i, FrP, ToP:integer;
Begin
FillChar(A,SizeOf(A),0);
Write(‘Число пунктов:’); ReadLn(N);
Write(‘Число дорог:’); ReadLn(K);
For i:=1 to K do begin
writeLn(‘Введите пункты, которые соединяет дорога №’, i);
ReadLn(FrP, ToP);
Include(A[FrP],ToP);
Include(A[ToP],FrP);
End;
Write(‘Число роботов:’); ReadLn(M);
For i:=1 to M do Begin
Write(‘Пункт, где находится робот №’,i,’:’); ReadLn(K);
Include(B[k],i);
Write(‘скорость робота №’,i,’:’);
ReadLn(k);
If K=1 then Include(SOne,i) Else Include(STwo,i);
End;
End;
Function ProvCanMet: Boolean;
Var i:integer;
Begin
i:=1;
While (i<=N)and(B[i]<>[1..M])do Inc(i);
ProvCanMet:=i<=N;
End;
Function InTwoNear: Boolean;
Var i,j:integer;
Begin
i:=1; j:=N+1;
while (i<N)and(j>N)do begin
j:=i+1;
while(j<=N)and Not((j in A[i])and(B[i]+B[j]=[1..M]))do Inc(j);
Inc(i);
End;
InTwoNear:=j<=N;
End;
Function AddIfCan(mode:integer; S:Sset):Boolean;
Var i,j:integer;
C:mas;
Begin
AddIfCan:=false; {S – множество роботов, которые едут}
If mode=0 then
For i:=1 to N do C[i]:=B[i]-S
Else C:=B;
For i:=1 to N do
For j:=1 to N do
If (i<>j)and(j in A[i])and(C[i]*B[j]*S<>B[j]*S) Then Begin
AddIfCan:=true;
C[i]:=C[i]+B[j]*S;
End;
B:=C;
End;
Function InTwoForC: byte;
Var i,j:integer;
Begin
i:=1; j:=N+1;
while (i<N)and(j>N)do begin
j:=i+1;
While (j<=N)and (not(j in A[i])or(B[i]+B[j]<>[1..m])or Not((SOne=[])or(STwo=[])or((B[i]*SOne=SOne)and(B[j]*STwo=STwo))or (B[j]*SOne=SOne)and(B[i]*STwo=STwo)))do Inc(j);
Inc(i);
End;
If j>N Then InTwoForC:=0 Else
If STwo=[] Then InTwoForC:=1 Else
If SOne=[] Then InTwoForC:=2 Else
InTwoForC:=3;
End;
Procedure SolveC;
Var time:integer;
FindS, IncS: Boolean;
ForMet: integer;
Begin
Time:=0;
IncS:=true;
ForMet:=InTwoForC;
FindS:=ProvCanMet;
While IncS and Not FindS and(time<=N*2)and(ForMet=0)do begin
Inc(time);
If Time Mod 2=0 then IncS:=AddIfCan(0,[1..m])
Else incS:=AddIfCan(0,STwo);
ForMet:=InTwoForC;
FindS:=ProvCanMet and(time mod 2=1);
End;
If Time>N*2 then WriteLn(‘Пункт В: Роботы не встретятся’)
Else begin
Write(‘Пункт В: Роботы встретятся через’);
If FindS Then Write(Time/2:0:3)
Else Case ForMet of
1: write((time+1)/2:0:3);
2: write(time/2+1/4:0:3);
3: write(time/2:0:3,’+1/’,(time mod 2+1)*3);
End;
WriteLn(‘Момент(а,ов) времени’);
End;
End;
Procedure SolveAB;
Var time:integer;
ForB, FindS, IncS: Boolean;
Old:mas;
Begin
Old:=B;
Time:=0;
IncS:=true; FindS:=ProvCanMet;
While IncS and Not FindS do begin
ForB:=InTwoNear;
Inc(time);
incS:=AddIfCan(1,[1..m]);
FindS:=ProvCanMet;
End;
If FindS Then begin
WriteLn(‘Пункт А:’,time,’момент(а,ов) времени’);
WriteLn(‘Пункт Б:’,time – Byte(ForB)*0.5:0:1,’момент(а,ов) времени’);
SolveC;
End
Else begin
WriteLn(‘Пункт А: Роботы не встретятся’);
writeLn(‘Пункт Б: Роботы не встретятся’);
writeLn(‘Пункт В: Роботы не встретятся’);
end;
B:=Old;
End;
Begin
Init;
SolveAB;
End.
Похожие работы
... подход к разработке эффективного алгоритма для решения любой задачи – изучить ее сущность. Довольно часто задачу можно сформулировать на языке теории множеств, относящейся к фундаментальным разделам математики. В этом случае алгоритм ее решения можно изложить в терминах основных операций над множествами. К таким задачам относятся и задачи информационного поиска, в которых решаются проблемы, ...
... ответ на этот вопрос положителен. Штрих Шеффера является отрицанием конъюнкции, стрелка Пирса – отрицание дизъюнкции, сумма Жегалкина – отрицание эквивалентности. М. Жегалкин (1869–1947) – российский математик и логик, один из основоположников современной математической логики. Чарльз Пирс (1839–1914) – американский логик, математик и естествоиспытатель. Основоположник семиотики, родоначальник ...
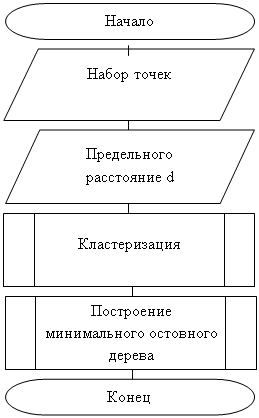
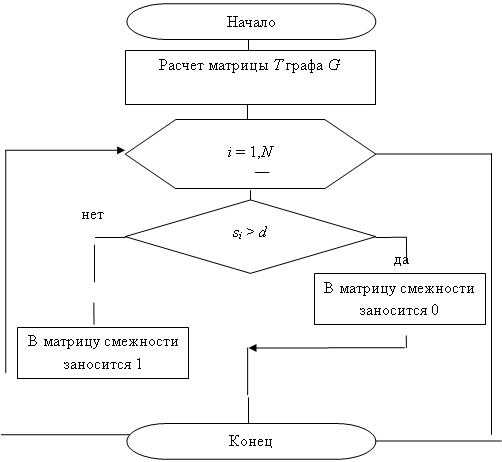
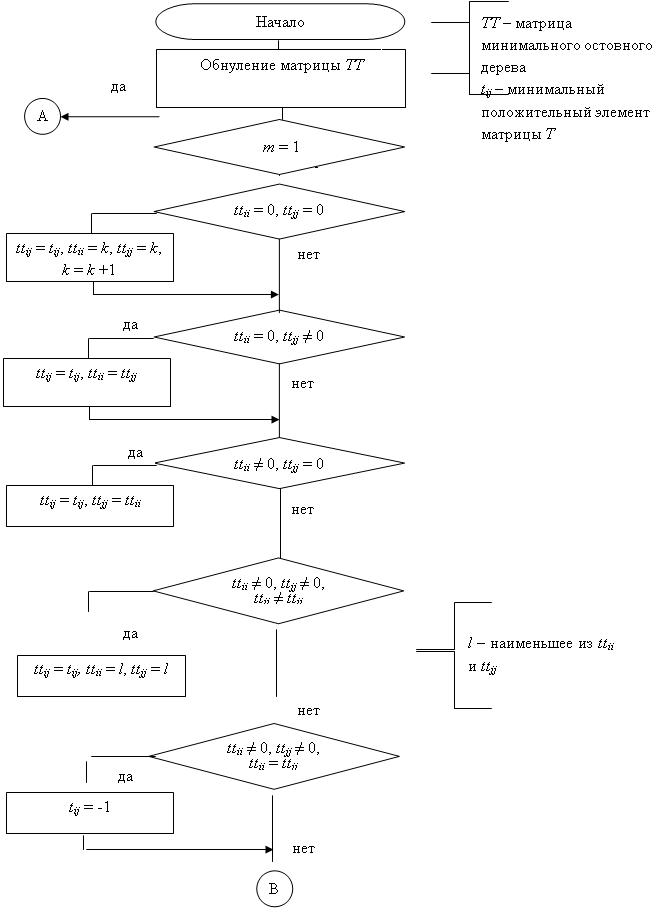
... все 1. Полученная матрица представлена на рисунке 7. Рисунок 7 – Тест первый (часть 3) 4.1 Тест второй. Результат выполнения алгоритма с 20-ю вершинами, заданными случайными координатами и предельным расстоянием равным 2,5 представлен на рисунке 8. Рисунок 8 – Тест второй (часть 1) На данном рисунке видно, что граф был разбит на 8 кластеров. Увеличим предельное расстояние до 3. ...
... . Целью дипломного проекта является разработка и исследование автоматической системы регулирования (АСР) асинхронного высоковольтного электропривода на базе автономного инвертора тока с трехфазным однообмоточным двигателем с детальной разработкой программы высокого уровня при различных законах управления. В ходе конкретизации из поставленной цели выделены следующие задачи. Провести анализ ...


0 комментариев