Навигация
8 Вожатый в лагере.
uses crt;
Const k=50;
Type mas=array[1..k]of integer;
var col:integer;
A:mas; {массив представляющий собой список возрастов детей}
procedure Init(z:string); {инициализация данных}
var i:integer;
f:text;
begin
Assign(f,z);
Reset(f);
i:=0;
While not EoLn(f) do
begin
Inc(i);
Read(f,A[i]);
end;
col:=i;
Close(f);
end;
procedure Print; {вывод списка на экран}
var i:integer;
begin
For i:=1 to col do
Write(A[i],' ');
end;
procedure Solve(m,t:integer);
var i,j,w,x:integer;
begin
If m>=t then exit;
i:=m; j:=t; x:=A[(m+t)div 2]; {x- барьерный элемент, т.е. возраст, относительно которого будет сортироваться список, i,j – нижний и верхний номер, рассматриваемой части списка}
While i<j do
If A[i]>x then Inc(i)else {смотрим элементы списка относительно
If A[j]<x then Dec(j)else барьерного элемента, пока не найдем из правой и
Begin левой части по элементу, которые стоят не на
w:=A[i]; A[i]:=A[j]; A[j]:=w; своем месте. Меняем их местами}
end;
Solve(m,j-1); Solve(i+1,t); {ищем далее барьерный элемент, сначала в правой
end; части списка, затем в левой}
begin
clrscr;
Init('A:alfa.txt');
Print;
WriteLn;
Solve(1,col);
Print;
readkey;
end.
9 Егерь.
Program Eger;
uses crt;
Const n=4;
var A,P,D:array[1..n,1..n]of Integer; {A – матрица смежности; D – массив кратчайших путей, где D[i,j] – минимальное время, которое потребуется, чтобы добраться из станции i до станции j; P – массив, элементами которого являются номера станций, которые будут составлять путь с минимальным временем}
k,m:integer; {начальная и конечная станции движения}
procedure Init(z:string); {инициализация данных}
var i,j:integer;
f:text;
begin
Assign(f,z);
Reset(f);
For i:=1 to n do
begin
For j:=1 to n do
Read(f,A[i,j]);
ReadLn(f);
end;
Close(f);
end;
Procedure Solve;
var i,j,k:integer;
begin
For i:=1 to n do
For j:=1 to n do
begin
D[i,j]:=A[i,j];
P[i,j]:=i;
end;
for k:=1 to n do begin
for i:=1 to n do
for j:=1 to n do
If D[i,j]>D[i,k]+D[k,j] then begin {определение пути с минимальным
D[i,j]:=D[i,k]+D[k,j]; временем}
P[i,j]:=k; {заносим номер станции, которая будет
end; предпоследней, посещенной напарником}
end;
end;
procedure Way(i,j:integer); {рекурсивная процедура, выводит
begin последовательность станций, которые посетит
If P[i,j]<>i then begin напарник, отталкиваясь от данных,
Way(i,P[i,j]); занесенных в массив P}
Write (P[i,j]:2,'->');
Way(P[i,j],j);
end
end;
begin
clrscr;
Init('A:eger.txt');
Solve;
Writeln('Введите из какой станции и в какую будем искать путь:');
Readln(k,m);
Write(k:2,'->');
Way(k,m);
WriteLn(m:2);
WriteLn(‘Время пути= ‘,D[k,m]);
readkey;
end.
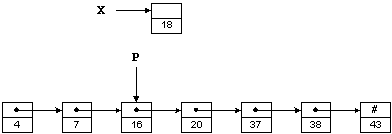
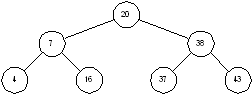
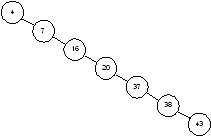
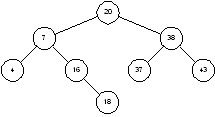
10 Игра «Найди друга».
uses crt;
Const n=20;
type mas=array[1..n]of Integer;
var A:mas;
X,b:integer;
procedure Init(z:string);
var i:integer;
f:text;
begin
Assign(f,z);
Reset(f);
For i:=1 to n do
Read(f,A[i]);
Close(f)
end;
procedure Print;
var i:integer;
begin
For i:=1 to n do
Write(A[i],' ');
end;
procedure Solve(i,j:integer;Var t:integer);
var m:integer;
begin
If i>j then Writeln('No')
else begin m:=(i+j)div 2;
Inc(b);
If A[m]<X then Solve(m+1,j,t)
else If A[m]>X then Solve(i,m-1,t)
else Write(b);
end;
end;
begin
clrscr;
Init('A:game.txt');
Print;
WriteLn;
ReadLn(x);
Solve(1,n,b);
readkey;
end.
Заключение.
В данном курсовом проекте мы разработали свой набор задач и критерии, по которым данный набор можно классифицировать. Несмотря на то, что разрабатывая критерии классификации, мы оперировали с конкретным набором задач, данная классификация может быть применима ко многим наборам задач. Единственное несоответствие, которое может произойти, это несоответствие по тематике. Таким образом, данная классификация достаточно универсальна и может иметь широкое практическое применение. При выполнении данного курсового проекта основные трудности пришлись на выбор литературы, так как по данной теме литературы немного и ее необходимо рассматривать с точки зрения методики преподавания информатики. В сборниках задач большое место отведено задачам, имеющим строгую формулировку, которую изменить на ситуативную достаточно сложно, так как задачи имеют маленькую практическую значимость в жизни.
Таким образом, цели поставленные при выполнении данного курсового проекта достигнуты.
Литература:
1) Б.Н. Иванов Дискретная математика. Алгоритмы и программы. Москва 2001г.
2) С.М. Окулов Программирование в алгоритмах. Москва 2002г.
3) Н.Вирт Алгоритмы и структуры данных. Москва «Мир» 1989г.
4) В.М. Кирюхин, А.В. Лапунов, С.М. Окулов Задачи по информатике. Международные олимпиады 1989-1996гг. Москва ABF 1996г.
5) С.М. Окулов, А.А. Пестов, О.А. Пестов Информатика в задачах. Киров 1998г.
6) Н.Вирт Систематическое программирование. Под ред. Ю.М. Баяковского. Москва «Мир» 1977г.
Похожие работы
... подход к разработке эффективного алгоритма для решения любой задачи – изучить ее сущность. Довольно часто задачу можно сформулировать на языке теории множеств, относящейся к фундаментальным разделам математики. В этом случае алгоритм ее решения можно изложить в терминах основных операций над множествами. К таким задачам относятся и задачи информационного поиска, в которых решаются проблемы, ...
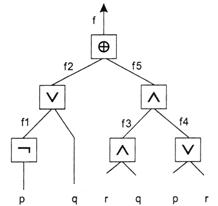
... ответ на этот вопрос положителен. Штрих Шеффера является отрицанием конъюнкции, стрелка Пирса – отрицание дизъюнкции, сумма Жегалкина – отрицание эквивалентности. М. Жегалкин (1869–1947) – российский математик и логик, один из основоположников современной математической логики. Чарльз Пирс (1839–1914) – американский логик, математик и естествоиспытатель. Основоположник семиотики, родоначальник ...
... все 1. Полученная матрица представлена на рисунке 7. Рисунок 7 – Тест первый (часть 3) 4.1 Тест второй. Результат выполнения алгоритма с 20-ю вершинами, заданными случайными координатами и предельным расстоянием равным 2,5 представлен на рисунке 8. Рисунок 8 – Тест второй (часть 1) На данном рисунке видно, что граф был разбит на 8 кластеров. Увеличим предельное расстояние до 3. ...
... . Целью дипломного проекта является разработка и исследование автоматической системы регулирования (АСР) асинхронного высоковольтного электропривода на базе автономного инвертора тока с трехфазным однообмоточным двигателем с детальной разработкой программы высокого уровня при различных законах управления. В ходе конкретизации из поставленной цели выделены следующие задачи. Провести анализ ...


0 комментариев