Навигация
АНАЛИЗ СФЕРИЧЕСКОГО ПЬЕЗОКЕРАМИЧЕСКОГО ПРЕОБРАЗОВАТЕЛЯ
САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ
МОРСКОЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
ФАКУЛЬТЕТ МОРСКОГО ПРИБОРОСТРОЕНИЯ
КАФЕДРА ФИЗИКИ
КУРСОВАЯ РАБОТА
АНАЛИЗ СФЕРИЧЕСКОГО ПЬЕЗОКЕРАМИЧЕСКОГО ПРЕОБРАЗОВАТЕЛЯ
ВЫПОЛНИЛ:
СТУДЕНТ ГРУППЫ 34РК1СУХАРЕВ Р.М.
ПРОВЕРИЛ:
ПУГАЧЕВ С.И.
САНКТ-ПЕТЕРБУРГ
ОСЕННИЙ СЕМЕСТР
1999г.
СОДЕРЖАНИЕ
| 1. Краткие сведения из теории | 3 |
| 2. Исходные данные | 7 |
| 3. Определение элементов эквивалентной электромеханической схемы, включая N, Ms, Rs, Rпэ, Rмп |
8 |
| 4. Нахождение конечных формул для КЭМС и КЭМСД и расчет их значений |
9 |
| 5. Определение частоты резонанса и антирезонанса |
9 |
| 6. Вычисление добротности электроакустического преобразователя в режиме излучения |
10 |
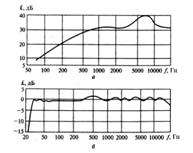
| 7. Расчет и построение частотных характеристик входной проводимости и входного сопротивления |
10 |
| 8. Список литературы | 16 |
1. КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
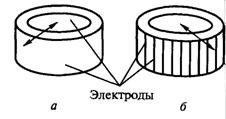
Пьезокерамический сферический преобразователь (Рис.1) представляет собой оболочку 2 (однородную или склеенную из двух полусфер), поляризованную по толщине, с электродами на внутренней и внешней поверхностях. Вывод от внутреннего электрода 3 проходит через отверстие и сальник 1, вклеенный в оболочке.
Рис. 1
Уравнение движения и эквивалентные параметры.
В качестве примера рассмотрим радиальные колебания ненагруженной тонкой однородной оболочки со средним радиусом а, поляризованный по толщине d, вызываемые действием симметричного возбуждения (механического или электрического).
Рис. 2
Направление его поляризации совпадает с осью z; оси x и y расположены в касательной плоскости (Рис.2). Вследствие эквипотенциальных сферических поверхностей E1=E2=0; D1=D2=0. Из-за отсутствия нагрузки упругие напряжения T3 равны нулю, а в силу механической однородности равны нулю и все сдвиговые напряжения. В силу симметрии следует равенство напряжений T1=T2=Tc, радиальных смещений x1=x2xС и значения модуля гибкости, равное SC=0,5(S11+S12). Заменив поверхность элемента квадратом (ввиду его малости) со стороной l, запишем относительное изменение площади квадрата при деформации его сторон на Dl:
Очевидно, относительной деформации площади поверхности сферы соответствует радиальная деформация , определяемая, по закону Гука, выражением
.
Аналогия для индукции:
.
Исходя из условий постоянства T и E, запишем уравнение пьезоэффекта:
; . (1)
Решая задачу о колебаниях пьезокерамической тонкой сферической оболочки получим уравнения движения сферического элемента
, (2)
где
(3)
представляет собой собственную частоту ненагруженной сферы.
Проводимость равна
, (4)
где энергетический коэффициент связи сферы определяется формулой
. (5)
Из (4) находим частоты резонанса и антирезонанса:
; . (6)
Выражение (4) приведем к виду:
.
Отсюда эквивалентные механические и приведенные к электрической схеме параметры, коэффициент электромеханической трансформации и электрическая емкость сферической оболочки равны:
; ;
Электромеханическая схема нагруженной сферы. Учесть нагрузку преобразователя можно включением сопротивления излучения , последовательно с элементами механической стороны схемы (Рис. 3). Напряжение на выходе приемника и, следовательно, его чувствительность будут определяться дифрагированной волной, которая зависит от амплитудно-фазовых соотношений между падающей и рассеянной волнами в месте расположения приемника. Коэффициент дифракции сферы kД, т.е. отношение действующей на нее силы к силе в свободном поле, равен , где p- звуковое давление в падающей волне, ka- волновой аргумент для окружающей сферу среды.
Приведем формулу чувствительности сферического приемника:
,
где ;
;
.
Колебания реальной оболочки не будут пульсирующими из-за наличия отверстия в оболочке (для вывода проводника и технологической обработки) и неоднородности материала и толщины, не будут так же выполняться и сформулированные граничные условия.
2. ИСХОДНЫЕ ДАННЫЕ
ВАРИАНТ С-41
| Материал | ТБК-3 | ||
| r, | 5400 |
| ||
| , | 8,3 × 10-12 |
| ||
| , | -2,45 × 10-12 |
| ||
| n=- | 0,2952 |
| ||
| , | 17,1 × 1010 |
| ||
| d31, | -49 × 10-12 |
| ||
| e33, | 12,5 |
| ||
| 1160 |
| |||
| 950 |
| |||
| tgd33 | 0,013 |
| ||
| , | 10,26 × 10-9 |
| ||
| , | 8,4 × 10-9 |
| ||
a=0,01 м – радиус сферы
м – толщина сферы
a=0,94
b=0,25
hАМ=0,7 – КПД акустомеханический
e0=8,85×10-12
(rc)В=1,545×106
3. ОПРЕДЕЛЕНИЕ ЭЛЕМЕНТОВ ЭКВИВАЛЕНТНОЙ ЭЛЕКТРОМЕХАНИЧЕСКОЙ СХЕМЫ, ВКЛЮЧАЯ N, Ms, Rs, Rпэ, Rмп
Электромеханическая схема цилиндрического излучателя:
Рис. 3
коэффициент электромеханической трансформации:
N=-2,105
присоединенная масса излучателя:
MS=4,851×10-5 кг
сопротивление излучения:
RS=2,31×103
активное сопротивление (сопротивление электрических потерь):
RПЭ=1,439×103 Ом
СS=4,222×10-9 Ф
сопротивление механических потерь:
RМП=989,907
4. НАХОЖДЕНИЕ КОНЕЧНЫХ ФОРМУЛ ДЛЯ КЭМС И КЭМСД
И РАСЧЕТ ИХ ЗНАЧЕНИЙ
Представим эквивалентную схему емкостного ЭАП для низких частот: Рис. 4
статическая податливость ЭАП:
C0=9,31×10-11 Ф
электрическая емкость свободного преобразователя:
CT=4,635×10-9 Ф
КЭМС=0,089 ; КЭМСД=0,08
5. ОПРЕДЕЛЕНИЕ ЧАСТОТЫ РЕЗОНАНСА И АНТИРЕЗОНАНСА:
wр=1,265×107
wА=1,318×107
6. ВЫЧИСЛЕНИЕ ДОБРОТНОСТИ ЭЛЕКТРОАКУСТИЧЕСКОГО ПРЕОБРАЗОВАТЕЛЯ В РЕЖИМЕ ИЗЛУЧЕНИЯ
Qm=65,201
эквивалентная масса:
MЭ=0,017 кг
Похожие работы
... 5.1 Назначение и логическая структура Данная программа реализована в интегрированной среде программирования Delphi и реализует модель системы идентификации плоской детали произвольной формы акустической локационной системой. Главная форма представляет собой окно, в котором отображается процесс идентификации детали, после чего программой определяется и выводится на экран количество отличий ...
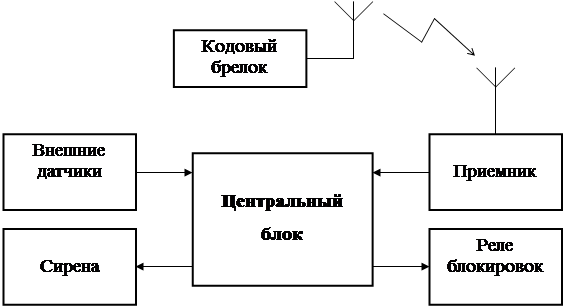
... , элементы питания – 2400 мм2) высота пульта управления с учётом ширины корпуса будет равна 10 мм. 7. ТЕХНИКО-ЭКОНОМИЧЕСКОЕ ОБОСНОВАНИЕ 7.1 Характеристика проекта Проектируемая система представляет собой систему охранной сигнализации автомобилей. В разрабатываемой системе будут реализованы функции, как автономной охраны, так и централизованной. Так, например, она будет в режиме «Тревога» ...


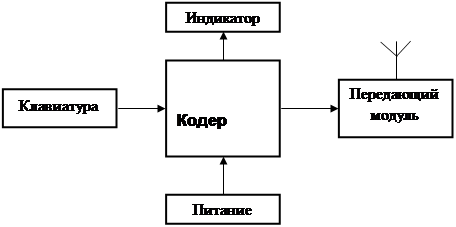

0 комментариев