Работа
биполярного
транзистора
в импульсном
режиме
Математическая
модель биполярного
транзистора
Измерение
параметров
биполярного
транзистора
Применение
биполярных
транзисторов
в электронных
схемах
Введение
Анализ
процессов в
биполярном
транзисторе
Статические
характеристики
биполярного
транзистора
Анализ
эквивалентных
схем биполярного
транзистора
Навигация
Математическая модель биполярного транзистора
Анализ и моделирование биполярных транзисторов
82277
знаков
1
таблица
0
изображений
10. Математическая модель биполярного транзистора.
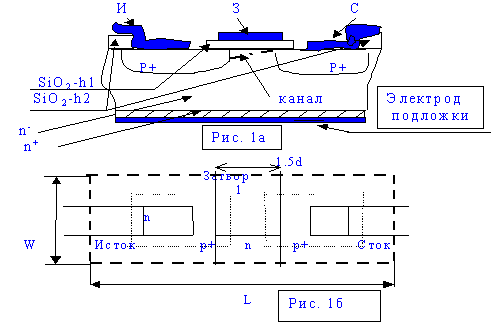
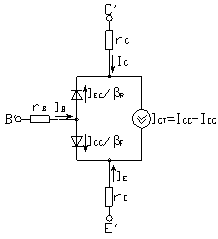
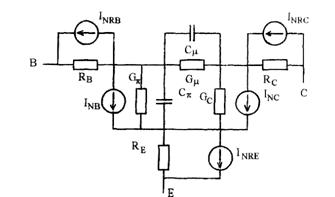
Общая эквивалентная схема транзистора, используемая при получении математической модели, показана на рис.10-1. Каждый p-n-переход представлен в виде диода, а их взаимодействие отражено генераторами токов. Если эмиттерный p-n-переход открыт, то в цепи коллектора будет протекать ток, несколько меньший эмиттерного (из-за процесса рекомбинации в базе). Он обеспечивается генератором тока . Индекс N означает нормальное включение. Так как в общем случае возможно и инверсное включение транзистора, при котором коллекторный p-n-переход открыт, а эмиттерный смещен в обратном направлении и прямому коллекторному току соответствует эмиттерный ток , в эквивалентную схему введен второй генератор тока , где - коэффициент передачи коллекторного тока.
Таким образом, токи эмиттера и коллектора в общем случае содержат две составляющие: инжектируемую ( или ) и собираемую ( или ):
, (10.1)
Эмиттерный и коллекторный p-n -переходы транзистора аналогичны p-n -переходу диода. При раздельном подключении напряжения к каждому переходу их вольтамперная характеристика определяется так же, как и в случае диода. Однако если к одному из p-n -переходов приложить напряжение, а выводы другого p-n -перехода замкнуть между собой накоротко, то ток, протекающий через p-n -переход, к которому приложено напряжение, увеличится из-за изменения распределения неосновных носителей заряда в базе. Тогда:
, (10.2)
где - тепловой ток эмиттерного p-n -перехода, измеренный при замкнутых накоротко выводах базы и коллектора; - тепловой ток коллекторного p-n -перехода, измеренный при замкнутых накоротко выводах базы и эмиттера.
Рис. 10-1. Эквивалентная схема идеализированного транзистора
Связь между тепловыми токами p-n -переходов ,включенных раздельно, И тепловыми токами , получим из (10.1 и 10.2). Пусть . Тогда . При . Подставив эти выражения в (10.1), для тока коллектора получим .
Соответственно для имеем
Токи коллектора и эмиттера с учетом (10.2) примут вид
(10.3)
На основании закона Кирхгофа ток базы
(10.4)
При использовании (10.1)-(10.4) следует помнить, что в полупроводниковых транзисторах в самом общем случае справедливо равенство
(10.5)
Решив уравнения (10.3) относительно , получим
(10.6)
Это уравнение описывает выходные характеристики транзистора.
Уравнения (10.3), решенные относительно , дают выражение, характеризующее идеализированные входные характеристики транзистора:
(10.7)
В реальном транзисторе кроме тепловых токов через переходы протекают токи генерации — рекомбинации, канальные токи и токи утечки. Поэтому ,, , как правило, неизвестны. В технических условиях на транзисторы обычно приводят значения обратных токов p-n-переходов ,. определенные как ток соответствующего перехода при неподключенном выводе другого перехода.
Если p-n-переход смещен в обратном направлении, то вместо теплового тока можно подставлять значение обратного тока, т. е. считать, что и . В первом приближении это можно делать и при прямом смещении p-n-перехода. При этом для кремниевых транзисторов вместо следует подставлять , где коэффициент m учитывает влияние токов реального перехода (m = 2 - 4). С учетом этого уравнения (10.3), (10.5) часто записывают в другом виде, который более удобен для расчета цепей с реальными транзисторами:
(10.8)
(10.9)
(10.10)
где .
Различают три основных режима работы биполярного транзистора: активный, отсечки, насыщения.
В активном режиме один из переходов биполярного транзистора смещен в прямом направлении приложенным к нему внешним напряжением, а другой - в обратном направлении. Соответственно в нормальном активном режиме в прямом направлении смещен эмиттерный переход, и в (10.3), (10.8) напряжение имеет знак «+». Коллекторный переход смещен в обратном направлении, и напряжение в (10.3) имеет знак « - ». При инверсном включении в уравнения (10.3), (10.8) следует подставлять противоположные полярности напряжений , . При этом различия между инверсным и активным режимами носят только количественный характер.
Для активного режима, когда и (10.6) запишем в виде .
Учитывая, что обычно и , уравнение (10.7) можно упростить:
(10.11)
Таким образом, в идеализированном транзисторе ток коллектора и напряжение эмиттер-база при определенном значении тока не зависят от напряжения, приложенного к коллекторному переходу. В действительности изменение напряжения меняет ширину базы из-за изменения размеров коллекторного перехода и соответственно изменяет градиент концентрации неосновных носителей заряда. Так, с увеличением ширина базы уменьшается, градиент концентрации дырок в базе и ток увеличиваются. Кроме этого, уменьшается вероятность рекомбинации дырок и увеличивается коэффициент . Для учета этого эффекта, который наиболее сильно проявляется при работе в активном режиме, в выражение (10.11) добавляют дополнительное слагаемое
(10.12)
- дифференциальное сопротивление запертого коллекторного p-n-перехода.
Влияние напряжения на ток оценивается с помощью коэффициента обратной связи по напряжению
,
который показывает, во сколько раз следует изменять напряжение для получения такого же изменения тока , какое дает изменение напряжения . Знак минус означает, что для обеспечения = const приращения напряжений должны иметь противоположную полярность. Коэффициент достаточно мал (), поэтому при практических расчетах влиянием коллекторного напряжения на эмиттерное часто пренебрегают.
В режиме глубокой отсечки оба перехода транзистора смещены в обратном направлении с помощью внешних напряжений. Значения их модулей должны превышать . Если модули обратных напряжений приложенных к переходам транзистора окажутся меньше , то транзистор также будет находиться в области отсечки. Однако токи его электродов окажутся больше, чем в области глубокой отсечки.
Учитывая, что напряжения и имеют знак минус, и считая, что и , выражение (10.9) запишем в виде
(10.13)
Подставив в (10.13) значение , найденное из (10.8), и раскрыв значение коэффициента А, получим
(10.14)
что , а , то выражения (10.14) существенно упростятся и примут вид
(10.15)
где ;
Из (10.15) видно, что в режиме глубокой отсечки ток коллектора имеет минимальное значение, равное току единичного p-n-перехода, смещенного в обратном направлении. Ток эмиттера имеет противоположный знак и значительно меньше тока коллектора, так как . Поэтому во многих случаях его считают равным нулю: .
Ток базы в режиме глубокой отсечки приблизительно равен току коллектора:
(10.15)
Режим глубокой отсечки характеризует запертое состояние
транзистора, в котором его сопротивление максимально, а токи
электродов минимальны. Он широко используется в импульсных устройствах, где биполярный транзистор выполняет функции электронного ключа.
При режиме насыщения оба p-n-перехода транзистора с помощью приложенных внешних напряжений смещены в прямом направлении. При этом падение напряжения на транзисторе () минимально и оценивается десятками милливольт. Режим насыщения возникает тогда, когда ток коллектора транзистора ограничен параметрами внешнего источника энергии и при данной схеме включения не может превысить какое-то значение . В то же время параметры источника внешнего сигнала взяты такими, что ток эмиттера существенно больше максимального значения тока в коллекторной цепи: .
Тогда коллекторный переход оказывается открытым, падение напряжения на транзисторе—минимальным и не зависящим от тока эмиттера. Его значение для нормального включения при малом токе () равно
(10.16)
Для инверсного включения
(10.16)
В режиме насыщения уравнение (10.12) теряет свою справедливость. Из сказанного ясно, что, для того чтобы транзистор из активного режима перешел в режим насыщения, необходимо увеличить ток эмиттера (при нормальном включении) так, чтобы начало выполняться условие . Причем значение тока , при котором начинается этот режим, зависит от тока , определяемого параметрами внешней цепи, в которую включен транзистор.
44
Похожие работы
... САПРа затраты машинного времени на определение нелинейных функций, описывающих различные полупроводниковые приборы составляют значительную часть общих затрат времени. 1. Проблема математического моделирования биполярных транзисторов Под моделированием понимается описание электрических свойств полупроводникового устройства или группы таких устройств, связанных между собой, с помощью ...
... к модификации межэлектродных ёмкостей, а также режим работы транзистора – режимы большого или малого тока коллектора (проявление эффекта Кирка). Необходимо и достаточно параметры математической модели биполярных транзисторов описываются 8-ю характеристиками: Зависимостью напряжения на переходе эмиттер-база Uбэ в режиме насыщения от тока коллектора (желательно иметь диапазон изменения тока ...
... параметров модели транзистора, зависимости этих параметров от температуры и конструкции, рассмотрены методы экстракции параметров модели из экспериментальных характеристик. Анализ PSpice модели БТ показал, что наряду с достоинствами этой модели есть и существенные недостатки. В целом модель биполярного транзистора в PSpice может с высокой точностью и в широком диапазоне напряжений, токов и ...
... генератора тока базы в прямом (23) в инверсном (24) включениях; - проводимость GC – проводимость генератора тока коллектора в прямом и инверсных включениях (25) Шумовая модель биполярного транзистора При анализе частотных зависимостей передаточных характеристик в рамках анализа по переменному току линейных (усилительных) ИС может проводиться и анализ шумовых ...
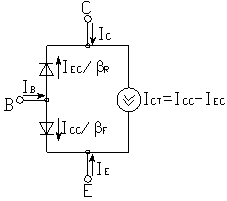
0 комментариев