Навигация
2 АНАЛИЗ ФОРМЫ СИГНАЛА
2.1 Математическая модель видеосигнала и его спектр
Выражение для определения полиномов Чебышева (третьего рода) и полином Чебышева третьего порядка представлены формулами (2.1.1) и (2.1.2) соответственно.
|
|
T3(x) = (4*x3-3*x)
Математическая модель видеосигнала представляет собой промасштабированный полином Чебышева третьего порядка. Масштабирование осуществляется путем замены переменной x на новую переменную kt. Коэффициент k выбирается так, чтобы выполнялось условие kt=1 при t=T и kt=-1 при t=-T (так как функция Чебышева ортогональна при -1<x<1). Параметр Т задан и , значит k=1/T.
После масштабирования полином Чебышева примет вид, представленный в формуле (2.1.3).
|
T3(x) = 4*(t/T)3-3*(t/T)
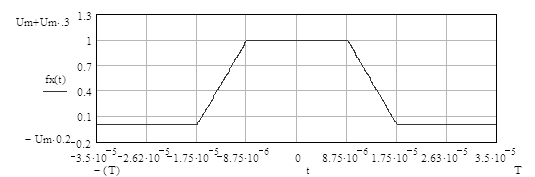
Математическая модель видеосигнала будет описываться функцией, представленной в формуле (2.1.4) на промежутке tÎ[-T, T]. Окончательная модель видеосигнала имеет вид:
|
Так как большинство расчётов будет производиться преимущественно численными методами с помощью специализированного программного обеспечения, то математическую модель видеосигнала можно записать с помощью единичной функции. Это приведено в формуле (2.1.5).
|
Графическое изображение модели видеосигнала приведено в приложении А на рисунке А.1
Спектральную плотность видеосигнала находится с помощью прямого преобразования Фурье математической модели видеосигнала:
|
где - оператор Фурье;
- спектральная плотность видеосигнала, ;
- частота, .
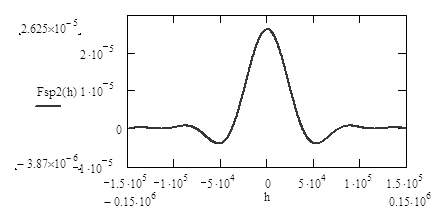
Спектральная плотность видеосигнала находится по формуле (2.1.7).
|
Графики спектральной плотности для заданного видеосигнала изображён в приложении А на рисунке А.2
2.2 Математические модели сигналов, соответствующих заданному видео сигналу, и их спектры
2.2.1 Периодическая последовательность видеосигналов
Математическая модель периодической последовательности видеосигналов, изображенная в приложении А на рисунке А.3, вычисляется по формуле (2.2.1.1)
|
где Sp(t) - математическая модель периодической последовательности видеосигналов;
s(t) – математическая модель видеосигнала;
- период повторения видеосигналов.
График периодической последовательности видеосигналов изображён в приложении А на рисунке А.3
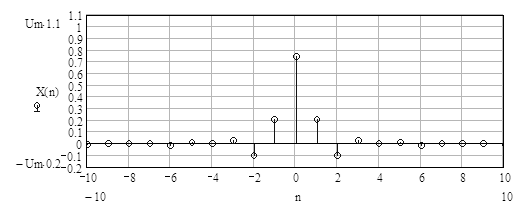
Спектр периодической последовательности видеосигналов вычисляется по формуле (2.2.1.2)
|
|
где ;
.
График спектральной плотности периодической последовательности видеосигналов изображён в приложении А на рисунке А.4
2.2.2. Радиосигнал с огибающей в форме видеосигнала.
Выражение для радиосигнала с огибающей в форме видеосигнала представлено в формуле (2.2.2.1).
|
- начальная фаза колебания;
- частота колебания.
Частота радиосигнала совпадает с резонансной частотой колебательного звена, которая определяется по формуле (2.2.2.2).
|
Значения L и С в формуле (2.2.2.2) берутся из задания на курсовую работу. В итоге имеем рад*МГц.
Графическое изображение радиосигнала приведено в приложении А на рисунке А.5
Спектральная плотность радиосигнала определяется по формуле (2.2.2.3)
|
График модуля спектральной плотности радиосигнала приведён в приложении А на рисунке А.6
Похожие работы
... тем шире спектр и наоборот. 2) Огибающая спектра периодического сигнала имеет форму спектральной плотности одиночного сигнала. 3) Спектр амплитудно-модулированного радиосигнала представляет собой фактически спектр модулирующего видеосигнала, смещенный по оси частот на (f0)ω0. 4) Спектр дискретного сигнала представляет собой сумму спектров видеосигнала смещенных друг относительно друга на ...
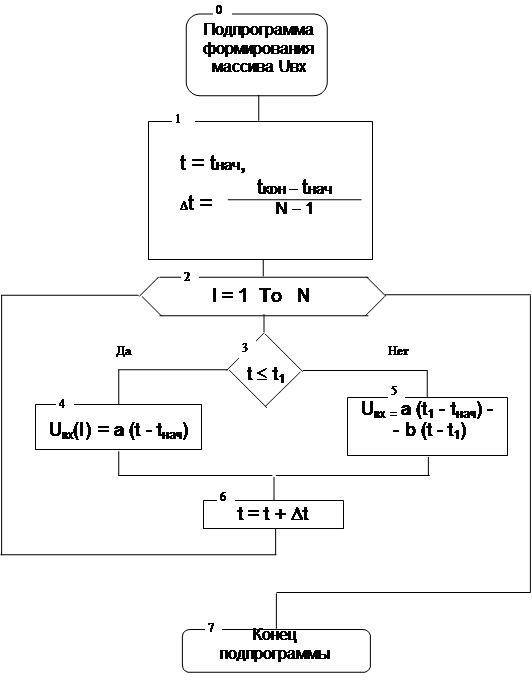
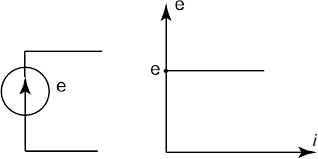
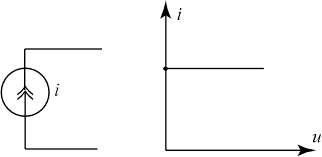
... . 1.2. Если в данный момент времени , это означает, что направление тока в проводнике совпадает с направлением, указанным стрелкой, т. е. положительные заряды перемещаются в направлении стрелки. В теории электрических цепей допускается возможность однозначной, не зависящей от выбора пути, оценки электрических напряжений меду любыми двумя зажимами исследуемой электрической цепи. Это позволяет ...
... В данной работе решаются задачи машинного анализа электрических цепей. В курсовом проекте необходимо для заданной электрической цепи по известному входному сигналу UВХ(t) построить выходной сигнал UВЫХ(t) , а затем определить некоторые его характеристики W. Характеристика W вычисляется с погрешностью не более 0.1. Погрешность вычисления величины W зависит от количества расчетных точек N, для ...
... цепи для передачи и преобразования электрической энергии и цепи для передачи и преобразования информации. Основные понятия и элементы линейных пассивных электрических цепей Электрический ток и напряжение - основные величины, характеризующие состояние электрических цепей. Электрический ток в проводнике есть упорядоченное перемещение электрических зарядов. Ток оценивают интенсивностью или ...
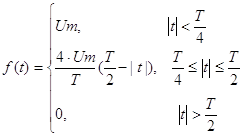




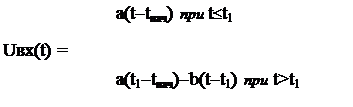
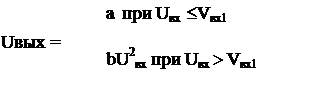


0 комментариев