Навигация
Многоканальные сигнатурные анализаторы
2.3. Многоканальные сигнатурные анализаторы.
Проблема анализа многовыходных цифровых схем и процесс их тестирования заключается в определении возникновения неисправности схемы по её выходным реакциям. Отличительной особенностью подобного анализа является необходимость исследования достаточно большого количества выходных реакций схемы (число их может достигать нескольких сотен). Поэтому использование традиционных методов компактного тестирования, применяемых для одновыходных цифровых схем, в данном случае не позволяет получить желаемого эффекта.[5] Действительно, попытка провести анализ n - выходной цифровой схемы одноканальным СА приводит к увеличению в n раз времени, необходимого для анализа схемы, или оборудования, требуемого для реализации n сигнатурных анализаторов. При этом остаётся открытым вопрос о разрядности сигнатуры, которая также может увеличиться в n раз. Поэтому на практике чаще всего используют специальные методы и приёмы. Наиболее часто применяемым из них является метод, основанный на преобразовании n выходных последовательностей длиной в одну последовательность по выражению:
(2.3.1)
Практическая реализация этого метода может быть выполнена как процедура сжатия в пространстве или во времени. В том и другом случае реализуется идея получения компактных оценок, характерная для методов компактного тестирования.
Как показано в [6] эффективность алгоритма сжатия информации, реализующего соотношение (2.3.1) определяется как:
(2.3.2)
где m - кратность ошибки, причём для нечётных значений m (- это вероятность необнаружения ошибки кратности m).
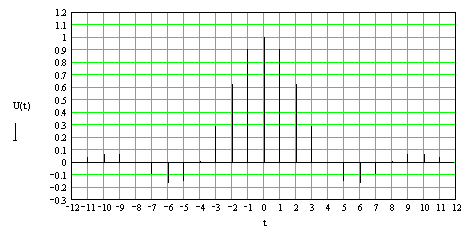
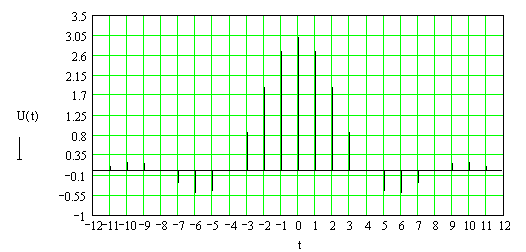
Для оценки вида распределения вероятностей рассмотрим конкретный пример n=3 – выходной цифровой схемы, длина выходных реакций которой составляет 21. В результате преобразования трех исходных последовательностей в последовательность , некоторые их ошибки станут необнаруживаемыми и будут оцениваться выражением:
(2.3.3)
которое справедливо для .
Ограничиваясь , определяем согласно (2.3.3) .
Анализ полученных численных значений вероятностей , а также общего выражения (2.3.2) показывает неравномерность закона их распределения, что свидетельствует о достаточно невысокой эффективности рассматриваемого алгоритма сжатия. Кроме того, необходимо отметить большую размерность результата сжатия, которая равна длине выходных реакций схемы. Поэтому на практике чаще всего используется компромиссное решение, заключающееся в двухступенчатом преобразовании выходных реакций n – выходной цифровой схемы. Первоначально n выходных последовательностей длиной преобразуются в последовательность по выражению (2.3.1). Далее сформированная таким образом последовательность снимается в m – разрядную сигнатуру (рис. 2.4)
|
Y2(k)
Y0(k) S(x)
Yn(k)
Рис. 2.4. Многоканальный сигнатурный анализатор.
Эффективность данного преобразования согласно [6] при m=4 определится как
(2.3.4)
где m – старшая степень порождающего полинома.
Эта формула справедлива, когда .
Наиболее распространенная структура многоканального сигнатурного анализатора для исследования многовыходных цифровых схем, которая построена на базе порождающего полинома , приведена на рис. 2.5.
j1(k) j2(k) j3(k) j4(k)
M2 M2 M2 M2
D TT D TT D TT D TT
C C C C
a1(k) a2(k) a3(k) a4(k)
ТАКТ
M2
Рис. 2.5. Четырехканальный сигнатурный анализатор.
Она используется для анализа выходных реакций четырехвыходных цифровых схем. При этом конечное значение кода является результирующим значением сигнатуры S(y), представляющей собой компактную оценку сжатия четырех последовательностей
Можно показать, что схема, приведённая на рис.2.5, эквивалентна относительно конечного результата простейшей сигнатуры двухступенчатого сжатия информации (рис. 2.4). А это значит, что в обоих случаях для оценки эффективности можно применять формулу (2.3.3). Оба подхода получения сигнатур отличаются неравномерностью закона распределения вероятностей необнаружения ошибки кратности m, а, следовательно, невысокой эффективностью. Кроме того, сигнатура многоканального сигнатурного анализатора (МСА), а также размерность сигнатуры S(y) однозначно определяется количеством выходов n исследуемой схемы. Поэтому с увеличением n сложность устройства сжатия и количество бит, используемых для представления сигнатуры S(y), принимает практически недопустимые размеры. Попытка использовать идею каскадирования многоканальных сигнатурных анализаторов позволяет уменьшить размерность результирующей сигнатуры, однако в этом случае оказывается сложным оценить достоверность такого анализатора [6], которая будет зависеть от организации взаимосвязи МСА и их конкретной реализации.
2.4.Многоканальный сигнатурный анализатор использованный в данной работе.
Предположим, что рассмотренный одноканальный анализатор используется для анализа цифрового узла, имеющего каналов, причём выходных последовательностей в данном случае преобразуются в одну последовательность вида
где - значение двоичного символа на -м выходе цифрового узла в -й такт его работы, а тактовая частота работы анализатора в раз выше частоты синхронизации исследуемого узла. При этом в каждый такт работы анализатора на его вход последовательно, начиная с первого выхода, поступают значения . Функционирование одноканального анализатора в многоканальном режиме, когда количество каналов равняется , описывается системой уравнений
где численное значение коэффициентов определяется на основании следующей системы уравнений
Коэффициенты определятся следующим образом:
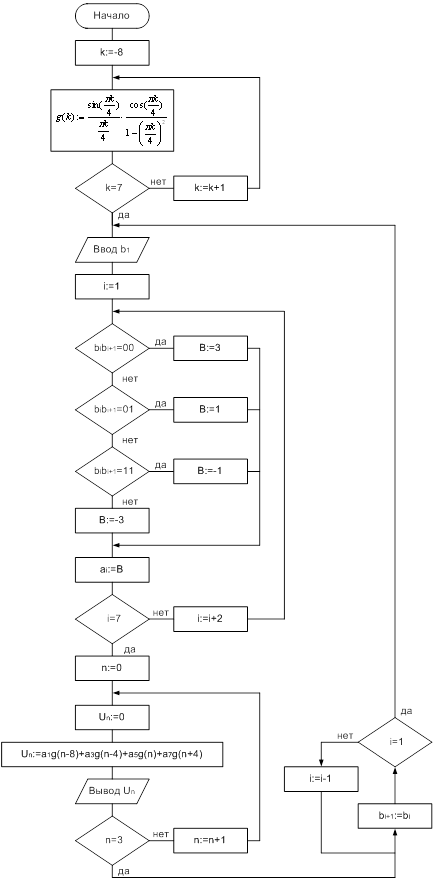
2.5. Алгоритм построения многоканального сигнатурного анализатора.
Для заданных значений и , где определяет достоверность диагностирования, алгоритм построения многоканального сигнатурного анализатора состоит из следующих этапов.
1. Вычисляются постоянные коэффициенты
где
2. Определяются коэффициенты причём значения коэффициентов вычисляются на основании соответствующей системы уравнений, а значения остальных коэффициентов определяются согласно выражению
3. Строится функциональная схема многоканального сигнатурного анализатора на основании полученной системы уравнений
При этом используются результаты этапов 1 и 2, позволяющих однозначно определить топологию связей многовходовых сумматоров по модулю два, на выходах которых формируются значения .
Похожие работы
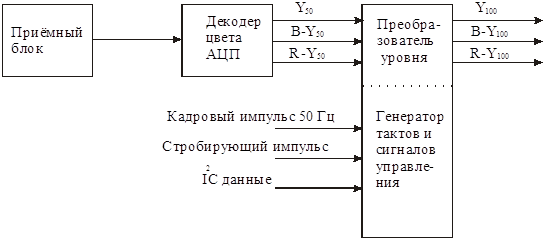
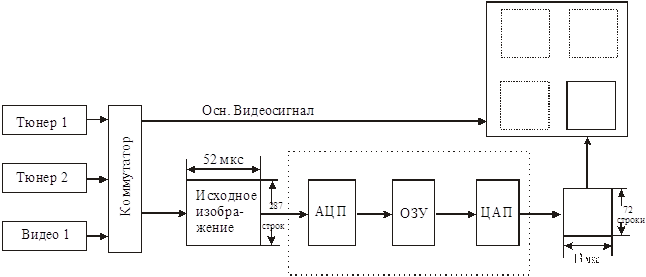
... Студент группы 220352 Чернышёв Д. А. Справка— отчет о патентном и научно- техническом исследовании Тема выпускной квалификационной работы: телевизионный приёмник с цифровой обработкой сигналов. Начало поиска 2. 02. 99. Окончание поиска 25.03.99 Предмет поиска Страна, Индекс (МКИ, НКИ) № ...
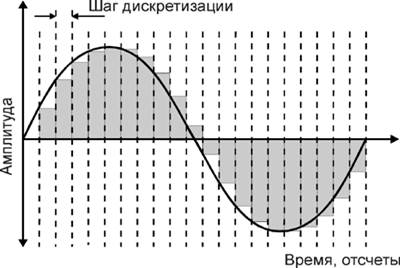
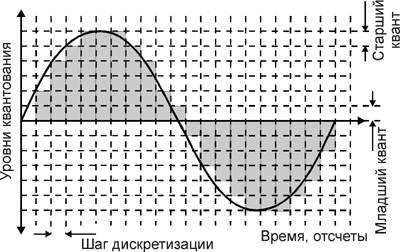
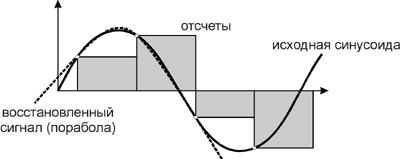
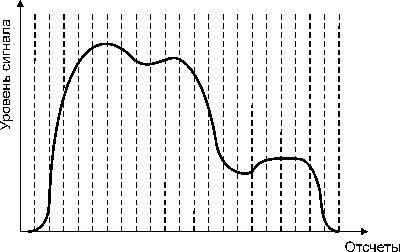
... 1 – «-» Причем 1-ый разряд слева – знаковый разряд. 16 14 12 10 8 6 4 2 Т 2Т 2. Связи между аналоговыми и дискретными сигналами. При обработке сигнала на ЭВМ необходимо в максимальной степени, чтобы дискретный или цифровой сигнал содержал все признаки аналогового сигнала. При дискретизации возможна потеря информации, которая ...
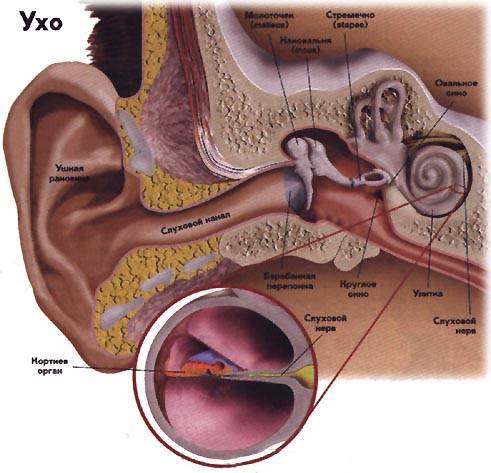
... примерно 6%. В общем, в районе 1 - 4 кГц чувствительность уха по всем параметрам максимальна, и составляет не так уж и много, если брать не логарифмированные значения, с которыми приходится работать цифровой технике. Примите на заметку - многое из того, что происходит в цифровой обработке звука, может выглядеть ужасно в цифрах, и при этом звучать неотличимо от оригинала. В цифровой обработке ...
... несущими и амплитудно-фазовая модуляция с одной боковой полосой (АФМ-ОБП). 3. Выбор длительности и количества элементарных сигналов, используемых для формирования выходного сигнала В реальных каналах связи для передачи сигналов по частотно ограниченному каналу используется сигнал вида , но он бесконечен во времени, поэтому его сглаживают по косинусоидальному закону. , где - ...
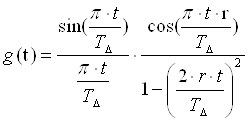
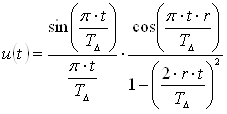
0 комментариев